2020-2021学年第五章 相交线与平行线5.1 相交线5.1.1 相交线练习

这是一份2020-2021学年第五章 相交线与平行线5.1 相交线5.1.1 相交线练习，共35页。试卷主要包含了知识点，考点点拨与训练等内容，欢迎下载使用。

专题5.1 相交线
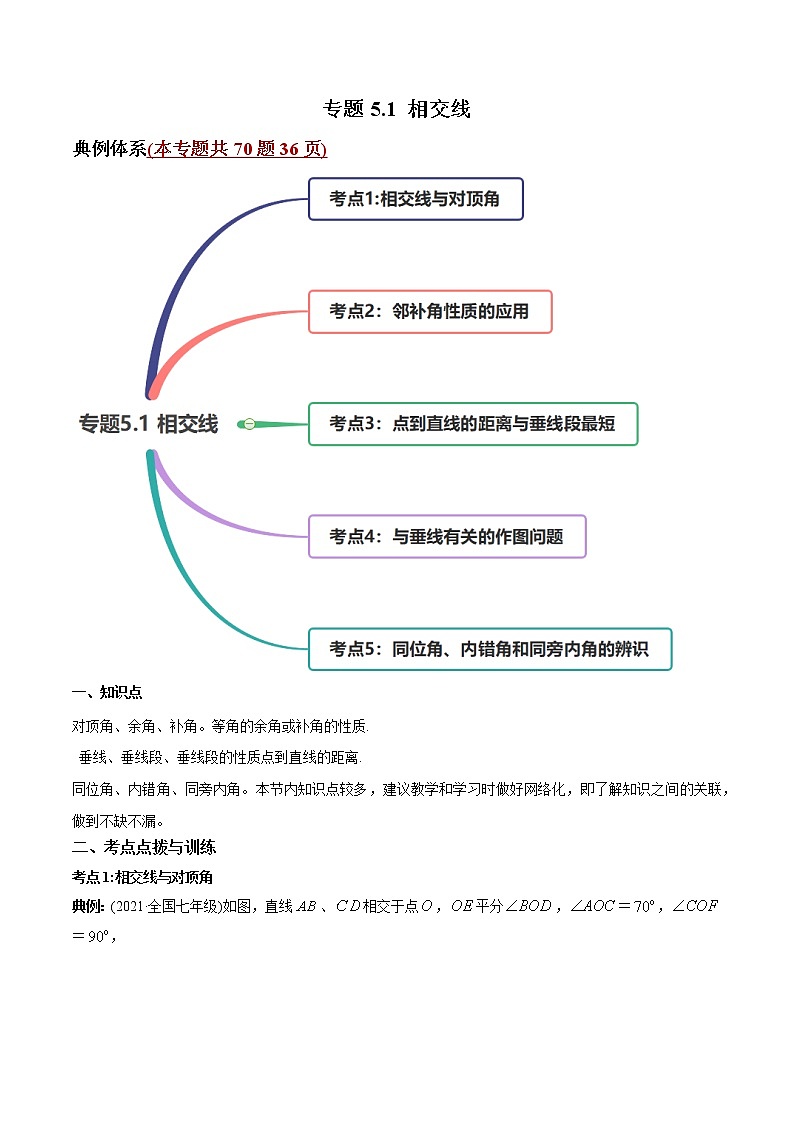
典例体系(本专题共70题36页)

一、知识点
对顶角、余角、补角。等角的余角或补角的性质.
垂线、垂线段、垂线段的性质点到直线的距离.
同位角、内错角、同旁内角。本节内知识点较多，建议教学和学习时做好网络化，即了解知识之间的关联，做到不缺不漏。
二、考点点拨与训练
考点1:相交线与对顶角
典例：(2021·全国七年级)如图，直线、相交于点，平分，＝，＝，

求：(1)的度数；
(2)写出图中互余的角；
(3)的度数．
【答案】(1)70º；(2)和，和，和，和；(3)55º．
【详解】
解：(1)∵＝
∴＝＝；
(2)


平分，


所以互余的角有：和，和，和，和；
(3) 平分，＝
＝，
＝，且、、三点在一条直线上，
＝＝，

方法或规律点拨
此题主要考查了角的和差计算，以及余角，角平分线的定义，关键是掌握余角定义，理清图形中角的关系．
巩固练习
1．(2021·重庆万州区·七年级期末)下列各组角中，∠1与∠2是对顶角的是(　　　)
A． B． C． D．
【答案】B
【详解】
根据两条直线相交，才能构成对顶角进行判断，
A、C、D都不是由两条直线相交构成的图形，错误；
B是由两条直线相交构成的图形，正确．
故选：B．
2．(2020·黑龙江哈尔滨市·七年级期末)在下面四个图形中，与是对顶角的是( )．
A． B．
C． D．
【答案】B
【详解】
解：A、∠1与∠2不是对顶角，故此选项不符合题意；
B、∠1与∠2是对顶角，故此选项符合题意；
C、∠1与∠2不是对顶角，故此选项不符合题意；
D、∠1与∠2不是对顶角，故此选项不符合题意；
故选择：B．
3．(2020·洛阳市第五中学九年级期中)下列说法中，正确的是
A．相等的角是对顶角 B．有公共点并且相等的角是对顶角
C．如果和是对顶角，那么 D．两条直线相交所成的角是对顶角
【答案】C
【详解】
A、对顶角是有公共顶点，且两边互为反向延长线，相等只是其性质，错误；
B、对顶角应该是有公共顶点，且两边互为反向延长线，错误；
C、角的两边互为反向延长线的两个角是对顶角，符合对顶角的定义，正确．
D、两条直线相交所成的角有对顶角、邻补角，错误；
故选C．
4．(2020·福建厦门市·厦门一中七年级期末)如图，直线AB与直线CD相交于点O，其中∠AOC的对顶角是( )

A．∠AOD B．∠BOD C．∠BOC D．∠AOD和∠BOC
【答案】B
【详解】
直线AB与直线CD相交于点O，
由图可知，∠AOC的对顶角是∠BOD，
故选B．
5．(2020·黑龙江哈尔滨市·七年级期末)如图，直线AB、CD相交于点O，OE平分，若，则的度数是( )

A．70° B．50° C．40° D．35°
【答案】D
【详解】∵∠BOD=，
∴∠AOC=∠BOD=，
∵OE平分∠AOC，
∴∠COE=∠AOC=，
故选：D．
6．(2021·北京通州区·七年级期末)如图，两直线交于点，，则的度数为_____________；的度数为_________．

【答案】
【详解】
解：∵
∴=180°-∠1=180°-34°=146°；
∵∠1与∠3互为对顶角
∴∠3=∠1=
故答案为：146°；．
7．(2021·四川宜宾市·七年级期末)如图，已知直线AB和CD相交于O点，∠COE是直角，OF平分∠AOE，∠COF=34º，则∠BOD的度数为____．

【答案】22°
【详解】解：∵∠COE是直角，
∴∠COE＝90°，
∴∠EOF＝∠COE−∠COF＝90°−34°＝56°，
∵OF平分∠AOE，
∴∠AOF＝∠EOF＝56°，
∴∠AOC＝∠AOF−∠COF＝56°−34°＝22°，
∴∠BOD＝∠AOC＝22°．
故答案为：22°．
8．(2020·江西赣州市·七年级期末)∠1的对顶角等于，∠1的余角等于_______________．
【答案】40°
解：∠1的对顶角等于，∠1=，则∠1的余角等于90°-50°=40°．
故答案为：40°．
9．(2020·内蒙古乌兰察布市·七年级期末)如图，取两根木条，将它们钉在一起，并把它们想象成两条直线，就得到一个相交线模型．如果∠1=15°，则∠2=15°，理由是_______________________．

【答案】对顶角相等
【详解】
解：两直线相交，就会有对顶角，对顶角不仅有位置关系，而且有大小关系，即：两直线相交，对顶角相等．
故答案为：对顶角相等．
10．(2019·山西七年级月考)如图，与是对顶角，，，则______．

【答案】40°
【详解】
解：∵∠1与∠2是对顶角，，∠2=50°，
∴∠1=∠2，
∵，∠2=50°，
∴α+10°=50°，
∴α=40°．
故答案为：40°．
11．(2021·河南漯河市·七年级期末)如图，直线，相交于点，平分．

(1)若，求的度数；
(2)若，求的度数．
【答案】(1)；(2)
【详解】平分，
，
；
设，则,，
，
解得，
则，
又平分，
，
．
12．(2020·山东日照市·七年级期末)如图，直线，相交于点，平分．
(1)的补角是____________；
(2)若，求的度数．

【答案】(1)∠AOD和∠BOC；(2)36°
【详解】
(1)∵+∠AOD=180°，+∠BOC=180°，
∴的补角是：∠AOD和∠BOC，
故答案是：∠AOD和∠BOC；
(2)设∠EOC=2x，∠EOD=3x，
根据题意得：2x+3x=180°，
解得：x=36°，
∴∠EOC=2x=72°，
∵平分，
∴∠AOC=∠EOC=×72°=36°，
∴∠BOD=∠AOC=36°．
考点2：邻补角性质的应用
典例：(2020·平原县育才中学七年级期中)如图，直线AB、CD、EF相交于点O．
(1)写出∠COE的邻补角；
(2)分别写出∠COE和∠BOE的对顶角；
(3)如果∠BOD=60°，，求∠DOF和∠FOC的度数．

【答案】(1)∠COF和∠EOD；(2)∠COE和∠BOE的对顶角分别为∠DOF和∠AOF；(3)∠DOF= 30°，∠FOC=150°
【详解】
(1)∠COE的邻补角有∠COF和∠EOD；
(2)∠COE的对顶角为∠DOF，∠BOE的对顶角为∠AOF；
(3)∵，
∴∠BOF=90°，
∴∠DOF= 90°-60°=30°，
∵∠DOF与∠FOC互为邻补角，
∴∠FOC=180°-30°=150°．
方法或规律点拨
本题考查邻补角、对顶角及余角和补角之间的关系，关键是理解并掌握互余、互补、邻补角、对顶角之间的角度和位置关系．
巩固练习
1．(2020·山东潍坊市·七年级期中)把一张长方形纸片沿翻折后，点，分别落在、的位置上，交于点， 则图中与互补的角有( )

A．1个 B．2个 C．3个 D．4个
【答案】C
【详解】∵将长方形纸片沿翻折得到如上图形
∴∠FEG=∠FEC，∠EFD=∠EF
由图形知，∠FEC与∠FCB互补
∵AD∥BC，∴∠FEC与∠EFD互补
∴∠EF与∠EFD也互补
故选：C
2．(2020·全国七年级课时练习)如图所示，，的邻补角是( )，的余角一定是( )．

A．；
B．和；
C．；
D．和；和
【答案】D
【详解】
解：∵EF⊥DC，
∴∠EOD=90°
∴∠AOE+∠AOD=90°
∵∠AOD=∠BOC
∴∠AOE+∠BOC=90°
∴∠AOE的余角是∠AOD，∠BOC；
∵∠AOE+∠AOF =180°，∠AOE+∠BOE=180°，且符合邻补角的定义
∴∠AOE的邻补角是∠AOF，∠BOE；
故选：D．
3．(2020·全国七年级课时练习)如图所示，三条直线AB，CD，EF相交于点O，则的邻补角有( )

A．1个 B．2个 C．3个 D．4个
【答案】B
【详解】
因为构成的两边与直线AB和EF有关，从直线AB来看，的邻补角是，从直线EF来看，的邻补角是，所以的邻补角有2个，故选B.
4．(2019·湖北恩施土家族苗族自治州·七年级月考)如图，直线 AB，CD 交于点 O，则图中互为补角的角对数有( )

A．1 对 B．2 对 C．3 对 D．4 对
【答案】D
【详解】根据图形可得，∠2与∠3互为补角；∠3与∠1互为补角；∠1与∠DOB互为补角；∠2与∠DOB互为补角；共4对．
故选：D．
5．(2019·福州三牧中学七年级期中)如图，已知∠1+∠3=180°，则图中有标出来的角中与∠1互补的角有( )

A．4个 B．3个 C．2个 D．1个
【答案】A
【详解】
解：①与∠1互为邻补角的角有∠5与∠7；
②∠3及∠3的对顶角有∠3与∠4．
所以图中有标出来的角中与∠1互补的角有4个．
故选A．
6．(2020·奈曼旗新镇中学七年级期中)如图，直线AB，CD，EF相交于点O，∠AOC的邻补角是___________．若∠AOC＝50°，则∠BOD＝________，∠COB＝________．

【答案】∠AOD、∠BOC 50° 130°
【详解】
解：∠AOC的邻补角是∠BOC，∠AOD；
∵∠BOD的对顶角是∠AOC，∠AOC＝50°，
∴∠BOD＝∠AOC＝50°，
∵∠COB是∠AOC邻补角，
∴∠COB=180°-∠AOC=130°．
故答案为：∠AOD、∠BOC，50°，130°
7．(2019·山西七年级月考)已知4条直线交于一点，那么邻补角的对数是______对．
【答案】24
【详解】
2条直线相交于一点，邻补角有4对；
3条直线相交于一点，邻补角有12对，
n条直线相交于一点，邻补角有2n(n－1)对，
∴4条直线相交于一点时，共有邻补角：2×4×(4－1)＝24(对)；
故答案为：24．
8．(2019·天津滨海新区·七年级期末)如图，直线AB、CD相交于点O，下列描述：①∠1和∠2互为对顶角；②∠1和∠2互为邻补角；③∠1＝∠2；④∠1＝∠3；⑤∠1+∠4＝180°，其中正确的是_____．

【答案】②④⑤．
【详解】∠1和∠2是邻补角，不是对顶角，故①错误；
∠1和∠2互为邻补角，故②正确；
∠1和∠2不一定相等，故③错误；
∠1和∠3是对顶角，所以，故④正确；
∠1和∠4是邻补角，所以 ，故⑤正确；
故答案为：②④⑤．
9．(2019·全国七年级单元测试)三条直线AB、CD、EF相交于点O，如图所示，∠AOD的对顶角是_____，∠FOB的对顶角是_______，∠EOB的邻补角是________

【答案】∠BOC ∠AOE ∠AOE和∠BOF
【解析】
对顶角和邻补角在两条直线相交的上形中产生，根据对顶角、邻补角的定义得：
∠AOD的对顶角是∠BOC，
∠FOB的对顶角是∠AOE，
∠EOB的邻补角是∠AOE和∠BOF．
故答案为(1)∠BOC (2)∠AOE (3)∠AOE和∠BOF
10．(2020·全国七年级课时练习)如图，直线AB，CD，EF相交于点O，则∠AOD的对顶角是_________，∠AOC的邻补角是_______．若∠AOC＝50°，则∠BOD＝__________，∠COB＝______________．

【答案】∠BOC ; ∠AOD，∠BOC; 50°; 130°.
【详解】
∵AB，CD，EF相交于点O
∴∠AOD的对顶角是∠BOC，
∠AOC的邻补角是∠AOD，∠BOC
∵∠AOC＝50°
∴∠BOD＝50°(对顶角相等)
∠COB＝180°−∠AOC= 180°−50°=130°
11．(2018·全国)如图，直线AB、CD、EF相交于点O，则∠AOC的对顶角是_____________，∠AOE的邻补角是_____________

【答案】∠BOD； ∠AOF、∠BOE.
【详解】
由图可知，∠AOC的对顶角是∠BOD，
∠AOE的邻补角是∠AOF、∠BOE，
故答案为∠BOD；∠AOF、∠BOE.
12．(2019·四川泸州市·七年级期末)如图，直线、与相交于点，形成了个角．

(1)图中，与有一条公共边，它们的另一边互为反向延长线，具有这种关系的两个角，互为邻补角．这样的邻补角还有以下几对，它们分别是____________、__________、______________．
(2)图中，与有一个公共顶点，且的两边分别是的反向延长线，具有这种位置关系的两个角，互为对顶角．这样的对顶角还有一对，它们是________与___________．
(3)因为______________，____________所以______(填写或或)理由是____________由此能得到的结论是：对顶角_____________
(4)用您所学知识可得___________(精确到度)．
【答案】(1)∠AOD与∠BOD；∠AOC与∠BOC；∠BOD与∠BOC；(2)∠AOD；∠BOC；(3)180°；180°；=；同角的补角相等；相等；(4)45°
【详解】(1)图中的邻补角还有：∠AOD与∠BOD；∠AOC与∠BOC；∠BOD与∠BOC
故答案为：∠AOD与∠BOD；∠AOC与∠BOC；∠BOD与∠BOC
(2)这样的对顶角还有一对，它们是∠AOD与∠BOC；
故答案为：∠AOD；∠BOC
(3)因为180°，180°，所以=，理由是：同角的补角相等，由此能得到的结论是：对顶角相等．
故答案为：180°；180°；=；同角的补角相等；相等
(4)经测量∠COA=45°
考点3：点到直线的距离与垂线段最短
典例：(2020·湖南娄底市·)如图，是直线外一点，，，三点在直线上，且于点，，则下列结论：①线段是点到直线的距离；②线段的长是点到直线的距离；③，，三条线段中，最短；④线段的长是点到直线的距离．其中正确的是( )

A．②③ B．①②③ C．③④ D．①②③④
【答案】A
【详解】
解：①线段AP是点A到直线PC的距离，错误；
②线段BP的长是点P到直线l的距离，正确；
③PA，PB，PC三条线段中，PB最短，正确；
④线段PC的长是点P到直线l的距离，错误，
故选：A．
方法或规律点拨
此题主要考查了垂线的两条性质：①从直线外一点到这条直线的垂线段的长度，叫做点到直线的距离．②从直线外一点到这条直线上各点所连的线段中，垂线段最短．
巩固练习
1．(2021·北京海淀区·北大附中七年级期末)如图，从直线EF外一点P向EF引四条线段PA，PB，PC，PD，其中最短的是( )

A．PA B．PB C．PC D．PD
【答案】B
【详解】从直线EF外一点P向EF引四条线段PA，PB，PC，PD，其中最短的一条是PB，
故选：B．
2．(2021·北京通州区·七年级期末)如图，是直线外一点，从点向直线引，，，几条线段，其中只有与垂直，这几条线段中长度最短的是(　　　)

A． B． C． D．
【答案】B
【详解】
解：直线外一点 P 与直线上各点连接的所有线段中，最短的是 PB ，依据是垂线段最短．
故答案选B．
3．(2021·北京顺义区·七年级期末)如图，点在直线外，点、在直线上，若，，则点到直线的距离可能是( )

A．3 B．4 C．5 D．7
【答案】A
【详解】
如图作⊥直线于，
∴为点到直线的距离，
∵，，
∴，
∴只有A选项符合题意，
故选：A．

4．(2020·沭阳县修远中学七年级月考)如图，建筑工人砌墙时，经常在两个墙脚的位置分别插一根木桩，然后拉一条直的参照线，其运用到的数学原理是( )

A．两点之间，线段最短 B．两点之间线段的长度，叫做这两点之间的距离
C．垂线段最短 D．两点确定一条直线
【答案】D
【详解】
解：建筑工人砌墙时，经常在两个墙脚的位置分别插一根木桩，然后拉一条直的参照线，这种做法运用到的数学原理是：两点确定一条直线．
故选：D．
5．(2020·黑龙江大庆市·七年级期末)如图，点是直线外一点，，，，都在直线上，于，下列线段最短的是( )

A． B． C． D．
【答案】C
【详解】
因为点是直线外一点，，，，都在直线上，于，
所以，根据垂线段的性质可知：线段最短．
故选：C．
6．(2021·全国八年级)如图，从旗杆AB的顶端A向地面拉一条绳子，绳子底端恰好在地面P处，若旗杆的高度为3.2米，则绳子AP的长度不可能是(　　)

A．3 B．3.3 C．4 D．5
【答案】A
【详解】
∵旗杆的高度为AB＝3.2米，
∴AP＞AB，
∴绳子AP的长度不可能是：3米．
故选择：A．
7．(2020·大庆市万宝学校八年级期中)下列说法中，正确的是( )
A．在同一平面内，过一点有无数条直线与已知直线垂直
B．两直线相交，对顶角互补
C．垂线段最短
D．直线外一点到这条直线的垂线段叫做点到直线的距离
【答案】C
【详解】
解：A．在同一平面内，过一点有且仅有一条直线与已知直线垂直，故本选项错误；
B．两直线相交，对顶角相等，故本选项错误；
C．垂线段最短，故本选项正确；
D．直线外一点到这条直线的垂线段的长度叫做点到直线的距离，故本选项错误；
故选：C．
8．(2019·河北保定市·七年级期中)如图，立定跳远比赛时，小明从点A起跳落在沙坑内P处．若AP＝2.3米，则这次小明跳远成绩

A．小于2.3米 B．等于2.3米
C．大于2.3米 D．不能确定
【答案】A
【详解】
如图，过点P作PE⊥AC，垂足为E，
∴PE ∵PA=2.3米，
∴这次小明跳远成绩小于2.3米，
故选A.

9．(2019·河北唐山市·七年级期中)如图，某地进行城市规划，在一条新修公路旁有一超市，现要建一个汽车站，且有四个地点可供选择．若要使超市距离汽车站最近，则汽车站应建在( )

A．点处 B．点处 C．点处 D．点处
【答案】C
【详解】
解：直线外一点到直线上的所有连线中，垂线段最短，
故选：C．
10．(2018·山东济南市·七年级期中)下列图形中，线段的长表示点到直线距离的是( )．
A． B． C． D．
【答案】D
【详解】
结合题意，线段的长表示点到直线距离的为：

故选：D．
11．(2020·海伦市第三中学七年级期中)点P是直线l外一点，A为垂足，，且，则点P到直线l的距离( )
A．小于 B．等于 C．大于 D．不确定
【答案】B
【详解】
解：根据点到直线的距离的定义得出P到直线l的距离是等于，
故选：B．
12．(2019·山西七年级月考)如图，在中，，于点，则图中能表示点到直线的距离的是( )

A．的长度 B．的长度 C．的长度 D．的长度
【答案】B
【详解】
由在中，，于点，可得：
能表示点到直线的距离的是BC的长度；
故选B．
13．(2020·吉林长春市·七年级期末)如图，在中，于点，点到直线的距离是( )

A．线段的长 B．线段的长
C．线段的长 D．线段的长
【答案】C
【详解】
解：因为于点，所以AD的长即为点A到直线BC的距离；
故选C．
14．(2020·河南信阳市·七年级期中)下列图形中，线段PQ的长度表示点P到直线L的距离的是( )
A． B． C． D．
【答案】C
【详解】
A. PQ不垂直于直线l，故不符合题意，
B. PQ不垂直于直线l，故不符合题意，
C. PQ⊥l，即：线段PQ的长度表示点P到直线l的距离，故符合题意，
D. PQ不垂直于直线l，故不符合题意，
故选C．
15．(2019·四川凉山彝族自治州·七年级期末)下列作图能表示点A到BC的距离的是(　　)

A．A B．B C．C D．D
【答案】B
【详解】
解：A.BD表示点B到AC的距离，故A选项错误；
B. AD表示点A到BC的距离，故B选项正确； 
C. AD表示点D到AB的距离，故C选项错误； 
D. CD表示点C到AB的距离，故D选项错误； 
故选B．
16．(2020·长白朝鲜族自治县宝泉山镇中学七年级期末)下列图形中线段PQ的长度表示点P到直线a的距离的是(　　)
A． B．
C． D．
【答案】C
【详解】
解：由题意得PQ⊥a，
P到a的距离是PQ垂线段的长，
故选：C．
17．(2019·贵州铜仁市·七年级期末)下列图形中，线段的长表示点到直线的距离是( )
A． B．
C． D．
【答案】A
【详解】
解：利用点到直线的距离的定义可知：线段PQ的长表示点P到直线MN的距离的是A选项．
故选：A．
18．(2020·湖北襄阳市·七年级期末)如图，，于点D，点C到AD的距离是下列哪条线段的长度   

A．AC B．BC C．CD D．AD
【答案】C
【详解】
∵，
∴，
∴点C到AD的距离是线段CD的长度．
故答案选C．
19．(2021·北京海淀区·人大附中七年级期末)如图是小明同学在体育课上跳远后留下的脚印，那么体育陈老师测量小明同学的体育成绩，应该选取线段____________的长度，其依据是_______________．

【答案】CD 垂线段最短
【详解】
在跳远比赛规则的前提下，测量小明同学的体育成绩时，应该选取线段CD的长度，其依据是垂线段最短，
故答案为：CD、垂线段最短．
考点4：与垂线有关的作图问题
典例：(2021·北京房山区·七年级期末)已知，如图，点、分别代表两个村庄，直线代表两个村庄之间的一条燃气管道，根据村民燃气需求，计划在管道上某处修建一座燃气管理站，向两村庄接入管道．
(1)若计划建一个离村庄最近的燃气管理站，请画出燃气管理站的位置(用点表示)，这样做的依据是________________________________________．
(2)若考虑到管道铺设费用问题，希望燃气管理站的位置到村庄、村庄距离之和最小，画出燃气管理站的位置(用点表示)，这样做的依据是___________________________．

【答案】(1)画图见详解，垂线段最短；(2)画图见详解，两点之间，线段最短．
【详解】
(1)∵计划建一个离村庄最近的燃气管理站，
过点M作MP⊥直线l，
则MP为垂线段，
∴点P为所求，
根据连结直线外一点M，与直线上个点的所有线中，垂线段最短，
故答案为：垂线段最短；

(2)∵燃气管理站的位置到村庄、村庄距离之和最小，
∴连结MN，
∵根据所有连结两点的线中，线段最短，
∴MQ+NQ=MN，
∴点Q为所求．
故答案为：两点之间，线段最短．

方法或规律点拨
本题考查垂线段最短，与两点之间，线段最短问题，掌握垂线段，与线段的定义，会利用垂线段最短，与两点之间，线段最短问题解释生活中实际问题是解题关键．
巩固练习
1．(2021·全国八年级)阅读下面材料：
在数学课上，老师提出如下问题：
如图，需要在A、B两地和公路l之间修地下管道．请你设计一种最节省材料的修路方案：

小丽设计的方案如下：
如图，(1)连接AB；
(2)过点A画线段AC⊥直线l于点C，所以线段BA和线段AC即为所求．

老师说：“小丽的画法正确”
请回答：小丽的画图依据是___．
【答案】两点之间线段最短；直线外一点到这条直线上所有点连结的线段中，垂线段最短(或垂线段最短)
【详解】
由垂线段最短可知，点A到直线l的最短距离为AC，由两点之间线段最短可知，点B到点A的最短距离为AB．
故答案为：两点之间线段最短；直线外一点到这条直线上所有点连结的线段中，垂线段最短(或垂线段最短)；
2．(2021·北京昌平区·七年级期末)如图，已知一条笔直的公路l的附近有A，B，C三个村庄．
(1)画出村庄A，C间距离最短的路线；
(2)加油站D在村庄B，C所在直线与公路l的交点处，画出加油站D的位置；
(3)画出村庄C到公路l的最短路线，作图依据是____________，测量______(精确到)；如果示意图与实际距离的比例尺是1∶200000，通过你的测量和计算，在实际中村庄C到公路l的最短路线为________．

【答案】(1)见解析；(2)见解析；(3)垂线段最短；1.6；3.2；见解析
【详解】解：(1)如图所示．根据两点之间线段最短，连接AC，
(2)如图所示．连接直线BC,直线BC与公路l的交点，即为加油站D，
(3)如图所示．
作图依据：垂线段最短．
过点C作CE⊥l,交点为E,
测量CE，．
∵示意图与实际距离的比例尺是1∶200000
∴CE：实际距离=1：200000
实际距离=200000×1.6=320000cm=3.2km
在实际中村庄C到公路l的最短线路为．

3．(2021·浙江温州市·七年级期末)点A、B、C如图所示，请按要求完成下列问题．

(1)作直线AB，射线AC；
(2)作出点B到射线AC的最短线段BD；
(3)作线段BC，则________BC．(填“>”，“=”或“<”)．
【答案】(1)见解析；(2)见解析；(3)作图见解析，>．
【详解】
(1)如图，直线，射线即为所求；
(2)如图，线段即为所求；
(3)连接，根据两点之间线段最短，可得，
故答案为：>．

4．(2021·江苏连云港市·七年级期末)在如图所示的方格中，每个小正方形的边长为1，点在方格纸中小正方形的顶点上．

(1)画线段；
(2)画图并说理：
①画出点到线段的最短线路，理由是 ；
②画出一点，使最短，理由是 ．
【答案】(1)图见解析；(2)图见解析，点到直线的距离垂线段最短；(3)图见解析，两点之间线段最短．
【详解】
(1)连接AB如下图所示；
(2)①如图所示CE为最短路径，理由是点到直线的距离垂线段最短，
故答案为：点到直线的距离垂线段最短；
②如图所示P点为最短，理由是：两点之间线段最短，
故答案为：两点之间线段最短．

5．(2020·北京七年级期末)如图，已知直线AB及直线AB外一点P，按下列要求完成画图和解答：(1)连接PA，PB，用量角器画出∠APB的平分线PC，交AB于点C；
(2)过点P作PD⊥AB于点D；
(3)用刻度尺取AB中点E，连接PE；
(4)根据图形回答：点P到直线AB的距离是线段 的长度．

【答案】(1)答案见解析；(2)答案见解析；(3)答案见解析；(4)PD．
【详解】
解：(1)、如图所示；(2)、如图所示；(3)、如图所示；

(4)、PD．
6．(2019·洛阳市实验中学七年级月考)作图并填空：如图，在中，点在边上，

(1)过点P分别作直线、直线的垂线，交直线于点；
(2)点P到直线的距离是线段_________的长度；
(3)点O到直线的距离是线段_________的长度．
【答案】(1)图见解析；(2)PN；(3)ON
【详解】
解：(1)过点P分别作直线、直线的垂线，交直线于点，如图所示，PM和PN即为所求；

(2)根据点到直线的距离的定义：点P到直线的距离是线段PN的长
故答案为：PN；
(3)根据点到直线的距离的定义：点O到直线的距离是线段ON的长
故答案为：ON．
7．(2020·宿迁市钟吾初级中学七年级期末)如图，在6×6的正方形网格中，点P是∠AOB的边OB上的一点．

(1)过点P画OB的垂线，交OA于点C；
(2)过点P画OA的垂线，垂足为H；
(3) 的长度是点C到直线OB的距离；
(4)线段PC、PH、OC这三条线段大小关系是 ．(用“<”号连接)
【答案】(1)见解析；(2)见解析；(3)PC；(4)PH＜PC＜OC
【详解】
解：(1)如图所示；
(2)如图所示；
(3)线段PC的长度是点C到直线OB的距离，
故答案为：PC；
(4)根据垂线段最短可得PH＜PC＜OC．

8．(2021·北京延庆区·七年级期末)(1)如图1，平面上有3个点A，B，C．


①画直线AB；画射线BC；画线段AC；
②过点C作AB的垂线，垂足为点D；
③量出点C到直线AB的距离约为 cm．
(2)尺规作图：
已知：线段a，b，如图2．
求作：一条线段MN，使它等于2a－b．(不写作法，保留作图痕迹)
【答案】(1)①见详解；②见详解；③2.3；(2)见详解
【详解】
解：(1)①②如图所示：


③利用直尺可量出点C到直线AB的距离即为线段CD的长，约为2.3cm；
故答案为2.3；
(2)先作一条射线MA，然后利用圆规量出线段a的长，以点M为圆心线段a的长为半径画弧，依次再画出一段a的长，最后交射线MA于点B，进而以点B为圆心，线段b的长为半径画弧，交线段MB于点N，则线段MN即为所求，如图所示：

∴MN=2a-b．
9．(2021·北京门头沟区·七年级期末)如图，已知平面上三点，，，请按要求画图，并回答问题：

(1)画直线AC，射线BA；
(2)延长AB到 D，使得BD=AB，连接CD；
(3)过点C画，垂足为；
(4)通过测量可得，点C到AB所在直线的距离约为________cm(精确到0.1 cm)．
【答案】(1)见详解；(2)见详解；(3)见详解；(4)3.5
【详解】
解：(1)(2)(3)如图所示：

(4)通过直尺进行测量可得点C到AB所在直线的距离约为3.5cm；
故答案为3.5．
考点5：同位角、内错角和同旁内角的辨识
典例：(2020·上海同济大学实验学校七年级期中)如图，共有_____对同位角，有_____对内错角，有_____对同旁内角．

【答案】20 12 12
【详解】
解：同位角：∠AEO和∠CGE，∠OEF和∠EGH，∠OFB和∠OHD，∠OFE和∠OHG，∠IGH和∠IEF，∠AEI和∠CGI，∠AFJ和∠CHJ，∠DHJ和∠JFB，∠AEO和∠AFO，∠OEB和∠OFB，∠AEG和∠AFH，∠GEB和∠HFB，∠EGH和∠OHD，∠OGC和∠OHC，∠O与∠EFH，∠O与∠GEF，∠O和∠IGH，∠O和∠GHJ，
∠CGI和∠CHJ，∠HGI和∠DHJ，共20对；
内错角：∠O和∠OEA，∠O和∠OFB，∠O和∠OGC，∠O和∠OHD，∠AEG和∠EGH，∠BEG和∠EGC，∠BFH和∠FHC，∠AFH和∠FHD，∠OEF和∠EFH，∠GEF和∠OFE，∠OGH和∠GHJ，∠OHG和∠IGH，共12对；
同旁内角：∠OEF和∠O，∠OFE和∠O，∠O和∠OGH，∠O和∠OHC，∠OEF和∠OFE，∠OGH和∠OHG，∠GEF和∠EFH，∠IGH和∠GHJ，∠AEG和∠CGE，∠BFH和∠FHD，∠FEG和∠EGH，∠EFH和∠GHF，共12对，
故答案为：20；12；12．
方法或规律点拨
此题主要考查了同位角、内错角、同旁内角，关键是掌握同位角的边构成“F”形，内错角的边构成“Z”形，同旁内角的边构成“U”形．
巩固练习
1．(2020·浙江杭州市·七年级其他模拟)如图，和不是同位角的是( )
A． B． C． D．
【答案】C
【详解】
解：A、∠1和∠2是同位角，故此选项不符合题意；
B、∠1和∠2是同位角，故此选项不符合题意；
C、∠1和∠2不是同位角，故此选项符合题意；
D、∠1和∠2是同位角，故此选项不符合题意；
故选C．
2．(2020·浙江金华市·七年级期末)如图，的同位角是(　　　)

A． B． C． D．
【答案】A
【详解】
解：两条直线被第三条直线所截，在截线的同旁，被截两直线的同一侧的角，我们把这样的两个角称为同位角．即∠2是∠1的同位角．
故选：A．
3．(2020·长汀县第四中学七年级月考)如图所示，下列结论中正确的是( )

A．∠1和∠2是同位角 B．∠1和∠4是内错角
C．∠2和∠3是同旁内角 D．∠3和∠4是对顶角
【答案】C
【详解】
解：A、∠1和∠2是同旁内角，故本选项错误；
B、∠1和∠4是同位角，故本选项错误；
C、∠2和∠3是同旁内角，故本选项正确；
D、∠3和∠4是邻补角，故本选项错误；
故选：C．
4．(2020·黑龙江哈尔滨市·七年级期末)如图，和不是同旁内角的是( )
A． B． C． D．
【答案】D
【详解】
解：选项A、B、C中，∠1与∠2在两直线的之间，并且在第三条直线(截线)的同旁，是同旁内角，故不符合题意；
选项D中，∠1与∠2的两条边都不在同一条直线上，不是同旁内角，符合题意．
故选：D．
5．(2020·重庆沙坪坝区·七年级期末)如图，下列说法错误的是(　　)

A．∠1与∠3是对顶角 B．∠3与∠4是内错角
C．∠2与∠6是同位角 D．∠3与∠5是同旁内角
【答案】C
【详解】
A、∠1与∠3是对顶角，故A说法正确；
B、∠3与∠4是内错角，故B说法正确；
C、∠2与∠6不是同位角，故C说法错误；
D、∠3与∠5是同旁内角，故D说法正确；
故选：C．
6．(2021·全国七年级)如图，直线和被直线所截，则(　　　)

A．和是同位角 B．和是内错角
C．和是同位角 D．和是内错角
【答案】C
【详解】
同位角是位于两直线及截线的同侧，内错角是位于两直线内侧及截线两侧，故和是同位角；
故选：C．
7．(2020·上海市民办立达中学七年级月考)如图，∠1与∠2是( )

A．同位角 B．内错角 C．同旁内角 D．以上都不对
【答案】D
【详解】
解：同位角，内错角，同旁内角都只涉及到三条线(直线或射线或线段)．
∠1与∠2共涉及到四条线(直线或射线或线段)，不满足“三线八角”的概念．
故选：D．
8．(2021·全国七年级)下列所示的四个图形中，∠1和∠2是同位角的是( )

A．②③ B．①②③
C．①②④ D．①④
【答案】C
【详解】
解：图①、②、④中，∠1与∠2在截线的同侧，并且在被截线的同一方，是同位角；
图③中，∠1与∠2的两条边都不在同一条直线上，不是同位角．
故选：C．
9．(2019·黑龙江绥化市·八年级期末)下列图形中，∠1与∠2不是同位角的是( )
A． B． C． D．
【答案】B
【详解】
解：观察A、B、C、D，四个答案，A、C、D都是“F”形状的，而B不是．
故选：B
10．(2019·甘肃庆阳市·七年级期中)下列所示的四个图形中，∠1和∠2是同位角的是( )

A．②③ B．①②③ C．①②④ D．①④
【答案】C
【详解】
图①中的∠1与∠2是同位角，
图②中的∠1与∠2是同位角，
图③中的∠1与∠2不是同位角，
图④中的∠1与∠2是同位角，
所以在如图所示的四个图形中，图①②④中的∠1和∠2是同位角．
故选：C．
11．(2019·山西七年级月考)如图，直线，被直线所截，则与是( )

A．同位角 B．内错角 C．同旁内角 D．对顶角
【答案】A
【详解】
解：直线a，b被直线c所截，∠1与∠2是同位角．
故选：A．
12．(2021·全国七年级)分别指出下列图中的同位角、内错角、同旁内角．

【答案】图1中同位角有：∠1与∠5，∠2与∠6，∠3与∠7，∠4与∠8；内错角有：∠3与∠6，∠4与∠5；同旁内角有：∠3与∠5，∠4与∠6.；图2中同位角有：∠1与∠3，∠2与∠4；同旁内角有：∠3与∠2．
【详解】
解：如图1，

同位角有：∠1与∠5，∠2与∠6，∠3与∠7，∠4与∠8；
内错角有：∠3与∠6，∠4与∠5；
同旁内角有：∠3与∠5，∠4与∠6．
如图2，
同位角有：∠1与∠3，∠2与∠4；
同旁内角有：∠3与∠2．
13．(2020·浙江杭州市·七年级其他模拟)如图，与是同位角的是__________．

【答案】①②
【详解】
解：这四个图中，∠1与∠2有一条边在同一条直线上，另一条边在被截线的同一方，是同位角，符合的有图①②．
故答案为：①②．