2021年山东省烟台市莱州市七年级上学期数学期末试卷及答案

七年级上学期数学期末试卷

一、单项选择题

1.以下各数中，为无理数的是〔    〕           

A.                         B.                                        C.                                        D. 

2.以下数据能确定物体具体位置的是〔    〕           

A. 明华小区东        B. 希望路右边                   C. 东经118°，北纬28°                   D. 北偏东30°

3.以下图象中，不表示y是x的函数的是〔    〕           

A.    B.      C.      D. 

4.以下各组条件中，不能判定 的是〔    〕           

A.               B. 
C.                 D. 

5.化简 的结果正确的选项是〔    〕           

A.                   B.                               C.                               D. 

6.点P的坐标是〔3，-1〕，那么点P关于x轴的对称点坐标在〔　　〕           

A. 第一象限             B. 第二象限                           C. 第三象限                           D. 第四象限

7.如下图的图案是由两个直角三角形和三个正方形组成的图形，其中一直角三角形的斜边和一直角边长分别是13，12，那么阴影局部的面积是〔    〕 

A. 25                          B. 16                                         C. 50                                         D. 41

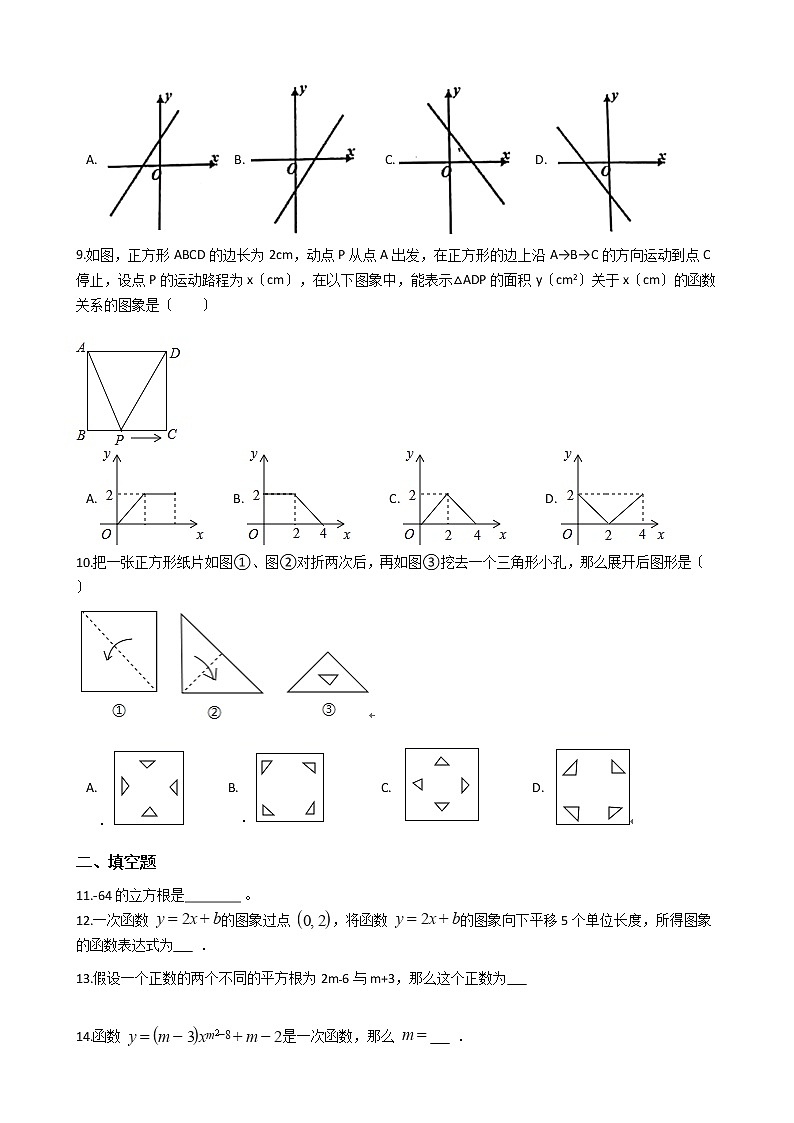
8.正比例函数 〔 〕的函数值y随x的增大而减小，那么一次函数 的图象大致是〔    〕           

A.    B.       C.       D. 

9.如图，正方形ABCD的边长为2cm，动点P从点A出发，在正方形的边上沿A→B→C的方向运动到点C停止，设点P的运动路程为x〔cm〕，在以下图象中，能表示△ADP的面积y〔cm2〕关于x〔cm〕的函数关系的图象是〔　　〕

A.         B.            C.            D. 

10.把一张正方形纸片如图①、图②对折两次后，再如图③挖去一个三角形小孔，那么展开后图形是〔   〕 

A.       B.            C.            D. 

二、填空题

11.-64的立方根是________ 。   

12.一次函数 的图象过点 ，将函数 的图象向下平移5个单位长度，所得图象的函数表达式为       ．   

13.假设一个正数的两个不同的平方根为2m﹣6与m+3，那么这个正数为       

14.函数 是一次函数，那么        ．   

15.点 在直线 上，那么a=       ．   

16.点A的坐标为 ，以点A为圆心，5个单位长度为半径画圆，与y轴的交点坐标为       ．   

17.如图， 中， 是 的垂直平分线， ， 的周长为 ， 那么 的周长为       ．  

18.如图，点 和 都在直线 上，比拟大小：        ． 

19.如图，长方体的底面边长分别为1cm和3cm，高为6cm．如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B，那么所用细线最短需要      cm．

20.假设用初中数学课本上使用的科学计算器进行计算，那么以下按键的结果为       ．

21.点 ．   

〔1〕假设点P在y轴上，P点的坐标为________．   

〔2〕假设点P的纵坐标比横坐标大6，那么点P在第________象限．   

〔3〕假设点P在过点 且与x轴平行的直线上，那么点P的坐标为________．   

〔4〕点P到x轴、y轴的距离相等，那么点P的坐标为________．   

三、解答题

22.计算： ．   

23.在如下图的正方形网格中，每个小正方形的边长为1，格点三角形〔顶点是网格线的交点的三角形〕ABC的顶点A，C的坐标分别为〔 ，5〕，〔 ，3〕.

⑴请在如下图的网格平面内作出平面直角坐标系；

⑵请作出△ABC关于y轴对称的△A′B′C′；

⑶写出点B′的坐标.

24.如图，方格纸中每个小方格的边长为1，在方格纸内作一个面积为5的等腰直角三角形． 

25.假设 都是实数，且 ，求 x＋3y的立方根。   

26.如图，在 中， ． 和 的平分线相交于点F， 交 于点D， 交 于点E．求 的周长． 

27.如图，在平面直角坐标系中，一次函数 与x轴交于点A，与y轴交于点 ，与正比例函数 交于点 ． 

〔1〕求直线 的函数表达式；   

〔2〕点P是直线 上的一点，假设 的面积为4，求点P的坐标．   

28.如图，在 中， ， ，D是 的中点， 交 于点G，E为线段 上任意一点，点F在线段 上，且 ，连结 与 ，过点F作 ，交直线 于点H． 

〔1〕试说明 的理由；   

〔2〕判断 与 的数量关系，并说明理由．   

29.甲、乙两人方案8：00一起从学校出发，乘坐班车去博物馆参观，乙乘坐班车准时出发，但甲临时有事没赶上班车，8：45甲沿相同的路线自行驾车前往，结果比乙早1小时到达.甲、乙两人离学校的距离y〔千米〕与甲出发时间x〔小时〕的函数关系如下图.

〔1〕点A的实际意义是什么？   

〔2〕求甲、乙两人的速度；   

〔3〕求OC和BD的函数关系式；   

〔4〕求学校和博物馆之间的距离.   

答案解析局部

一、单项选择题

1.【解析】【解答】解：A、 ，2是整数，属于有理数，故此选项不符合题意；

B、 ，2是整数，属于有理数，故此选项不符合题意；

C、 是分数，属于有理数，故此选项不符合题意；

D、 属于无理数，故此选项符合题意．

故答案为：D．

【分析】无理数是无限不循环小数，根据无理数的定义进行判断即可。

2.【解析】【解答】解：明华小区东、希望路右边、北偏东30°都不能确定物体的具体位置，

东经118°，北纬28°能确定物体的具体位置，

故答案为：C．

【分析】根据确定物体位置的方法对每个选项一一判断即可。

3.【解析】【解答】解：A、根据图象知给自变量一个值，可能有2个函数值与其对应，故A选项不是函数，

 B、根据图象知给自变量一个值，有且只有1个函数值与其对应，故B选项是函数，

 C、根据图象知给自变量一个值，有且只有1个函数值与其对应，故C选项是函数，

 D、根据图象知给自变量一个值，有且只有1个函数值与其对应，故D选项是函数，

故答案为：A．

【分析】 对于两个变量x和y，如果每给定x的一个值，y都有唯一一个确定的值与其对应，那么我们就说y是x的函数 。根据函数的定义对每个选项进行判断求解即可。

4.【解析】【解答】解：A、根据SAS即可判定全等，该项不符合题意；

B、根据SSA不能判定全等，该项符合题意；

C、根据SAS即可判定全等，该项不符合题意；

D、根据ASA即可判定全等，该项不符合题意；

故答案为：B．

【分析】根据全等三角形的判定方法对每个选项一一判断求解即可。

5.【解析】【解答】解：∵ ，

∴ =-( )= ，

故答案为：D．

【分析】先求出，再利用负数的绝对值是它的相反数，进行计算求解即可。

6.【解析】【解答】解：∵点P的坐标是〔3，-1〕，

∴点P关于x轴的对称点坐标为 ，

∴点在第一象限；

故答案选A．

【分析】先求出点P关于x轴的对称点坐标为 ，再进行判断即可。

7.【解析】【解答】解：

由勾股定理得，

阴影局部的面积是 ，

故答案为：C．

【分析】利用勾股定理求出AB2=25，再求阴影局部的面积即可。

8.【解析】【解答】解：∵正比例函数y随x的增大而减小，

∴ ，那么

函数 中，

∴函数图象经过一、二、三象限

故答案为：A．

【分析】先求出， 再根据2＞0，进行求解即可。

9.【解析】【解答】解：当P点由A运动到B点时，即0≤x≤2时，y= ×2x=x，

当P点由B运动到C点时，即2＜x＜4时，y= ×2×2=2，

符合题意的函数关系的图象是A；

应选：A．

【分析】△ADP的面积可分为两局部讨论，由A运动到B时，面积逐渐增大，由B运动到C时，面积不变，从而得出函数关系的图象．此题考查了动点函数图象问题，用到的知识点是三角形的面积、一次函数，在图象中应注意自变量的取值范围．

10.【解析】【解答】解：当正方形纸片两次沿对角线对折成为一直角三角形时，在直角三角形中间的位置上剪三角形，那么直角顶点处完好，即原正方形中间无损，且三角形关于对角线对称，三角形的一个顶点对着正方形的边.
故答案为：C.
【分析】结合空间思维，分析折叠的过程以及所剪三角形的位置，结合图形对称性可得结果。

二、填空题

11.【解析】【解答】∵〔-4〕3=-64，
∴ -64的立方根是-4.
【分析】根据立方根的定义进行解答即可.

12.【解析】【解答】解：∵一次函数y=2x+b的图象过点〔0，2〕，

∴b=2，

∴一次函数为y=2x+2，

将函数y=2x+2的图象向下平移5个单位长度，所得函数的解析式为y=2x+2-5，即y=2x-3．

故答案为：y=2x-3．

【分析】先求出b=2，再求出一次函数解析式为y=2x+2，最后根据平移的性质进行求解即可。

13.【解析】【解答】解：∵一个正数的两个不同的平方根为2m﹣6与m+3，

∴2m﹣6+m+3=0，

m=1，

∴2m﹣6=﹣4，

∴这个正数为：〔﹣4〕2=16，

故答案为：16

【分析】根据题意得出方程，求出方程的解即可．

14.【解析】【解答】解：依题意得：m2-8=1且m-3≠0， 

解得m=-3． 

故答案为：-3．

【分析】根据一次函数的定义求出m2-8=1且m-3≠0， 再计算求解即可。

15.【解析】【解答】解：∵点 在一次函数 直线上，

∴ ，

解得 ，

故答案为：-8．

【分析】将点A的坐标代入可得，再计算求解即可。

16.【解析】【解答】解：设圆与y轴的交点为B，C，如下图：

∵点A的坐标为 ，以点A为圆心，5个单位长度为半径画圆，

∴OA=3，AB=5，

∴在直角三角形OAB中，OB= ，

∴B〔0，4〕，

同理：C〔0，-4〕．

故答案是： ， ．

【分析】先求出OA=3，AB=5，再利用勾股定理求出OB=4，最后求点的坐标即可。

17.【解析】【解答】解：∵DE是AC的中垂线，

∴AD=CD，

∴△ABD的周长=AB+BD+AD=AB+BD+CD=AB+BC=18，

又∵AE=5cm，

∴AC=2AE=2×5=10cm，

∴△ABC的周长= AB+BC +AC =18+10=28cm，

故答案是：28cm．

【分析】先求出AD=CD，再求三角形的周长即可。

18.【解析】【解答】解：∵直线 经过第二、三、四象限，

∴k＜0，

∴y随x的增大而减小，

∵−4＜−2，

∴y1＞y2 ．

故答案为：＞．

【分析】先求出k＜0，再求出y随x的增大而减小，即可作答。

19.【解析】【解答】解：将长方体展开，连接A、B′，

∵AA′=1+3+1+3=8〔cm〕，A′B′=6cm，

根据两点之间线段最短，AB′= =10cm．

故答案为：10．

【分析】要求细线的长度最短，根据两点之间线段最短，因此将长方体展开，连接AB′，求出AA′，A′B′的长，再利用勾股定理求出AB′即可。

20.【解析】【解答】

解：原式=4﹣9、﹣5，

故答案为：﹣5．

【分析】此题就是计算-， 先算开方运算，再算减法运算即可得出答案。

21.【解析】【解答】解：〔1〕∵点P在y轴上，

∴2m-6=0，

解得m=3，

∴P点的坐标为〔0，5〕；

故答案为〔0，5〕；

〔2〕根据题意得2m-6+6=m+2，

解得m=2，

∴P点的坐标为〔-2，4〕，

∴点P在第二象限；

故答案为：二；

〔3〕∵点P在过A〔2，3〕点且与x轴平行的直线上，

∴点P的纵坐标为3，

∴m+2=3，

∴m=1，

∴点P的坐标为〔-4，3〕．

故答案为：〔-4，3〕；

〔4〕∵点P到x轴、y轴的距离相等，

∴2m-6=m+2或2m-6+ m+2=0，

∴m=8或m= ，

∴点P的坐标为 或 ．

【分析】根据点 和题意进行求解即可。

三、解答题

22.【解析】【分析】利用立方根和二次根式的性质与化简进行计算求解即可。

23.【解析】【分析】〔1〕易得y轴在C的右边一个单位，x轴在C的下方3个单位；〔2〕作出A，B，C三点关于y轴对称的三点，顺次连接即可；〔3〕根据所在象限及距离坐标轴的距离可得相应坐标.

24.【解析】【分析】先求出 ，再利用勾股定理作图求解即可。

25.【解析】【分析】
根据被开方数大于等于0列式求出x的值，然后求出y的值，代入代数式求解，再根据立方根的定义解答。

26.【解析】【分析】根据角平分线求出    ，  再求出 和 ，最后求三角形的周长即可。

27.【解析】【分析】〔1〕先求出 ，再求出 和 ，最后求解即可；
〔2〕先求出 ，再利用三角形的面积公式进行计算求解即可。

28.【解析】【分析】〔1〕先求出 ，再求出AD=DC，最后作答即可；
〔2〕先求出 ，再求出利用ASA证明 ≌   ，最后求解即可。

29.【解析】【分析】〔1〕观察函数图象，利用x轴和y轴的意义即可得出结论；
〔2〕甲行走了60km用了0.75小时，乙行走了60km用了 小时，根据路程与时间的关系即可求解；
〔3〕用待定系数法，根据B点和A点坐标即可求出BD的解析式，根据A点坐标即可求出直线OC的解析式；
〔4〕设甲用时x小时，那么乙为(x+1.75)小时，根据路程相等列方程解答即可.