2020-2021学年北京市门头沟区七年级（上）期末数学试卷

2020-2021学年北京市门头沟区七年级（上）期末数学试卷

一、选择题（本题共16分，每小题2分）下列各题均有四个选项，其中只有一个是符合题意的．

1．（2分）的绝对值是　　

A． B． C． D．3

2．（2分）2020年6月23日，我国北斗卫星导航系统星座部署完成，其中地球同步轨道卫星运行在地球赤道上空约36 000 000米的圆形轨道上．将数字36 000 000用科学记数法表示为　　

A． B． C． D．

3．（2分）某个几何体的展开图如图所示，该几何体是　　

A．长方体 B．圆柱体 C．球体 D．圆锥体

4．（2分）下列计算正确的是　　

A． B． C． D．

5．（2分）永定河，“北京的母亲河”．近年来，我区政府在永定河治理过程中，有时会将弯曲的河道改直，图中、两地间的河道改直后大大缩短了河道的长度．这一做法的主要依据是　　

A．两点确定一条直线 

B．垂线段最短 

C．过一点有且只有一条直线与已知直线垂直 

D．两点之间，线段最短

6．（2分）根据等式的性质，下列变形正确的是　　

A．如果，那么 B．如果，那么 

C．如果，那么 D．如果，那么

7．（2分）有理数在数轴上的对应点的位置如图所示，如果有理数满足，那么的值可以是　　

A．2 B．3 C． D．

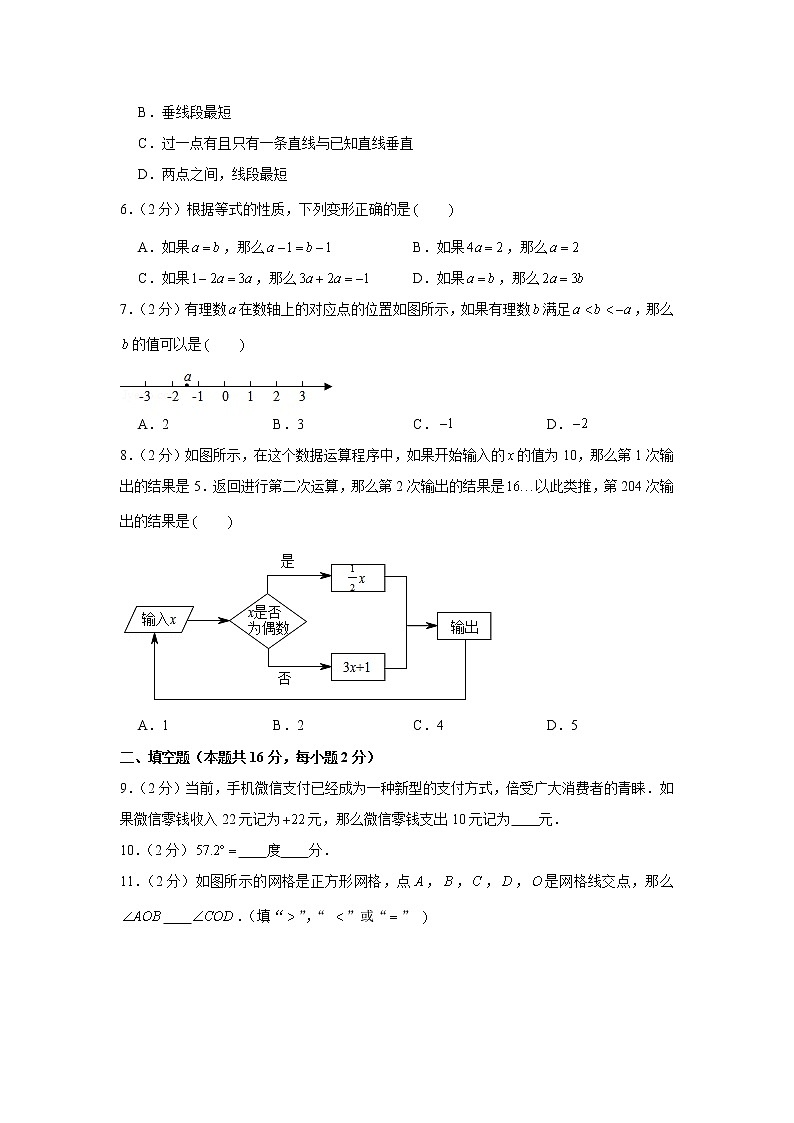
8．（2分）如图所示，在这个数据运算程序中，如果开始输入的的值为10，那么第1次输出的结果是5．返回进行第二次运算，那么第2次输出的结果是以此类推，第204次输出的结果是　　

A．1 B．2 C．4 D．5

二、填空题（本题共16分，每小题2分）

9．（2分）当前，手机微信支付已经成为一种新型的支付方式，倍受广大消费者的青睐．如果微信零钱收入22元记为元，那么微信零钱支出10元记为　　元．

10．（2分）　　度　　分．

11．（2分）如图所示的网格是正方形网格，点，，，，是网格线交点，那么　　．（填“”，“ ”或“”

12．（2分）在下列五个有理数，3.14159，，，0中，最大的整数是　　．

13．（2分）一个单项式满足下列两个条件：①含有两个字母；②次数是3．请写出一个同时满足上述两个条件的单项式　　．

14．（2分）如果是关于的方程的解，那么的值为 　　．

15．（2分）如图，长为的长方形，沿图中虚线裁剪成四个形状大小完全相同的小长方形，那么每个小长方形的周长为　　（用含的代数式表示）．

16．（2分）如图，是北京线地铁的分布示意图，其中桥户营、四道桥、金安桥、苹果园四站在同一条直线上．如果在图中以正东为正方向建立数轴，桥户营站、苹果园站表示的数分别是，2，那么金安桥站表示的数是　　．

三、解答题（本题共68分，17题，17分，18题，9分，19题，5分，20-24题，每题6分，25题，7分）

17．（17分）计算：

（1）；

（2）；

（3）；

（4）．

18．（9分）解方程：

（1）；

（2）．

19．（5分）先化简，再求值：已知，求的值．

20．（6分）如图，已知平面上三点，，，请按要求画图，并回答问题：

（1）画直线，射线；

（2）延长到，使得，连接；

（3）过点画，垂足为；

（4）通过测量可得，点到所在直线的距离约为　　（精确到．

21．（6分）已知，如图，点在线段上，，点是线段的中点，点是线段的中点．求的长．

请将下面的解题过程补充完整：

解：点是线段的中点（已知），

　　（理由：　　

点是线段的中点（已知），

　　．

　　，

　　．

（已知），

　　．

22．（6分）学习了一元一次方程的解法后，老师布置了这样一道计算题，甲、乙两位同学的解答过程分别如下：

老师发现这两位同学的解答过程都有错误．

请你从甲、乙两位同学中，选择一位同学的解答过程，帮助他分析错因，并加以改正．

（1）我选择　　同学的解答过程进行分析（填“甲”或“乙” ；

（2）该同学的解答过程从第　　步开始出现错误（填序号），错误的原因是　　；

（3）请写出正确的解答过程．

23．（6分）为了丰富学生的校园生活，学校组织了“唱响青春”为主题的合唱比赛．初一（2）班准备统一购买演出服装和领结，班干部花费265元，在甲商场购买了3件演出服装和5个领结，已知每件演出服装的标价比每个领结的标价多75元．

（1）求甲商场每件演出服装和每个领结的标价各是多少元？

（2）临近元旦，商场都开始促销活动，同学们发现乙商场也在出售同样的演出服装和领结，并且标价与甲商场相同．但甲商场的促销活动是买一送一（即买一件演出服装送一个领结），乙商场的促销活动是所有商品按标价打九折．如果初一（2）班继续购买30件演出服装和60个领结，去哪家商场购买更合算？

24．（6分）已知，点在直线上，在直线外取一点，画射线，平分．射线在直线上方，且于．

（1）如图1，如果点在直线上方，且，

①依题意补全图1；

②求的度数；

（2）如果点在直线外，且，请直接写出的度数．（用含的代数式表示，且

25．（7分）对数轴上的点进行如下操作：将点沿数轴水平方向，以每秒个单位长度的速度，向右平移秒，得到点．称这样的操作为点的“速移”，点称为点的“速移”点．

（1）当，时，

①如果点表示的数为，那么点的“速移”点表示的数为　　；

②点的“速移”点表示的数为4，那么点表示的数为　　；

③数轴上的点表示的数为1，如果，那么点表示的数为　　；

（2）数轴上，两点间的距离为2，且点在点的左侧，点，通过“2速移”分别向右平移，秒，得到点，，如果，请直接用等式表示，的数量关系．

2020-2021学年北京市门头沟区七年级（上）期末数学试卷

参考答案与试题解析

一、选择题（本题共16分，每小题2分）下列各题均有四个选项，其中只有一个是符合题意的．

1．【解答】解：的绝对值是3，

即．

故选：．

2．【解答】解：36 000 ．

故选：．

3．【解答】解：观察几何体的展开图可知，该几何体是圆柱．

故选：．

4．【解答】解：、，故本选项不合题意；

、，故本选项符合题意；

、，故本选项不合题意；

、与不是同类项，所以不能合并，故本选项不合题意．

故选：．

5．【解答】解：把原来弯曲的河道改直，、两地间的河道长度就发生了变化，

这一做法的主要依据是：两点之间线段最短．

故选：．

6．【解答】解：、在等式的两边都减去1得，原变形正确，故此选项符合题意；

、在等式的两边都除以4得，原变形错误，故此选项不符合题意；

、在等式的两边都加上得，即，原变形错误，故此选项不符合题意；

、在等式的两边都乘以2得，原变形错误，故此选项不符合题意；

故选：．

7．【解答】解：因为，

所以，

因为，

所以只能是．

故选：．

8．【解答】解：根据运算程序可知：

开始输入的的值为10，第1次输出的结果是5．

返回进行第二次运算，第2次输出的结果是16，

第3次输出的结果是8，

第4次输出的结果是4，

第5次输出的结果是2，

第6次输出的结果是1，

第7次输出的结果是4，

，

以此类推，发现规律：

从第4次开始，输出结果是4，2，1三个数一个循环，

，

第204次输出的结果是1．

故选：．

二、填空题（本题共16分，每小题2分）

9．【解答】解：如果微信零钱收入22元记为元，那么微信零钱支出10元记为元．

故答案为：．

10．【解答】解：，

，

故答案为：57，12．

11．【解答】解：如图所示，取格点，作射线，则，

由图可得，，

，

故答案为：．

12．【解答】解：因为，

所以其中最大的整数是．

故答案为：．

13．【解答】解：一个单项式满足下列两个条件：①含有两个字母；②次数是3．

则满足上述条件的单项式为：（答案不唯一）．

故答案为：（答案不唯一）．

14．【解答】解：把代入方程，

得，

解得．

故答案为：．

15．【解答】解：如图，，

解得．

所以．

故答案是：．

16．【解答】解：图中以正东为正方向建立数轴，桥户营站、苹果园站表示的数分别是，2，

每站的单位长度是2，

金安桥站表示的数是0．

故答案为：0．

三、解答题（本题共68分，17题，17分，18题，9分，19题，5分，20-24题，每题6分，25题，7分）

17．【解答】解：（1）原式；

（2）原式；

（3）原式

；

（4）原式

．

18．【解答】解：（1）移项得，

合并得，

系数化为1得；

（2）去括号得，

移项得，

合并得，

系数化为1得．

19．【解答】解：

，

，

原式．

20．【解答】解：（1）如图所示，线，射线即为所求；

（2）如图所示，，即为所求；

（3）如图所示，即为所求；

（4）点到所在直线的距离约为．

故答案为：2.5．

21．【解答】解：点是线段的中点（已知），

（理由：线段中点的定义）

点是线段的中点（已知），

．

，

．

（已知），

．

故答案为：，线段中点的定义，，，，3．

22．【解答】解：（1）我选择乙同学的解答过程进行分析；

（2）该同学的解答过程从第①步开始出现错误（填序号），错误的原因是利用等式的性质漏乘；

（3）方程两边同时乘以4，得：，

去括号，得：，

移项，得：，

合并同类项，得：，

系数化1，得：．

故答案为：（1）乙；（2）①；利用等式的性质漏乘．

23．【解答】解：（1）设每个领结的标价是元，则每件演出服装的标价是元，依题意有

，

解得，

．

故每个领结的标价是5元，则每件演出服装的标价是80元；

（2）甲商场：（元，

乙商场：（元，

，

去乙商场购买更合算．

24．【解答】解：（1）①如图所示：

②，平分，

，

，

，

又点在直线上，

；

（2）分两种情况：

①当点在直线上方时，如图1，

同理可得，，，

；

②当点在直线下方时，如图2，

平分，

，

，

，

，

又点在直线上，

．

综上所述，的度数为或．

25．【解答】解：（1）①点表示的数为，

．

点的“速移”点表示的数为．

故答案为：；

②设点表示的数为，依题意有

，

解得．

故点表示的数为1．

故答案为：1；

③设点表示的数为，则表示的数为，

根据题意得，

解得或．

故答案为：或；

（2）设点表示的数为，点表示的数为，则表示的数为，点表示的数为，

当在右侧时，

，

解得；

当在左侧时，

，

解得．

综上所述，，的数量关系为或．

声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布

日期：2021/11/25 19:53:19；用户：初中数学1；邮箱：keda1618@xyh.com；学号：39816508