浙江省宁波市江北区2021-2022学年上学期九年级第二次月考数学【试卷+答案】（范围：九上全册）

这是一份浙江省宁波市江北区2021-2022学年上学期九年级第二次月考数学【试卷+答案】（范围：九上全册），共17页。试卷主要包含了填空题，解答题等内容，欢迎下载使用。
浙江省宁波市江北区2021-2022学年九年级第二次月考
数学试卷（范围：九上全册）
一、选择题（本题有10个小题，每小题3分，共30分）下面每小题给出的四个选项中，只有一个是正确的.注意可以用多种不同的方法来选取正确答案.
1．（3分）抛物线y＝（x﹣1）2+1的顶点坐标是（　　）
A．（1，1） B．（﹣1，1） C．（1，﹣1） D．（﹣1，﹣1）
2．（3分）下列事件中，属于不可能事件的是（　　）
A．a是实数，则|a|≥0
B．任意一个三角形都有外接圆
C．抛掷一枚骰子，朝上面的点数是6
D．一匹马奔跑的速度是每秒100米
3．（3分）若ba=14，则a+ba=（　　）
A．54 B．45 C．34 D．43
4．（3分）如图，在⊙O中，AB、DC是⊙O的直径，若∠DOA＝70°，则∠C＝（　　）

A．20° B．35° C．55° D．70°
5．（3分）如图，在△ABC中，D、E分别是边AB、BC上的点，且DE∥AC，若S△BDE：S△CDE＝1：3，则S△DOE：S△AOC的值为（　　）

A．13 B．14 C．19 D．116
6．（3分）将抛物线C1：y＝（x﹣2）2向右平移3个单位，再向上平移2个单位得到抛物线C2，则抛物线C2的函数表达式为（　　）
A．y＝（x﹣5）2+2 B．y＝（x﹣5）2﹣2 C．y＝（x+1）2+2 D．y＝（x+1）2﹣2
7．（3分）数轴上有两个点A和B，点B表示实数6，点A表示实数a，⊙B半径为4．若点A在⊙B内，则（　　）
A．a＜2或a＞10 B．2＜a＜10 C．a＞2 D．a＜10
8．（3分）下列不等式成立的是（　　）
A．sin60°＜sin45°＜sin30° B．cos30°＜cos45°＜cos60°
C．tan60°＜tan45°＜tan30° D．sin30°＜cos45°＜tan60°
9．（3分）如图一个扇形纸片的圆心角为90°，半径为6．将这张扇形纸片折叠，使点A与点O恰好重合，折痕为CD，则阴影部分的面积为（　　）

A．93-3π B．6π-93 C．3π-93 D．93-6π
10．（3分）已知二次函数y＝x2﹣bx+c与x轴只有一个交点，且图象经过两点A（1，n），B（m+2，n），则m、n满足的关系为（　　）
A．n=m24 B．n=m22 C．n=(m+1)24 D．n=(m+1)22
二、填空题：本大题有6个小题，每小题4分，共24分.
11．已知a＝3，b＝27，则a，b的比例中项为　 　．
12．如图，若△ABC与△DEF都是正方形网格中的格点三角形（顶点在格点上），则△DEF与△ABC的周长比为　 　．

13．把只有颜色不同的1个白球和2个红球装入一个不透明的口袋里搅匀，从中随机地摸出1个球后放回搅匀，再次随机地摸出1个球，两次都摸到红球的概率为　 　．
14．某工厂1月份的产值是200万元，平均每月产值的增长率为x（x＞0），则该工厂第一季度的产值y关于x的函数解析式为　 　．
15．如图，在Rt△ABC中，∠C＝90°，BC＝3，AC＝4，△A′B′C≌△ABC．点B′正好落在AB上，A′B′与AC相交于点D，那么＝　 　．

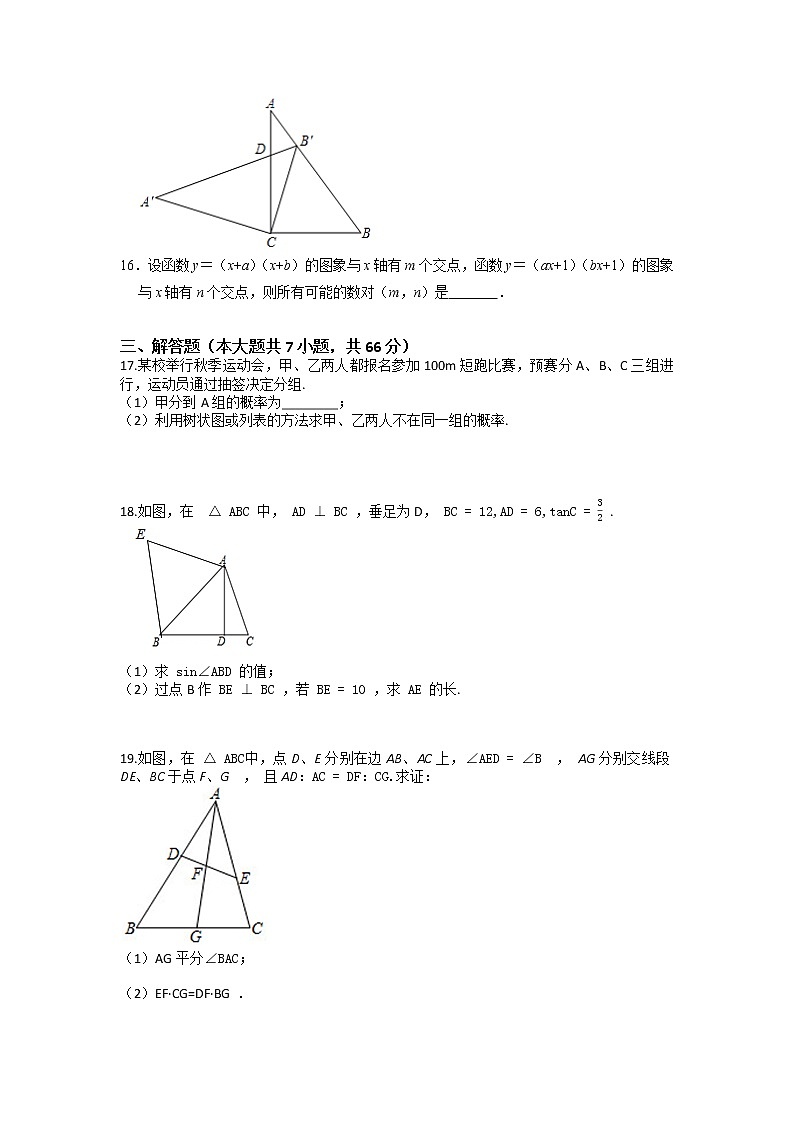
16．设函数y＝（x+a）（x+b）的图象与x轴有m个交点，函数y＝（ax+1）（bx+1）的图象与x轴有n个交点，则所有可能的数对（m，n）是　 　．

三、解答题（本大题共7小题，共66分）
17.某校举行秋季运动会，甲、乙两人都报名参加100m短跑比赛，预赛分A、B、C三组进行，运动员通过抽签决定分组.
（1）甲分到A组的概率为________；
（2）利用树状图或列表的方法求甲、乙两人不在同一组的概率.




18.如图，在 △ABC 中， AD⊥BC ，垂足为D， BC=12,AD=6,tanC=32 .

（1）求 sin∠ABD 的值；
（2）过点B作 BE⊥BC ，若 BE=10 ，求 AE 的长.



19.如图，在△ABC中，点D、E分别在边AB、AC上，∠AED=∠B ， AG分别交线段DE、BC于点F、G ， 且AD：AC=DF：CG.求证：

（1）AG平分∠BAC；

（2）EF·CG=DF·BG ．

20.如图1，AC⊥CH于点C ， 点B是射线CH上一动点，将△ABC绕点A逆时针旋转60°得到△ADE（点D对应点C）．

（1）延长ED交CH于点F ， 求证：FA平分∠CFE；
（2）如图2，当∠CAB＞60°时，点M为AB的中点，连接DM ， 请判断DM与DA、DE的数量关系，并证明．








21.在“母亲节”期间，某校部分团员参加社会公益活动，准备购进一批许愿瓶进行
销售，并将所得利润捐给慈善机构．根据市场调查，这种许愿瓶一段时间内的销售量y(个)于销售单价x(元/个)之间的对应关系如图所示．

（1）试判断y与x之间的函数关系，并求出函数关系式；
（2）若许愿瓶的进价为6元/个，按照上述市场调查销售规律，求利润w(元)与销售单价x(元/个)之间的
函数关系式；
（3）若许愿瓶的进货成本不超过900元，要想获得最大利润，试求此时这种许愿瓶的销售单价，并求出
最大利润












22.如图，抛物线 y=ax2-32x+c(a≠0) 与x轴交于点A，B，与y轴交于点 C(0,-2) ， tan∠ABC=12 .直线 x=1 交 BC 于点D，点P是直线 BC 下方抛物线上一动点，连接PD.
     
（1）求此抛物线的解析式；
（2）如图1，连接 PC ，求 △PCD 面积的最大值及此时点P的坐标；
（3）如图2，连接 AC ，过点P作 PE⊥BC 于点E，是否存在点P使以P，D，E三点为顶点的三角形与 △ABC 相似，若存在，直接写出点P的坐标；若不存在，请说明理由.










23.如图，△ABC内接于⊙O，AD平分∠BAC交BC边于点E，交⊙O于点D，过点A作AF⊥BC
于点F，设⊙O的半径为R，AF＝h．

（1）过点D作直线MN∥BC，求证：MN是⊙O的切线；
（2）求证：AB•AC＝2R•h；
（3）设∠BAC＝2α，求 AB+ACAD 的值（用含α的代数式表示）．









参考答案
一、选择题（本题有10个小题，每小题3分，共30分）下面每小题给出的四个选项中，只有一个是正确的.注意可以用多种不同的方法来选取正确答案.
1．【解答】解：因为y＝（x﹣1）2+1是抛物线解析式的顶点式，
根据顶点式的坐标特点可知，顶点坐标是（1，1）．
故选：A．
2． 【解答】解：A、a是实数，则|a|≥0，是必然事件；
B、任意一个三角形都有外接圆，是随机事件；
C、抛掷一枚骰子，朝上面的点数是6，是随机事件；
D、一匹马奔跑的速度是每秒100米，是不可能事件；
故选：D．
3．【解答】解：∵ba=14，
∴a＝4b
∴a+ba=4b+b4b=54．
故选：A．
4． 【解答】解：∵OA＝OC，
∴∠A＝∠C，
∵∠AOD＝∠A+∠C＝70°，
∴∠C＝35°，
故选：B．
5．【解答】 解：∵S△BDE：S△CDE＝1：3，
∴BE：EC＝1：3；
∴BE：BC＝1：4；
∵DE∥AC，
∴△DOE∽△AOC，
∴DEAC=BEBC=14，
∴S△DOES△AOC=(DEAC)2=116，
故选：D．

6．【解答】解：将抛物线y＝（x﹣2）2向右平移3个单位，再向上平移2个单位后所得直线解析式为：y＝（x﹣2﹣3）2+2，即y＝（x﹣5）2+2．
故选：A．
7．【解答】解：∵点B表示实数6，⊙B半径为4．
∴数轴与⊙B的交点表示的数为2或10，
∵点A表示实数a，点A在⊙B内，
∴2＜a＜10，
故选：B．
8． 【解答】解：A、∵32＞22＞12，
∴sin60°＞sin45°＞sin30°，故选项不成立；
B、∵32＞22＞12，
∴cos30°＞cos45°＞cos60°，故选项不成立；
C、∵3＞1＞33，
∴tan60°＞tan45°＞tan30°，故选项不成立；
D、∵12＜22＜3，
∴sin30°＜cos45°＜tan60°，故选项成立．
故选：D．
9．
【解答】解：连接OD，如图，
∵扇形纸片折叠，使点A与点O恰好重合，折痕为CD，
∴AC＝OC，
∴OD＝2OC＝6，
∴CD=62-32=33，
∴∠CDO＝30°，∠COD＝60°，
∴由弧AD、线段AC和CD所围成的图形的面积＝S扇形AOD﹣S△COD=60π×62360-12×3×33=6π-932，
∴阴影部分的面积为90π×62360-2×（6π-932）＝93-3π，
故选：A．
10．【解答】解：∵点A、B的纵坐标相同，
∴函数的对称轴为x=12（1+m+2）=m+32=b2×1，
解得b＝m+3，
∵二次函数y＝x2﹣bx+c与x轴只有一个交点，
则△＝b2﹣4c＝（m+3）2﹣4c＝0，解得c=14（m+3）2，
当x＝1时，y＝n＝1﹣b+c＝1﹣（m+3）+14（m+3）2=(m+1)24，
故选：C．
二．填空题（共6小题）
11． 【分析】根据比例中项的定义直接列式求值，问题即可解决．
【解答】解：设a、b的比例中项为x，
∵a＝3，b＝27，
∴，
即x2＝81，
∴x＝±9，
∴a，b的比例中项为±9，
故答案为：±9．
12．【分析】如图，设正方形网格的边长为1，根据勾股定理求出△EFD、△ABC的边长，运用三边对应成比例，则两个三角形相似这一判定定理证明△EDF∽△BAC，即可解决问题．
【解答】解：设正方形网格的边长为1，由勾股定理得：
DE2＝22+22，EF2＝22+42，
∴DE＝2，EF＝2；
同理可求：AC＝，BC＝，
∵DF＝2，AB＝2，
∴＝＝＝，
∴△EDF∽△BAC，
∴△DEF与△ABC的周长比为：：1．
故答案为：：1．
13． 【分析】画树状图，共有9种等可能情况，两次都摸到红球的有4种情况，再由概率公式求解即可．
【解答】解：画树状图如图所示：

共有9种等可能情况，两次都摸到红球的有4种情况，
∴两次都摸到红球的概率为，
故答案为：．
14． 【分析】首先分别表示出二月、三月的产值，然后再列出函数解析式即可．
【解答】解：由题意得：y＝200+200x+200（1+x）2＝200+200x+200+400x+200x2＝200x2+600x+400，
故答案为：y＝200x2+600x+400．
15．【分析】作辅助线；首先求出BM的长度，进而求出AC、BB′的长度；证明△A′DC∽△ADB′，得，即可解决问题．
【解答】解：如图，过点C作CM⊥AB于点M，
∵∠C＝90°，BC＝3，AC＝4，
∴AB＝5，
∴；设BC＝3λ，则AB＝5λ，
由勾股定理得AC＝4λ，
由射影定理得：BC2＝BM•AB，
∴BM＝λ．
由△A′B′C≌△ABC得：
CB＝CB′，A′C＝AC＝4λ，∠A′＝∠A；而CM⊥BB′，
∴B′M＝BM，AB′＝5λ﹣λ＝λ，
∵∠A′＝∠A，∠A′DC＝∠ADB′，
∴△A′DC∽△ADB′，
∴，
故答案为：．

16． 【分析】分m＝1和m＝2两种情况，利用函数和x轴交点情况，分别求解即可．
【解答】解：（1）当m＝1时，则a＝b，
当ab≠0时，则y＝（ax+1）（bx+1）＝abx2+（a+b）x+1＝a2x2+2ax+1，则△＝4a2﹣4a2＝0，故n＝1，
当ab＝0时，同理函数的表达式为y＝1，则n＝0；
（2）当m＝2时，则a≠b，
当ab≠0时，则y＝（ax+1）（bx+1）＝abx2+（a+b）x+1，则△＝（a+b）2﹣4ab＝（a﹣b）2＞0，故n＝2，
当ab＝0时，同理函数的表达式为y＝（a+b）x+1，则n＝1；
故答案为：（1，1）、（1，0）、（2，2）、（2
三、解答题（本大题共7小题，共66分）
17.【答案】 （1）13
（2）解：甲乙两人抽签分组所有可能出现的结果有：（A，A）、（A，B）、（A，C）、（B，A）、（B，B）、（B，C）、（C，A）、（C，B）、（C，C）共有9种，它们出现的可能性相同.所有的结果中，甲乙分到同一组的结果有3种，甲乙不在同一组的结果6种，所以P(甲乙不在同一组)＝ 69=23 .
【考点】列表法与树状图法，概率公式
【解析】【解答】解：（1）甲分到A组一种情况，总的有三种，则P（A）= 13 ，
【分析】（1）共有A、B、C三种等可能性，而甲分到A组一种情况，利用概率公式计算即可；
（2）列举出共有9种等可能结果，其中甲乙分到同一组的结果有3种，利用概率公式计算即可.
18.【答案】 （1）解：在Rt△ADC中
∵ AD=6,tanC=32
∴CD=4
∴BD=12－4=8
在Rt△ABD中，根据勾股定理可得
AB=BD2+AD2=10  
∴ sin∠ABD=ADAB=610=35

（2）解：作AF⊥BE于点F

∵ BE⊥BC ， AD⊥BC
∴四边形ADBF是矩形
∴AF=BD=8，AD=BF=6
∴EF=10－6=4
在Rt△AEF中，根据勾股定理可得
AB=AF2+EF2=45
【考点】矩形的判定与性质，解直角三角形
【解析】【分析】（1） 在Rt△ADC中， 根据tanC=AD CD 可求得CD的值，再根据线段的构成BD=BC-CD可求得BD的值；在Rt△ADC中，由勾股定理可求得AB的值，再根据sin∠ABD=ADAB可求解；
（2） 作AF⊥BE于点F， 由矩形的判定易得四边形ADBF是矩形 ，根据矩形的性质可得AF=BD，AD=BF， 在Rt△AEF中，根据勾股定理可求得AB的值.
19.【答案】 （1）证明：如图所示：

∵∠DAE+∠AED+∠ADE=180° ，
∠BAC+∠B+∠C=180° ， ∠AED=∠B ， ∴∠ADE=∠C ，
在 △ADF 和 △ACG 中，
{AD:AC=DF:CG∠ADE=∠C  
∴△ADF ∽ △ACG ， ∴∠DAF=∠CAG ，
∴AG 平分 ∠BAC

（2）证明：在 △AEF 和 △ABG 中，
{∠AED=∠B∠EAF=∠BAG ，
∴△AEF ∽ △ABG ，
∴EFBG=AFAG ，
在 △ADF 和 △AGC 中，
{∠DAF=∠CAG∠ADF=∠C ，
∴△ADF ∽ △AGC ，
∴DFCG=AFAG ，
∴EFBG=DFCG ，
∴EF⋅CG=DF⋅BG ．
【考点】相似三角形的判定与性质
【解析】【分析】（1）根据相似三角形的判定可得三角形相似，再得到对应角相等，即可证明AG平分 ∠BAC ；
（2）根据相似三角形的判定与性质证明求解即可。
20.【答案】 （1）如图1中，

∵△ADE由△ABC旋转得到，
∴AC＝AD，∠ACF＝∠ADE＝∠ADF＝90°，AF=AF
∴ △ACF≌△ADF (HL)，
∴∠AFC=∠AFD ， FA平分∠CFE；

（2）结论： 2DM+3AD=DE ，
理由如下：如图2中，延长AD交BC于F，连接CD，

∵AC＝AD，∠CAD＝60°，
∴△ACD为等边三角形，
∴AD＝CD＝AC，
∵∠ACF＝90°，∠CAF＝60°，
∴∠AFC＝30°，
∴AD＝AC＝ 12 AF，
∴AD＝DF，
∴D为AF的中点，
又∵M为AB的中点，
∴DM＝ 12 FB，即FB=2DM
在Rt△AFC中，FC＝ 3 AC= 3 AD，
∵   DE=CB=FB+FC ，
∴FB+FC=2DM+3AD
∴ 2DM+3AD=DE ．
【考点】直角三角形全等的判定（HL），旋转的性质，三角形的综合
【解析】【分析】（1）根据直角三角形全等判定，得到对应角相等，根据角分线定义证明．（2）延长AD交BC于F ， 连接CD；利用旋转的到特殊值三角形，运用三角形的中位线定理，将DE解转化到CB决问题即可．
21.【答案】 （1）解：y是x的一次函数，设y=kx+b，
∵图象过点（10，300），（12，240），
∴ {10k+b=30012k+b=240 ，解得 {k=-30b=600 ．∴y=－30x＋600．
当x=14时，y=180；当x=16时，y=120，
∴点（14，180），（16，120）均在函数y=－30x+600图象上．
∴y与x之间的函数关系式为y=－30x+600．

（2）解：∵w=（x－6）（－30x＋600）=－30x2＋780x－3600，
∴w与x之间的函数关系式为w=－30x2＋780x－3600．

（3）解：由题意得：6（－30x+600）≤900，解得x≥15．
w=－30x2＋780x－3600图象对称轴为： x=-7802×(-30)=13 ．
∵a=－30＜0，∴抛物线开口向下，当x≥15时，w随x增大而减小．
∴当x=15时，w最大=1350．
∴以15元/个的价格销售这批许愿瓶可获得最大利润1350元．
【考点】待定系数法求一次函数解析式，二次函数的实际应用-销售问题
【解析】【分析】（1）观察可得该函数图象是一次函数，设出一次函数解析式，把其中两点代入即可求得该函数解析式，进而把其余两点的横坐标代入看纵坐标是否与点的纵坐标相同．（2）销售利润=每个许愿瓶的利润×销售量．（3）根据进货成本可得自变量的取值，结合二次函数的关系式即可求得相应的最大利润．
22.【答案】 （1）解： ∵C(0,-2) ，
∴OC=2 ，
∵ 在 Rt△BOC 中， tan∠ABC=OCOB=2OB=12 ，
∴OB=4 ，即 B(4,0) ，
将点 B(4,0),C(0,-2) 代入抛物线的解析式得： {16a-6+c=0c=-2 ，
解得 {a=12c=-2 ，
则此抛物线的解析式为 y=12x2-32x-2 ；

（2）解：设直线BC的函数解析式为 y=kx+b ，
将点 B(4,0),C(0,-2) 代入得： {4k+b=0b=-2 ，解得 {k=12b=-2 ，
则直线BC的函数解析式为 y=12x-2 ，
当 x=1 时， y=12×1-2=-32 ，即 D(1,-32) ，
则 CD=(1-0)2+(-32+2)2=52 ，
要使 △PCD 的面积最大，则需要点P到CD的距离最大，
设与直线BC平行的直线 l' 的函数解析式为 y=12x+d ，则 F(0,d),CF=-2-d ，
如图，过点C作 CE⊥l' 于点E，则CE为直线BC与直线 l' 间的距离，

在 Rt△BOC 中， OB=4,BC=OB2+OC2=25 ，则 sin∠OCB=OBBC=255 ，
∵BC//l' ，
∴∠CFE=∠OCB ，
∴sin∠CFE=sin∠OCB=255 ，
在 Rt△CEF 中， sin∠CFE=CECF=CE-2-d=255 ，
解得 CE=255(-2-d) ，
∴d 越小，CE越大，当直线 l' 要与抛物线 y=12x2-32x-2 有交点，
即当直线 l' 与 y=12x2-32x-2 有且只有一个交点时， d 最小，此时的交点即为点P，
联立 {y=12x2-32x-2y=12x+d ，
整理得： 12x2-2x-2-d=0 ，
则其根的判别式 Δ=4-4×12(-2-d)=0 ，
解得 d=-4 ，
则此时 CE=255×(-2+4)=455 ，
△PCD 面积的最大值为 12×52×455=1 ，
将 d=-4 代入 12x2-2x-2-d=0 得： x1=x2=2 ，
当 x=2 时， y=12×22-32×2-2=-3 ，
∴△PCD 面积取得最大值时，点P的坐标为 (2,-3) ；

（3）解：对于 y=12x2-32x-2 ，
当 y=0 时， 12x2-32x-2=0 ，解得 x=-1,x=4 ，
∴A(-1,0) ，
∵B(4,0),C(0,-2) ，
∴AB=4+1=5,AC=12+22=5,BC=22+42=25 ，
∴AC2+BC2=AB2 ，
∴△ABC 是直角三角形，且 ∠ACB=90° ，
设点P的坐标为 (m,12m2-32m-2) ，
∵PE⊥BC ，直线BC的函数解析式为 y=12x-2 ，
∴ 设直线PE的函数解析式为 y=-2x+n ，
将 (m,12m2-32m-2) 代入得： -2m+n=12m2-32m-2 ，
解得 n=12m2+12m-2 ，
则直线PE的函数解析式为 y=-2x+12m2+12m-2 ，
联立 {y=-2x+12m2+12m-2y=12x-2 ，解得 {x=15m2+15my=110m2+110m-2 ，
即 E(15m2+15m,110m2+110m-2) ，
∴PE2=(15m2-45m)2+(25m2+85m)2 ，
DE2=(15m2+15m-1)2+(110m2+110m-12)2 ，
由题意，分以下两种情况：
①当 Rt△PDE∼Rt△ABC 时，
则 PEDE=ACBC=525=12 ，即 DE2=4PE2 ，
解得 m=3+132 或 m=17-2296 ，
则此时 P(3+132,132) 或 P(17-2296,17-1022918) ；
②当 Rt△DPE∼Rt△ABC 时，
则 PEDE=BCAC=255=2 ，即 PE2=4DE2 ，
解得 m=52 ，
则此时 P(52,-218) ；
综上，存在这样的点P，此时点P的坐标为 P(3+132,132) 或 P(17-2296,17-1022918) 或 P(52,-218) .
【考点】二次函数的实际应用-几何问题
【解析】【分析】（1）在Rt△BOC中，根据tan∠ABC=OCOB可求得OB的值，将点B、C的坐标代入抛物线的解析式可得关于a、c的方程组，解之可求解；
（2）由题意可用待定系数法求得直线BC的解析式，由题意把x=1代入直线BC的解析式可求得点D的坐标；由勾股定理可求得CD的值； 要使△PCD的面积最大，则需要点P到CD的距离最大；设与直线BC平行的直线 l' 的函数解析式为y=12x+d，则F（0，d）,于是CF可用含d的代数式表示出来，如图，过点C作 CE⊥l' 于点E，则CE为直线BC与直线 l' 间的距离， 解直角三角形BOC和直角三角形CEF可将CE用含d的代数式表示出来，由一次函数的性质可知：d越小，CE越大，当直线l与抛物线有交点即当直线l与抛物线有且只有一个交点时，d最小，此时的交点即为点P，把直线l和抛物线的解析式联立解方程组整理可得关于x 的一元二次方程，根据两个图像只有一个交点可得这个一元二次方程的b2-4ac=0，则可得关于d的方程，解之可求得d的值，则结论可求解；
（3）由题意先求得抛物线与x轴的交点A的坐标，根据勾股定理的逆定理可得△ABC是直角三角形，设点P的横坐标为m，根据点P在抛物线上，点P的纵坐标可用含m的代数式表示出来，根据PE⊥BC可知直线PE的k值与直线BC的k值互为负倒数，于是直线PE可用含n的代数式表示，把点P的坐标代入直线PE的解析式可得关于m、n的方程，则n可用含m的代数式表示，于是直线PE的解析式可用含m的代数式表示，把直线PE和直线BC的解析式联立解方程组可得点E的坐标，用勾股定理可将PE2和DE2用含m的代数式表示，由题意分两种情况讨论求解：①当Rt△PDE∽Rt△ABC时，可得比例式PEDE=ACBC求解；
②当Rt△DPE∽Rt△ABC时，可得比例式PEDE=BCAC求解.
23.【答案】 （1）解：证明：如图1，连接OD，

∵AD平分∠BAC，∴∠BAD＝∠CAD，∴ BD ＝ CD ，
又∵OD是半径，∴OD⊥BC，
∵MN∥BC，∴OD⊥MN，∴MN是⊙O的切线；

（2）证明：如图2，连接AO并延长交⊙O于H，

∵AH是直径，∴∠ABH＝90°＝∠AFC，
又∵∠AHB＝∠ACF，
∴△ACF∽△AHB，
∴ ACAH=AFAB ，
∴AB•AC＝AF•AH＝2R•h；

（3）解：如图3，过点D作DQ⊥AB于Q，DP⊥AC，交AC延长线于P，连接CD，

∵∠BAC＝2α，AD平分∠BAC，
∴∠BAD＝∠CAD＝α，∴ BD ＝ CD ，∴BD＝CD，
∵∠BAD＝∠CAD，DQ⊥AB，DP⊥AC，∴DQ＝DP，
∴Rt△DQB≌Rt△DPC（HL），∴BQ＝CP，
∵DQ＝DP，AD＝AD，
∴Rt△DQA≌Rt△DPA（HL），∴AQ＝AP，
∴AB+AC＝AQ+BQ+AC＝2AQ，
∵cos∠BAD＝ AQAD ，∴AD＝ AQcosα ，∴ AB+ACAD ＝ 2AQAQcosα ＝2cosα．
【考点】全等三角形的性质，垂径定理，切线的判定，相似三角形的判定与性质，锐角三角函数的定义
【解析】【分析】（1）连接OD，由角平分线的性质可得∠BAD＝∠CAD，可得 BD ＝ CD ，由垂径定理可得OD⊥BC，可证OD⊥MN，可得结论；（2）连接AO并延长交⊙O于H，通过证明△ACF∽△AHB，可得 ACAH=AFAB ，可得结论；（3）由“HL”可证Rt△DQB≌Rt△DPC，Rt△DQA≌Rt△DPA，可得BQ＝CP，AQ
＝AP，可得AB+AC＝2AQ，由锐角三角函数可得AD＝ AQcosα ，即可求解．