2018-2019学年河北省石家庄市桥西区八年级（下）期末数学试卷

这是一份2018-2019学年河北省石家庄市桥西区八年级（下）期末数学试卷，共27页。试卷主要包含了精心选择，准确填空，挑战技能，能力展示，挑战自我等内容，欢迎下载使用。

1．（2分）下列函数中，是正比例函数的是（ ）
A．B．y＝2x2C．y＝x+2D．y＝﹣2x
2．（2分）一次函数y＝2﹣x与x轴的交点为（ ）
A．（1，1）B．（0，2）C．（2，0）D．（3，0）
3．（2分）如图，小手盖住的点的坐标可能是（ ）
A．（4，﹣1）B．（﹣1，﹣4）C．（2，3）D．（﹣2，2）
4．（2分）已知▱ABCD的周长为24，△ABD的周长为19，则对角线BD的长是（ ）
A．4B．5C．6D．7
5．（2分）下列调查中，你认为最适宜用普查的是（ ）
A．调查一批显像管的使用寿命
B．调查全班学生的视力情况
C．调查某罐头厂生产的一批罐头的质量
D．调查全市中学生每天体育锻炼的时间
6．（2分）一个多边形的每一个外角都是45°，则这个多边形的边数为（ ）
A．6B．7C．8D．9
7．（2分）已知点A与点B关于x轴对称，若点A的坐标为（﹣1，3），点B的坐标为（﹣1，b），则b的值等于（ ）
A．﹣3B．﹣1C．1D．3
8．（2分）在函数y＝中，自变量x的取值范围是（ ）
A．x≠3B．x≥0C．x≥3D．x＞3
9．（2分）某校有500名学生参加体育测试，其成绩在25﹣30分之间的有300人，则在25﹣30分之间的频率是（ ）
A．0.6B．0.5C．0.3D．0.1
10．（2分）已知正比例函数y＝kx（k≠0）的函数值随x的增大而增大，则一次函数y＝x+2k的图象大致是（ ）
A．B．
C．D．
11．（2分）关于▱ABCD的叙述，正确的是（ ）
A．若AC＝BD，则▱ABCD是菱形
B．若AB＝AD，则▱ABCD是矩形
C．若AB⊥BC，则▱ABCD是正方形
D．若AC⊥BD，则▱ABCD是菱形
12．（2分）对于函数y＝﹣x+3，下列结论正确的是（ ）
A．当x＞4时，y＜0
B．它的图象经过第一、二、三象限
C．它的图象必经过点（﹣1，3）
D．y的值随x值的增大而增大
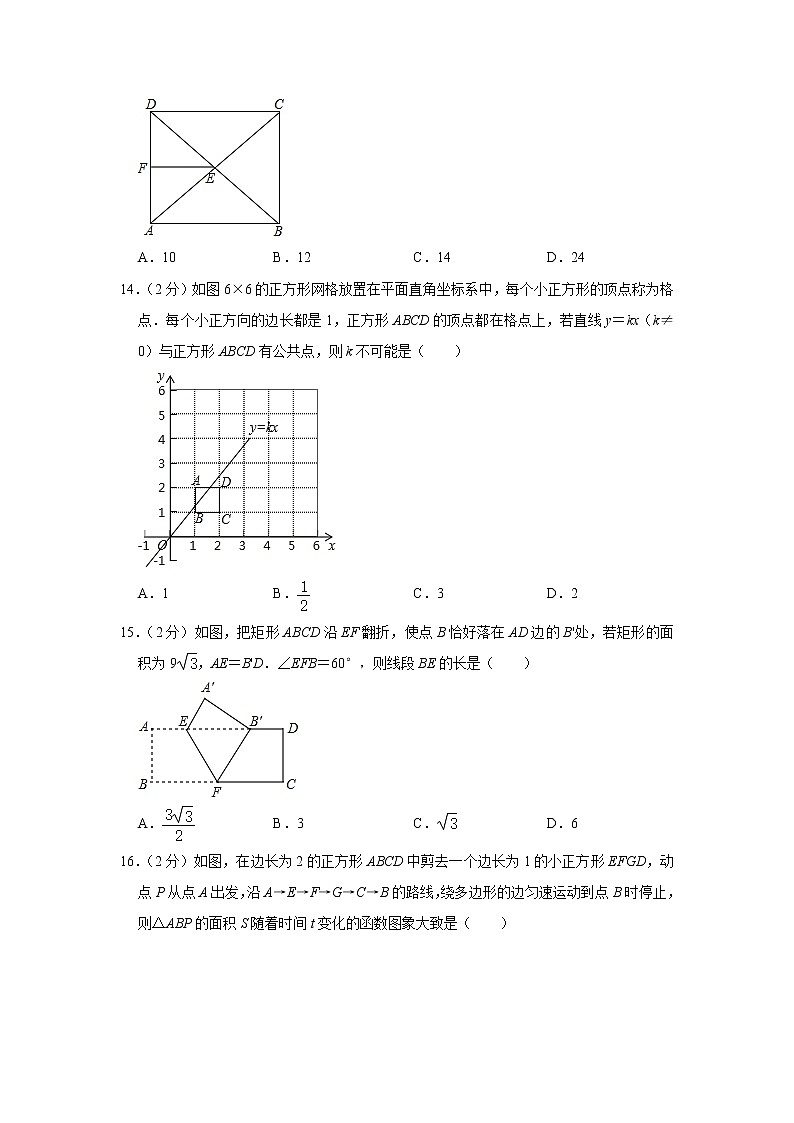
13．（2分）如图所示，在矩形ABCD中，点E是对角线AC，BD的交点，点F是边AD的中点且AB＝8，BC＝6，则△DEF的周长是（ ）
A．10B．12C．14D．24
14．（2分）如图6×6的正方形网格放置在平面直角坐标系中，每个小正方形的顶点称为格点．每个小正方向的边长都是1，正方形ABCD的顶点都在格点上，若直线y＝kx（k≠0）与正方形ABCD有公共点，则k不可能是（ ）
A．1B．C．3D．2
15．（2分）如图，把矩形ABCD沿EF翻折，使点B恰好落在AD边的B'处，若矩形的面积为9，AE＝B'D．∠EFB＝60°，则线段BE的长是（ ）
A．B．3C．D．6
16．（2分）如图，在边长为2的正方形ABCD中剪去一个边长为1的小正方形EFGD，动点P从点A出发，沿A→E→F→G→C→B的路线，绕多边形的边匀速运动到点B时停止，则△ABP的面积S随着时间t变化的函数图象大致是（ ）
A．B．
C．D．
二、准确填空（本大题共3个小题，17、18每小题3分，19题每空2分，共10分，）
17．（3分）点P（2，4）到y轴的距离是
18．（3分）已知直线y＝ax+b与y＝x交于点P（﹣4，﹣2），则关于x，y的二元一次方程组的解是 ．
19．（4分）如图，将矩形ABCD在直线上按顺时针方向无滑动翻滚，可依次得到矩形A1B1C1D1，矩形A2B2C1D1矩形A3B2C2D2，…，若AB＝2，BC＝4，那么AA3的长为 ，AA15的长为 ．
三、挑战技能（本大题共4个小题，20、21题每题6分，22、23题每题8分，共28分）
20．（6分）如图表示的是热带风暴从发生到结束的全过程．请结合图象回答下列问题：
（1）热带风暴从开始发生到结束共经历了 个小时；
（2）从图象上看，风速在 （小时）时间段内增大的最快，最大风速是 千米/小时；
（3）风速从开始减小到最终停止，平均每小时减小多少千米？
21．（6分）如图，已知网格线是由边长为1的小正方形组成，△A′B′C′是由△ABC平移得到的，建立适当的平面直角坐标系后，C点坐标为（1，2）
（1）请在图中画出这个平面直角坐标系；
（2）根据（1）中建立的平面直角坐标系，点A′，B′，C′的坐标分别是A′ B′ C′ ；
（3）若△ABC内点P的坐标为（a，b），写出平移后点P的对应点P′的坐标．
22．（8分）某中学计划根据学生的兴趣爱好组建课外兴趣小组，并随机抽取了部分同学的兴趣爱好进行调查，将收集的数据整理并绘制成下列两幅统计图，请根据图中的信息，完成下列问题：
（1）学校这次调查共抽取了 名学生；
（2）求m的值并补全条形统计图；
（3）在扇形统计图，“围棋”所在扇形的圆心角度数为 ；
（4）设该校共有学生1000名，请你估计该校有多少名学生喜欢足球．
23．（8分）学校计划购买一批标有单价为3000元的某型号电脑，需要数量在10至20台之间，以下是甲、乙两个商家的优惠政策，学校购买哪家的电脑更合算呢？
优惠政策：
甲店：每台八折．
乙店：先赠一台，其余每台九折．
四、能力展示（本大题共2个小题，24题9分、25题10分，共19分）
24．（9分）如图1，△ABC中，AB＝AC，点D（不与点B重合）在BC上，点E是AB的中点，过点A作AF∥BC交DE延长线于点F
（1）求证：△AEF≌△BED；
（2）小明在完成（1）的证明后继续探索，连接AD，BF，如图2所示，并提出猜想，你觉得小明的猜想正确吗？请说明理由．
小明：如果AD平分∠BAC，那么四边形AFBD是矩形．
25．（10分）甲、乙两车间同时开始加工一批零件，从开始加工到加工完这批零件，甲车间工作了10个小时，乙车间在中间停工一段时间维修设备，然后按停工前的共作效率继续加工，直到与甲车间同时完成这批零件的加任务为止．设甲、乙两车间各自加工零件的数量为y（个），甲车间加工的时间为x（时），y与x之间的函数图象如图所示．
（1）甲车间每小时加工零件的个数为 个；这批零件的总个数为 个；
（2）求乙车间维护设备后，乙车间加工零件的数量y与x之间的函数关系式；
（3）在加工这批零件的过程中，当甲、乙两车间共同加工完930个零件时，求甲车间的时间．
五、挑战自我（本大题11分）
26．（11分）如图1所示，把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起，使三角板的直角顶点和正方形的顶点C重合，点E，F分别在正方形的边CB，CD上，连接AE、AF．
（1）求证：AE＝AF；
（2）取AF的中点M，EF的中点N，连接MD，MN．则MD，MN的数量关系是 ，MD、MN的位置关系是
（3）将图2中的直角三角板ECF，绕点C旋转180°，图3所示，其他条件不变，则（2）中的两个结论还成立吗？若成立，请加以证明；若不成立，请说明理由．
2018-2019学年河北省石家庄市桥西区八年级（下）期末数学试卷
参考答案与试题解析
一、精心选择（本大题共16个小题，每小题2分，共32分，在每个小题给出的四个选项中，只有一项是正确的，请把正确选项的代码填在题后的括号内）
1．（2分）下列函数中，是正比例函数的是（ ）
A．B．y＝2x2C．y＝x+2D．y＝﹣2x
【分析】一般地，形如y＝kx（k是常数，k≠0）的函数叫做正比例函数，其中k叫做比例系数．
【解答】解：A、分母中含有自变量x，不是正比例函数，故A错误；
B、y＝2x2是二次函数，故B错误；
C、y＝x+2是一次函数，故C错误；
D、y＝﹣2x是正比例函数，故D正确．
故选：D．
【点评】本题主要考查的是一次函数的定义，熟练掌握一次函数的定义是解题的关键．
2．（2分）一次函数y＝2﹣x与x轴的交点为（ ）
A．（1，1）B．（0，2）C．（2，0）D．（3，0）
【分析】根据一次函数图象与x轴交点的纵坐标等于零解答．
【解答】解：令y＝0，则2﹣x＝0，解得 x＝2，
所以一次函数y＝2﹣x与x轴的交点坐标是 （2，0），
故选：C．
【点评】本题考查了一次函数图象上点的坐标特征．一次函数y＝kx+b，（k≠0，且k，b为常数）的图象是一条直线．它与x轴的交点坐标是（﹣，0）；与y轴的交点坐标是（0，b）．
3．（2分）如图，小手盖住的点的坐标可能是（ ）
A．（4，﹣1）B．（﹣1，﹣4）C．（2，3）D．（﹣2，2）
【分析】先判断出小手盖住的点在第二象限，再根据各象限内点的坐标特征解答．
【解答】解：由图可知，小手盖住的点在第二象限，
（4，﹣1），（﹣1，﹣4），（2，3），（﹣2，2）中只有（﹣2，2）在第二象限．
故选：D．
【点评】本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣）．
4．（2分）已知▱ABCD的周长为24，△ABD的周长为19，则对角线BD的长是（ ）
A．4B．5C．6D．7
【分析】利用平行四边形的性质可知AD＝BC，AB＝CD，可求得AB+AD，再结合△ABD的周长可求得BD．
【解答】解：∵四边形ABCD为平行四边形，
∴AB＝CD，AD＝BC，
∴2（AB+AD）＝24，
∴AB+AD＝12，
又∵△ABD的周长为19，
∴AB+AD+BD＝19，
∴12+BD＝19，
∴BD＝7，
故选：D．
【点评】本题主要考查平行四边形的性质，掌握平行四边形的对边相等是解题的关键．
5．（2分）下列调查中，你认为最适宜用普查的是（ ）
A．调查一批显像管的使用寿命
B．调查全班学生的视力情况
C．调查某罐头厂生产的一批罐头的质量
D．调查全市中学生每天体育锻炼的时间
【分析】由普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果比较近似．
【解答】解：A、调查一批显像管的使用寿命具有破坏性，适合抽样调查，故A不符合题意；
B、调查全班学生的视力情况，适合普查，故B符合题意；
C、调查某罐头厂生产的一批罐头的质量，适合抽样调查，故C不符合题意；
D、调查全市中学生每天体育锻炼的时间调查范围广，适合抽样调查，故D不符合题意；
故选：B．
【点评】本题考查了抽样调查和全面调查的区别，选择普查还是抽样调查要根据所要考查的对象的特征灵活选用，一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查．
6．（2分）一个多边形的每一个外角都是45°，则这个多边形的边数为（ ）
A．6B．7C．8D．9
【分析】任意多边形的外角和为360°，用360°除以45°即为多边形的边数．
【解答】解：360°÷45°＝8．
故选：C．
【点评】本题主要考查的是多边形的外角和的应用，明确正多边形的每个外角的度数×边数＝360°是解题的关键．
7．（2分）已知点A与点B关于x轴对称，若点A的坐标为（﹣1，3），点B的坐标为（﹣1，b），则b的值等于（ ）
A．﹣3B．﹣1C．1D．3
【分析】根据关于x轴对称的点，横坐标相同，纵坐标互为相反数，先求出b的值即可．
【解答】解：∵点A（﹣1，3）关于x轴对称的点B的坐标为（﹣1，b），
∴b＝﹣3，
故选：A．
【点评】本题考查了关于x轴对称的点的坐标，利用关于x轴对称的点的横坐标相等，纵坐标互为相反数是解题关键．
8．（2分）在函数y＝中，自变量x的取值范围是（ ）
A．x≠3B．x≥0C．x≥3D．x＞3
【分析】根据被开方数大于等于0列式计算即可得解．
【解答】解：由题意得，x﹣3≥0，
解得x≥3．
故选：C．
【点评】本题考查了函数自变量的范围，一般从三个方面考虑：
（1）当函数表达式是整式时，自变量可取全体实数；
（2）当函数表达式是分式时，考虑分式的分母不能为0；
（3）当函数表达式是二次根式时，被开方数非负．
9．（2分）某校有500名学生参加体育测试，其成绩在25﹣30分之间的有300人，则在25﹣30分之间的频率是（ ）
A．0.6B．0.5C．0.3D．0.1
【分析】根据频率＝频数÷总数，进行计算即可．
【解答】解：根据题意，得：在25﹣30分之间的频率是300÷500＝0.6．
故选：A．
【点评】此题考查了频数与频率，掌握频率的正确计算方法：频率＝频数÷总数是解题的关键．
10．（2分）已知正比例函数y＝kx（k≠0）的函数值随x的增大而增大，则一次函数y＝x+2k的图象大致是（ ）
A．B．
C．D．
【分析】先根据正比例函数y＝kx（k是常数，k≠0）的函数值y随x的增大而增大判断出k的符号，再根据一次函数的图象与系数的关系即可得出结论．
【解答】解：∵正比例函数y＝kx（k是常数，k≠0）的函数值y随x的增大而增大，
∴k＞0，
∵一次函数y＝x+2k，
∴k′＝1＞0，b＝2k＞0，
∴此函数的图象经过一、二、三象限．
故选：A．
【点评】本题主要考查一次函数的图象与系数的关系，掌握y＝kx+b（k≠0）的图象与系数的关系是解题的关键．
当k＞0，b＞0时，图象过一、二、三象限，
当k＞0，b＜0时，图象过一、三、四象限，
当k＜0，b＞0时，图象过一、二、四象限，
当k＜0，b＜0时，图象过二、三、四象限．
11．（2分）关于▱ABCD的叙述，正确的是（ ）
A．若AC＝BD，则▱ABCD是菱形
B．若AB＝AD，则▱ABCD是矩形
C．若AB⊥BC，则▱ABCD是正方形
D．若AC⊥BD，则▱ABCD是菱形
【分析】由菱形的判定方法、矩形的判定方法、正方形的判定方法得出选项A、B、D错误，C正确；即可得出结论．
【解答】解：∵▱ABCD中，AC＝BD，
∴四边形ABCD是矩形，选项A不符合题意；
∵▱ABCD中，AB＝AD，
∴四边形ABCD是菱形，不一定是正方形，选项B不符合题意；
∵▱ABCD中，AB⊥BC，
∴四边形ABCD是矩形，不一定是正方形，选项C不符合题意；
∵▱ABCD中，AC⊥BD，
∴四边形ABCD是菱形，选项D符合题意；
故选：D．
【点评】本题考查了平行四边形的性质、菱形的判定方法、矩形的判定方法、正方形的判定方法；熟练掌握矩形、菱形、正方形的判定方法是解决问题的关键．
12．（2分）对于函数y＝﹣x+3，下列结论正确的是（ ）
A．当x＞4时，y＜0
B．它的图象经过第一、二、三象限
C．它的图象必经过点（﹣1，3）
D．y的值随x值的增大而增大
【分析】根据一次函数的性质和一次函数图象上点的坐标特征可以判断各个选项是否正确，从而可以解答本题．
【解答】解：A．当x＞4时，y＜0，符合题意；
B．它的图象经过第一、二、四象限，不符合题意；
C．它的图象必经过点（﹣1，4），不符合题意；
D．y的值随x值的增大而减小，不符合题意；
故选：A．
【点评】本题考查一次函数的性质和一次函数图象上点的坐标特征，解答本题的关键是明确题意，利用一次函数的性质解答．
13．（2分）如图所示，在矩形ABCD中，点E是对角线AC，BD的交点，点F是边AD的中点且AB＝8，BC＝6，则△DEF的周长是（ ）
A．10B．12C．14D．24
【分析】根据勾股定理得出DB的长，再利用三角形中位线定理和三角形周长解答即可．
【解答】解：∵矩形ABCD，AB＝8，BC＝6，
∴DB＝10，
∵点E是对角线AC，BD的交点，点F是边AD的中点，
∴EF＝＝4，
∴△DEF的周长＝4+5+3＝12，
故选：B．
【点评】此题考查了矩形的性质、三角形的中位线定理．关键是根据勾股定理得出DB的长．
14．（2分）如图6×6的正方形网格放置在平面直角坐标系中，每个小正方形的顶点称为格点．每个小正方向的边长都是1，正方形ABCD的顶点都在格点上，若直线y＝kx（k≠0）与正方形ABCD有公共点，则k不可能是（ ）
A．1B．C．3D．2
【分析】结合图形找出点A、C的坐标，分别将其代入正比例函数解析式中求出k值，进而可找出k的取值范围，对照四个选项即可得出结论．
【解答】解：观察图形可知，点A（1，2），点C（2，1），
当直线y＝kx过点A时，有2＝k；
当直线y＝kx过点C时，有1＝2k，解得：k＝．
∴若直线y＝kx（k≠0）与正方形ABCD有公共点，≤k≤2．
故选：C．
【点评】本题考查了两条直线相交或平行问题以及一次函数图象上点的坐标特征，由点A、C的坐标找出k的取值范围是解题的关键．
15．（2分）如图，把矩形ABCD沿EF翻折，使点B恰好落在AD边的B'处，若矩形的面积为9，AE＝B'D．∠EFB＝60°，则线段BE的长是（ ）
A．B．3C．D．6
【分析】由矩形的性质得出AD∥BC，由平行线的性质得出∠DEF＝∠EFB＝60°，由翻折的性质得出∠EFB＝∠EFB′＝60°，∠B＝∠A′B′F＝90°，∠A＝∠A′＝90°，AE＝A′E，AB＝A′B′，由三角形内角和定理得出∠EB′F＝60°，在Rt△A′EB′中，∠A′B′E＝∠A′B′F﹣∠EB′F＝30°，则B′E＝2A′E，推出AD＝4A′E，AB＝A′B′＝＝＝A′E，由AD•AB＝4A′E×A′E＝9，求出A′E＝，得出AE＝，AB＝，由勾股定理得出BE＝＝3，即可得出结果．
【解答】解：连接BE，如图所示：
∵四边形ABCD是矩形，
∴AD∥BC，
∴∠DEF＝∠EFB＝60°，
∵把矩形ABCD沿EF翻折，点B恰好落在AD边的B′处，
∴∠EFB＝∠EFB′＝60°，∠B＝∠A′B′F＝90°，∠A＝∠A′＝90°，AE＝A′E，AB＝A′B′，
∴∠EB′F＝180°﹣∠DEF﹣∠EFB′＝180°﹣60°﹣60°＝60°，
Rt△A′EB′中，∠A′B′E＝∠A′B′F﹣∠EB′F＝90°﹣60°＝30°，
∴B′E＝2A′E，
∵AE＝B'D＝A′E，
∴AD＝4A′E，AB＝A′B′＝＝＝A′E，
∵矩形ABCD的面积为9，
∴AD•AB＝4A′E×A′E＝9，
解得：A′E＝，
∴AE＝，AB＝，
BE＝＝＝3，
故选：B．
【点评】本题考查了翻折的性质、矩形的性质、勾股定理、含30°角直角三角形的性质、三角形面积与矩形面积的计算等知识，熟练掌握翻折的性质是解题的关键．
16．（2分）如图，在边长为2的正方形ABCD中剪去一个边长为1的小正方形EFGD，动点P从点A出发，沿A→E→F→G→C→B的路线，绕多边形的边匀速运动到点B时停止，则△ABP的面积S随着时间t变化的函数图象大致是（ ）
A．B．
C．D．
【分析】用面积公式计算出点P在线段运动的函数表达式，即可求解．
【解答】解：①当点P在AE上运动时，S＝×AB×AP＝2×t＝t；
②当点P在EF上运动时，S＝×1×2＝1；
③当点P在FG上运动时，S＝×（t﹣1）＝t﹣1；
④当点P在GC上运动时，同理S＝2；
⑤当点P在BC上运动时，同理可得：函数的表达式为一次函数，图象为线段；
故选：B．
【点评】本题是运动型综合题，解题关键是深刻理解动点的函数图象，了解图象中关键点所代表的实际意义，理解动点的完整运动过程．
二、准确填空（本大题共3个小题，17、18每小题3分，19题每空2分，共10分，）
17．（3分）点P（2，4）到y轴的距离是 2
【分析】根据点到y轴的距离等于横坐标的绝对值解答．
【解答】解：点P（2，4）到y轴的距离为2．
故答案为：2．
【点评】本题考查了点的坐标，熟记点到x轴的距离等于纵坐标的绝对值，到y轴的距离等于横坐标的绝对值是解题的关键．
18．（3分）已知直线y＝ax+b与y＝x交于点P（﹣4，﹣2），则关于x，y的二元一次方程组的解是 ．
【分析】直接根据函数图象交点坐标为两函数解析式组成的方程组的解得到答案．
【解答】解：∵直线y＝ax+b和直线y＝x交点P的坐标为（﹣4，﹣2），
∴关于x，y的二元一次方程组的解是．
故答案为．
【点评】本题考查了一次函数与二元一次方程（组）：函数图象交点坐标为两函数解析式组成的方程组的解．
19．（4分）如图，将矩形ABCD在直线上按顺时针方向无滑动翻滚，可依次得到矩形A1B1C1D1，矩形A2B2C1D1矩形A3B2C2D2，…，若AB＝2，BC＝4，那么AA3的长为 12 ，AA15的长为 60 ．
【分析】根据图形和AB＝2，BC＝4，可以求得AA3的长，再根据题意，可以求得AA15的长，本题得以解决．
【解答】解：∵AB＝2，BC＝4，
∴AA3的长为：4+2+4+2＝12，
AA15的长为：（15÷3）×12＝5×12＝60，
故答案为：12，60．
【点评】本题考查图形的变化类，解答本题的关键是明确题意，利用数形结合的思想解答．
三、挑战技能（本大题共4个小题，20、21题每题6分，22、23题每题8分，共28分）
20．（6分）如图表示的是热带风暴从发生到结束的全过程．请结合图象回答下列问题：
（1）热带风暴从开始发生到结束共经历了 16 个小时；
（2）从图象上看，风速在 2～5 （小时）时间段内增大的最快，最大风速是 54 千米/小时；
（3）风速从开始减小到最终停止，平均每小时减小多少千米？
【分析】（1）根据函数图象中的数据可以直接写出热带风暴从开始发生到结束共经历了多长时间；
（2）根据函数图象可以得到风速在哪个时间段内增大的最快，最大风速是多少千米/小时；
（3）根据函数图象中的数据可以计算出风速从开始减小到最终停止，平均每小时减小多少千米．
【解答】解：（1）由图象可得，
热带风暴从开始发生到结束共经历了16个小时，
故答案为：16；
（2）从图象上看，风速在2～5（小时）时间段内增大的最快，最大风速是54千米/小时，
故答案为：2～5，54；
（3）风速从开始减小到最终停止，平均每小时减小：54÷（16﹣10）＝54÷6＝9（千米/小时），
即风速从开始减小到最终停止，平均每小时减小9千米/小时．
【点评】本题考查函数图象，解答本题的关键是明确题意，利用数形结合的思想解答．
21．（6分）如图，已知网格线是由边长为1的小正方形组成，△A′B′C′是由△ABC平移得到的，建立适当的平面直角坐标系后，C点坐标为（1，2）
（1）请在图中画出这个平面直角坐标系；
（2）根据（1）中建立的平面直角坐标系，点A′，B′，C′的坐标分别是A′ （﹣1，0） B′ （2，4） C′ （﹣1，3） ；
（3）若△ABC内点P的坐标为（a，b），写出平移后点P的对应点P′的坐标．
【分析】（1）首先根据C点坐标确定原点位置，再画出坐标系即可；
（2）利用坐标系可直接得到点A′，B′，C′的坐标；
（3）根据△A′B′C′位置可得△ABC的平移方法，进而可得点P的对应点P′坐标．
【解答】解：（1）如图所示；
（2）A′（﹣1，0），B′（2，4），C′（﹣1，3），
故答案为：（﹣1，0），（2，4），（﹣1，3）；
（3）△ABC向上平移1个单位，向左平移2个单位到△A′B′C′的位置，
故点P的对应点P′的坐标为（a﹣2，b+1）．
【点评】此题主要作图﹣﹣平移变换，关键是掌握图形的平移方向、平移距离．
22．（8分）某中学计划根据学生的兴趣爱好组建课外兴趣小组，并随机抽取了部分同学的兴趣爱好进行调查，将收集的数据整理并绘制成下列两幅统计图，请根据图中的信息，完成下列问题：
（1）学校这次调查共抽取了 100 名学生；
（2）求m的值并补全条形统计图；
（3）在扇形统计图，“围棋”所在扇形的圆心角度数为 36° ；
（4）设该校共有学生1000名，请你估计该校有多少名学生喜欢足球．
【分析】（1）用“围棋”的人数除以其所占百分比可得；
（2）用总人数乘以“书法”人数所占百分比求得其人数，据此即可补全图形；
（3）用360°乘以“围棋”人数所占百分比即可得；
（4）用总人数乘以样本中“足球”人数所占百分比可得．
【解答】解：（1）学校本次调查的学生人数为10÷10%＝100名，
故答案为：100；
（2）m＝100﹣25﹣25﹣20﹣10＝20，
∴“书法”的人数为100×20%＝20人，
补全图形如下：
（3）在扇形统计图中，“围棋”所在扇形的圆心角度数为360°×10%＝36°，
故答案为：36°；
（4）估计该校喜欢足球的学生人数为1000×25%＝250人．
【点评】本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．也考查了用样本估计总体的思想．
23．（8分）学校计划购买一批标有单价为3000元的某型号电脑，需要数量在10至20台之间，以下是甲、乙两个商家的优惠政策，学校购买哪家的电脑更合算呢？
优惠政策：
甲店：每台八折．
乙店：先赠一台，其余每台九折．
【分析】首先设买电脑x台，根据题意表示出在两个公司的花费情况，在甲店花费是：3000x×80%＝2400x（元），在乙店花费是：3000（x﹣1）×90%＝2700x﹣2700（元），再根据合算则花费少可得不等式，解不等式即可．
【解答】解：设买电脑x台，则在甲店花费：3000x×80%＝2400x（元），
在乙店花费：3000（x﹣1）×90%＝2700x﹣2700（元）
如果在甲店买合算，则2400x＜2700x﹣2700，
解得：x＞9；
如果在乙店买合算，则2400x＞2700x﹣2700，
解得：x＜9；
如果花费一样：2400x＝2700x﹣2700，
解得：x＝9．
学校购买的数量大于9台，所以去甲店买更合算．
【点评】本题考查了一元一次不等式的应用，关键是根据题意表示出在两个店内的花费情况．
四、能力展示（本大题共2个小题，24题9分、25题10分，共19分）
24．（9分）如图1，△ABC中，AB＝AC，点D（不与点B重合）在BC上，点E是AB的中点，过点A作AF∥BC交DE延长线于点F
（1）求证：△AEF≌△BED；
（2）小明在完成（1）的证明后继续探索，连接AD，BF，如图2所示，并提出猜想，你觉得小明的猜想正确吗？请说明理由．
小明：如果AD平分∠BAC，那么四边形AFBD是矩形．
【分析】（1）根据AAS或ASA证全等即可；
（2）根据对角线互相平分的证明四边形AFBD是平行四边形，再根据等腰三角形三线合一证明∠ADB＝90°，进而根据有一个角是直角的平行四边形是矩形得证．
【解答】证明：（1）∵AF∥BC，
∴∠AFE＝∠EDB，
∵E为AB的中点，
∴EA＝EB，
在△AEF和△BED中，，
∴△AEF≌△BED（ASA）；
（2）∵△AEF≌△BED，
∴AF＝BD，
∵AF∥BD，
∴四边形AFBD是平行四边形，
∵AB＝AC，AD平分∠BAC，
∴AD⊥BD，
∴四边形AFBD是矩形．
【点评】本题考查了矩形的判定，三角形全等的判定及性质，能够了解矩形的判定定理是解答本题的关键，难度不大．
25．（10分）甲、乙两车间同时开始加工一批零件，从开始加工到加工完这批零件，甲车间工作了10个小时，乙车间在中间停工一段时间维修设备，然后按停工前的共作效率继续加工，直到与甲车间同时完成这批零件的加任务为止．设甲、乙两车间各自加工零件的数量为y（个），甲车间加工的时间为x（时），y与x之间的函数图象如图所示．
（1）甲车间每小时加工零件的个数为 75 个；这批零件的总个数为 1110 个；
（2）求乙车间维护设备后，乙车间加工零件的数量y与x之间的函数关系式；
（3）在加工这批零件的过程中，当甲、乙两车间共同加工完930个零件时，求甲车间的时间．
【分析】（1）根据工作效率＝工作总量÷工作时间，即可求出甲车间每小时加工零件件数，再根据乙车间停工前后的作效率不变求出乙加工的件数即可解答；
（2）根据待定系数法，即可求出乙车间维修设备后，乙车间加工零件数量y与x之间的函数关系式；
（3）根据加工的零件总件数＝工作效率×工作时间，求出甲车间加工零件数量y与x之间的函数关系式，将甲、乙两关系式相加令其等于930，求出x值，此题得解．
【解答】解：（1）甲车间每小时加工零件件数为750÷10＝75（件），
这批零件的总件数为750+90÷2×（10﹣4+2）＝1110（件）．
故答案为：75；1110．
（2）设乙车间维护设备后，乙车间加工零件的数量y与x之间的函数关系式y＝kx+b，
由图象经过（4，90）与（10，360）两点可得，
，解得，
所以y＝45x﹣90；
（3）甲车间加工零件数量y与x之间的函数关系式为y＝75x，
当75x+45x﹣90＝930时，x＝8.5．
答：甲、乙两车间共同加工完930件零件时甲车间所用的时间为8.5小时．
【点评】本题考查了一次函数的应用以及解一元一次方程，解题的关键是：（1）根据数量关系，列式计算；（2）根据数量关系，找出乙车间维修设备后，乙车间加工服装数量y与x之间的函数关系式；（3）根据数量关系，找出甲车间加工服装数量y与x之间的函数关系式．
五、挑战自我（本大题11分）
26．（11分）如图1所示，把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起，使三角板的直角顶点和正方形的顶点C重合，点E，F分别在正方形的边CB，CD上，连接AE、AF．
（1）求证：AE＝AF；
（2）取AF的中点M，EF的中点N，连接MD，MN．则MD，MN的数量关系是 MD＝MN ，MD、MN的位置关系是 MD⊥MN
（3）将图2中的直角三角板ECF，绕点C旋转180°，图3所示，其他条件不变，则（2）中的两个结论还成立吗？若成立，请加以证明；若不成立，请说明理由．
【分析】（1）根据正方形的性质以及等腰直角三角形的知识证明出CE＝CF，继而证明出△ABE≌△ADF，得到AE＝AF，证明出△AEF是等腰三角形；
（2）DM、MN的数量关系是相等，位置关系式垂直，理由三角形的中位线定理，直角三角形斜边中线的性质即可解决问题．
（3）连接AE，交MD于点G，标记出各个角，首先证明出MN∥AE，MN＝AE，再有（1）的结论以及角角之间的数量关系得到∠DMN＝∠DGE＝90°．
【解答】（1）证明：如图1中，
∵四边形ABCD是正方形
∴AB＝AD＝BC＝CD，∠B＝∠ADF＝90°，
∵△CEF是等腰直角三角形，∠C＝90°，
∴CE＝CF，
∴BC﹣CE＝CD﹣CF，
即BE＝DF，
∴△ABE≌△ADF（SAS），
∴AE＝AF．
（2）解：如图2中，结论：相等，垂直；
理由：∵在Rt△ADF中DM是斜边AF的中线，
∴AF＝2DM，
∵MN是△AEF的中位线，
∴AE＝2MN，
∵AE＝AF，
∴DM＝MN；
∵∠DMF＝∠DAF+∠ADM，AM＝MD，
∵∠FMN＝∠FAE，∠DAF＝∠BAE，
∴∠ADM＝∠DAF＝∠BAE，
∴∠DMN＝∠BAD＝90°，
∴DM⊥MN；
（3）如图3中，（2）中的两个结论还成立，
理由：连接AE，交MD于点G．
∵点M为AF的中点，点N为EF的中点，
∴MN∥AE，MN＝AE，
由（1）同理可证，
AB＝AD＝BC＝CD，∠B＝∠ADF，CE＝CF，
又∵BC+CE＝CD+CF，即BE＝DF，
∴△ABE≌△ADF（SAS），
∴AE＝AF，
在Rt△ADF中，
∵点M为AF的中点，
∴DM＝AF，
∴DM＝MN，
∵△ABE≌△ADF，
∴∠1＝∠2，
∵AB∥DF，
∴∠1＝∠3，
同理可证：∠2＝∠4，
∴∠3＝∠4，
∵DM＝AM，
∴∠MAD＝∠5，
∴∠DGE＝∠5+∠4＝∠MAD+∠3＝90°，
∵MN∥AE，
∴∠DMN＝∠DGE＝90°，
∴DM⊥MN．
【点评】本题属于四边形综合题，主要考查正方形的性质以及全等三角形的判定与性质等知识点，解答本题的关键是利用好各小题之间的联系，此题难度不大，但是角角之间的数量关系有点复杂，请同学们解答的时候注意．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布
日期：2021/6/15 11:19:07；用户：13784622801；邮箱：13784622801；学号：37960971