初中数学北师大版九年级下册第二章 二次函数综合与测试复习课件ppt

这是一份初中数学北师大版九年级下册第二章 二次函数综合与测试复习课件ppt，共24页。PPT课件主要包含了二次函数的定义，随堂练习，二次函数的图象与性质，抛物线的平移，平移关系，yax2，yax－h2，当h0时向右平移，当h0时向左平移，当k0时向上平移等内容，欢迎下载使用。

定义：一般地，形如 y=ax²+bx+c (a，b，c是常数，a≠ 0)的函数叫做x的二次函数.
（1）关于x的代数式一定是整式，a，b，c为常数，且a≠0；
（2）等式的右边最高次数为2，可以没有一次项和常数项，但不能没有二次项.
1. 下列函数中，哪些是二次函数？
（1）y＝3(x－1)²＋1 （2）
（5） y＝(x＋3)²－x² .
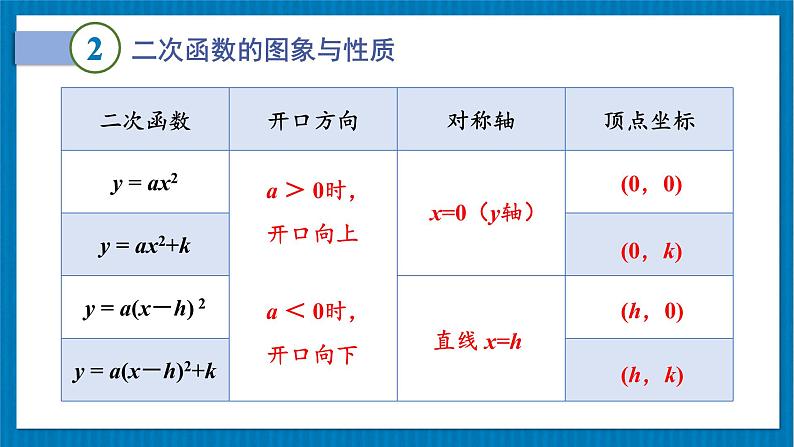
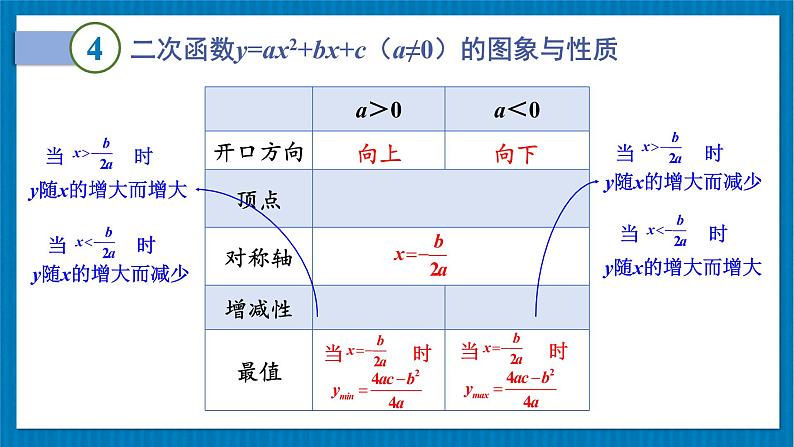
a ＞ 0时，开口向上
a ＜ 0时，开口向下
y=a(x－h)2+k
可概括为：左加右减，上加下减.
2. 将抛物线y=x2+2x－3向左平移4个单位长度，再向下平移3个单位长度，求平移后所得抛物线的解析式.
顶点式 y=(x+1)2－4
二次函数y=ax2+bx+c（a≠0）的图象与性质
3. 若无论x取何实数，二次函数y=ax2+bx+c的值总为负，那么a、c应满足的条件是（ ） A. a>0且b2－4ac≥0 B. a>0且b2－4ac>0 C. a<0且b2－4ac<0 D. a<0且b2－4ac ≤0
4. 已知二次函数y=ax2+bx+c的图象如图所示，请根据图象判断下列各式的符号：a___0，b___0， c____0，∆____0，a－b+c___0，a+b+c____0
5. 函数y=ax+b和y=ax2+bx+c在同一直角坐标系内的图象大致是（ ）
二次函数解析式的三种表示方式
2. 已知抛物线顶点坐标（h，k），通常设抛物线解析式为___________________；
3. 已知抛物线与x轴的两个交点(x1，0)、 (x2，0)，通常设解析式为_______________________.
1. 已知抛物线上的三点，通常设解析式为________________；
y=ax2+bx+c(a≠0)
y=a(x－h)2+k(a≠0)
y=a(x－x1)(x－x2) (a≠0)
6. 二次函数y=ax2+bx+c的最大值是2，图象顶点在直线y=x+1上，并且图象经过点（3，－6），求a、b、c.
解：∵二次函数的最大值是2， ∴抛物线的顶点纵坐标为2.
又∵抛物线的顶点在直线y=x+1上，
∴顶点坐标为（ 1 ， 2）.
∴当y=2时，x=1.
设二次函数的解析式为y=a(x－1)2+2，
6. 二次函数y=ax2+bx+c的最大值是2，图象顶点在直线y=x+1上，并且图象经过点（3，－6），求a、b、c。
又∵图象经过点（3，－6），
∴－6=a(3－1)2+2，∴a=－2.
∴ 二次函数的解析式为y=－2(x－1)2+2，
即： y=－2x2+4x.
∴ a=－2、b=4、c=0.
7. 若a+b+c=0，a0，把抛物线y=ax2+bx+c向下平移4个单位，再向左平移5个单位所得到的新抛物线的顶点是(－2，0)，求原抛物线的解析式.
新抛物线向上平移4个单位，向右平移5个单位即得原抛物线.
原抛物线顶点（3,4）
设原抛物线的解析式为y=a(x－3)2+4，
将点（1,0）代入，得a=－1，
∴ 二次函数的解析式为y=－ (x－3)2+4= －x2+6x－5.
8. 如图，假设篱笆(虚线部分)的长度是15m，如何围篱笆才能使其所围成矩形的面积最大?
解：如图，设矩形的一边AB=x m，那么另一边BC=(15-x) m，面积为S m2，则
9. 某旅行社组团去外地旅游，30人起组团，每人单价800元.旅行社对超过30人的团给予优惠，即旅行团每增加一人，每人的单价就降低10元.你能帮助分析一下，当旅行团的人数是多少时，旅行社可以获得最大营业额？
解：设旅行团人数为x人，营业额为y元，则
答：当旅行社的人数是55人时，旅行社可以获得最大的营业额.
二次函数与一元二次方程
二次函数y=ax2+bx+c的图象与x轴的交点的横坐标就是一元二次方程ax2+bx+c=0的根.
利用二次函数求一元二次方程的近似根的一般步骤：
近似根就出现在对应y值正负交换的位置.
利用二次函数求一元二次方程的近似根的一般方法：
10. 已知二次函数y=kx2+(2k-1)x-1与x轴交点的横坐标为x1，x2(x1有关于二次函数的内容，你还有哪些疑惑？