高中数学3.1.3概率的基本性质背景图ppt课件

这是一份高中数学3.1.3概率的基本性质背景图ppt课件，共22页。PPT课件主要包含了〖教学情境设计〗，1包含关系，2相等关系，事件的关系和运算，5互斥事件，6互为对立事件，≤PA≤1，PA1，PA0等内容，欢迎下载使用。

一、事件的关系和运算：
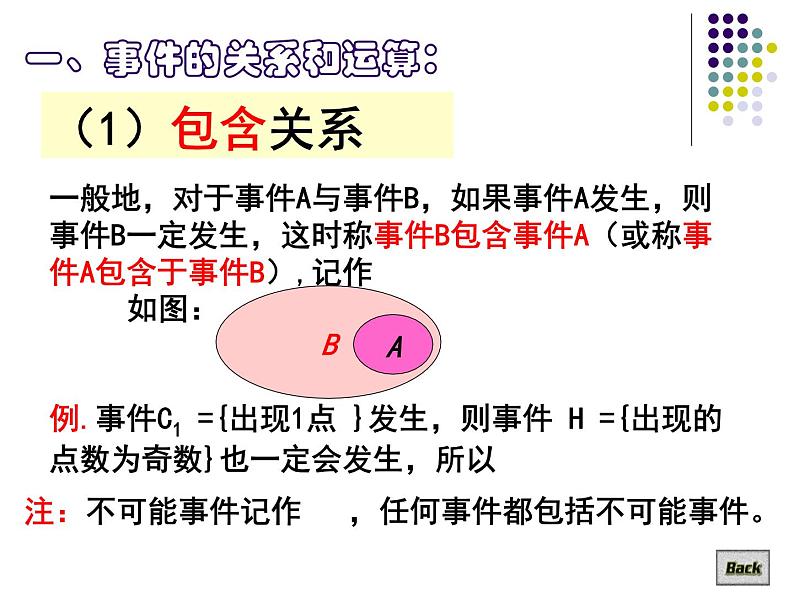
一般地，对于事件A与事件B，如果事件A发生，则事件B一定发生，这时称事件B包含事件A（或称事件A包含于事件B）,记作
例.事件C1={出现1点}发生，则事件D1={出现的点数不大于1}就一定会发生，反过来也一样，所以C1=D1。
（3）并事件（和事件）
若某事件发生当且仅当事件A发生或事件B发生，则称此事件为事件A和事件B的并事件（或和事件），记作 。
例.若事件K={出现1点或5点} 发生，则事件C1 ={出现1点}与事件C5 ={出现 5 点 }中至少有一个会发生，则K .
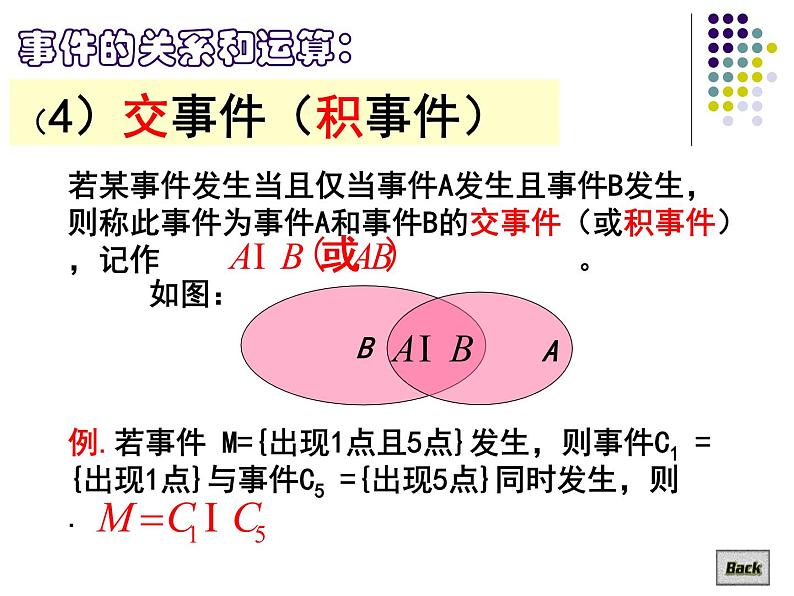
（4）交事件（积事件）
若某事件发生当且仅当事件A发生且事件B发生，则称此事件为事件A和事件B的交事件（或积事件），记作 。
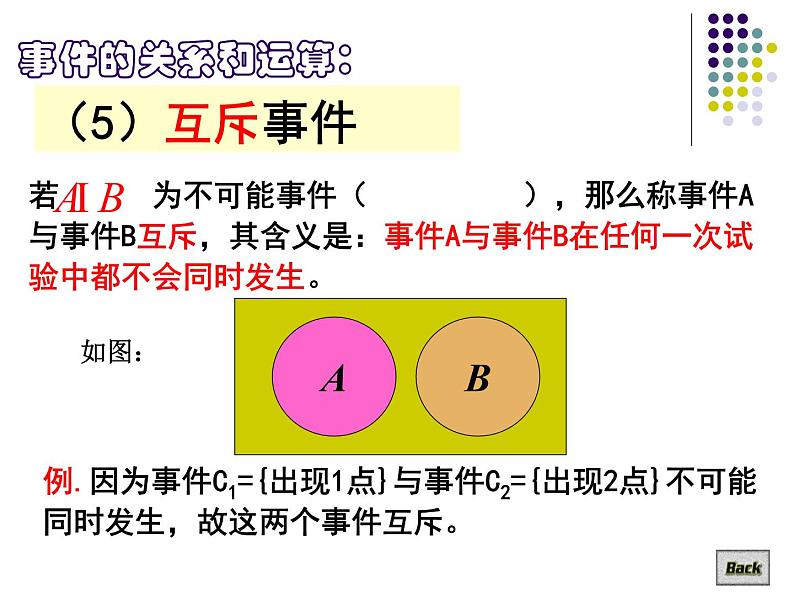
例.因为事件C1={出现1点}与事件C2={出现2点}不可能同时发生，故这两个事件互斥。
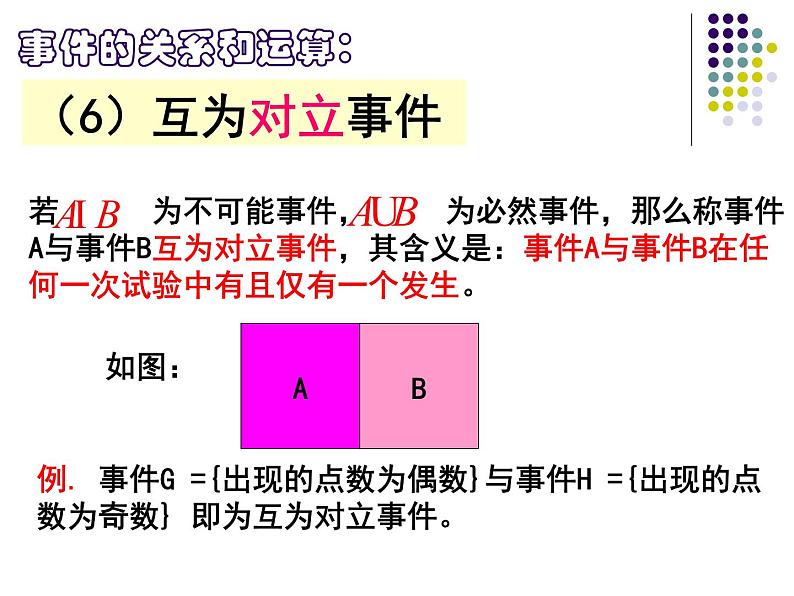
例. 事件G ={出现的点数为偶数}与事件H ={出现的点数为奇数} 即为互为对立事件。
互斥事件与对立事件的区别与联系:互斥事件是指事件A与事件B在一次试验中不会同时发生，其具体包括三种不同的情形：（1）事件A发生且事件B不发生；（2）事件A不发生且事件B发生；（3）事件A与事件B同时不发生.对立事件是指事件A与事件B有且仅有一个发生，其包括两种情形；（1）事件A发生且B不发生；（2）事件B发生事件A不发生.对立事件是互斥事件的特殊情形。
例题分析：例1 一个射手进行一次射击,试判断下列事件哪些是互斥事件?哪些是对立事件?事件A：命中环数大于7环； 事件B：命中环数为10环；事件C：命中环数小于6环； 事件D：命中环数为6、7、8、9、10环.
分析：要判断所给事件是对立还是互斥，首先将两个概念的联系与区别弄清楚，互斥事件是指不可能同时发生的两事件，而对立事件是建立在互斥事件的基础上，两个事件中一个不发生，另一个必发生。
解:互斥事件有:A和C、B和C、C和D. 对立事件有:C和D.
练习：从1，2，…，9中任取两个数，其中 （1）恰有一个是偶数和恰有一个是奇数； （2）至少有一个是奇数和两个数都是奇数； （3）至少有一个奇数和两个都是偶数； （4）至少有一个偶数和至少有一个奇数。 在上述事件中是对立事件的是 （ ） A.(1) B.(2) (4) C.(3) D.(1) (3)
练习：判断下列给出的每对事件，是否为互斥事件，是否为对立事件，并说明理由。 从40张扑克牌（红桃，黑桃，方块，梅花点数从1-10各10张）中，任取一张。 （1）“抽出红桃”与“抽出黑桃”； （2）“抽出红色牌”与“抽出黑色牌”； （3）“抽出的牌点数为5的倍数”与“抽出的牌点数大于9”。
是互斥事件，不是对立事件
既是互斥事件，又是对立事件
不是互斥事件，也不是对立事件
【二】.概率的几个基本性质:
(1)任何事件的概率在0~1之间,即
(2)必然事件的概率为1,即
(3)不可能事件的概率为0,即
(4)如果事件A与事件B互斥,则 P(A∪B)=P(A)+P(B)
(5)如果事件B与事件A是互为对立事件,则 P(B)=1-P(A)
例2 如果从不包括大小王的52张扑克牌中随机抽取一张，那么取到红心（事件A）的概率是0.25，取到方块（事件B）的概率是0.25，问：（1）取到红色牌（事件C）的概率是多少？（2）取到黑色牌（事件D）的概率是多少？
分析：事件C=A∪B，且A与B互斥，因此可用互斥事件的概率和公式求解，事件C与事件D是对立事件，因此P(D)=1-P(C)．
解:(1)P(C)=P(A)+ P(B)=0.25+0.25=0.5; (2)P(D)=1-P(C)=1-0.5=0.5.
例3 甲，乙两人下棋，和棋的概率为1/2，乙获胜的概率为1/3，求：（1）甲获胜的概率；（2）甲不输的概率。
分析：甲乙两人下棋，其结果有甲胜，和棋，乙胜三种，它们是互斥事件。
解（1）“甲获胜”是“和棋或乙胜”的对立事件，所以甲获胜的概率是P=1-1/2-1/3=1/6。
（2）解法1，“甲不输”看作是“甲胜”，“和棋”这两个事件的并事件所以P=1/6+1/2=2/3。解法2，“甲不输”看作是“乙胜”的对立事件，P=1-1/3=2/3。
练习 某射手射击一次射中10环，9环，8环，7环的概率是0.24，0.28，0.19，0.16，计算这名射手射击一次 （1）射中10环或9环的概率； （2）至少射中7环的概率。
（1） P（A∪B）=P（A）+P（B） =0.24+0.28=0.52。
（2） 因为它们是互斥事件，所以至少射中7环的概率是0.24+0.28+0.19+0.16=0.87
练习：某地区的年降水量在下列范围内的概率如下表所示：
（1）求年降水量在[100，200）（mm)范围内的概率；
（2）求年降水量在[150，300）（mm)范围内的概率。
P=0.12+0.25=0.37
P=0.25+0.16+0.14=0.55
例4 袋中有12个小球，分别为红球、黑球、黄球、绿球，从中任取一球，得到红球的概率为1/3，得到黑球或黄球的概率是5/12，得到黄球或绿球的概率也是5/12，试求得到黑球、得到黄球、得到绿球的概率各是多少？
分析：利用方程的思想及互斥事件、对立事件的概率公式求解．
解：从袋中任取一球，记事件“摸到红球”、“摸到黑球”、“摸到黄球”、“摸到绿球”为A、B、C、D，
则有 P(B∪C)=P(B)+P(C) =5/12;
P(C∪D)=P(C)+P(D) =5/12;
P(B∪C∪D)=P(B)+P(C)+P(D)=1-P(A) =1-1/3=2/3;
解的P(B)=1/4,P(C)=1/6,P(D)=1/4.
答:得到黑球、黄球、绿球的概率分别是1/4,1/6,1/4.
例5. 某公务员去开会，他乘火车、轮船、汽车、飞机去的概率分别为0.3、0.2、0.1、0.4，（1）求他乘火车或乘飞机去的概率；（2）求他不乘轮船去的概率；（3）如果他乘某种交通工具去开会的概率为0.5，请问他有可能是乘何种交通工具去的？
解：记“他乘火车去”为事件A，，“他乘轮船去”为事件B，“他乘汽车去”为事件C，“他乘飞机去”为事件D，这四个事件不可能同时发生，故它们彼此互斥， （1）故P(A∪D)=0.7； （2）设他不乘轮船去的概率为P，则P=1－P(B)=0.8； （3）由于0.5=0.1+0.4=0.2+0.3，故他有可能乘火车或乘轮船去，也有可能乘汽车或乘飞机去。
四、课堂小结1.概率的基本性质：1）必然事件概率为1，不可能事件概率为0， 因此0≤P(A)≤1；2）当事件A与B互斥时，满足加法公式： P(A∪B)= P(A)+ P(B)；3）若事件A与B为对立事件，则A∪B为必然事件，所以P(A∪B)= P(A)+ P(B)=1，于是有 P(A)=1-P(B)；