人教版2021年八年级上册第11-13章期中复习综合训练卷 解析版

这是一份人教版2021年八年级上册第11-13章期中复习综合训练卷 解析版，共13页。试卷主要包含了下列说法错误的是，在平面直角坐标系中，点A等内容，欢迎下载使用。
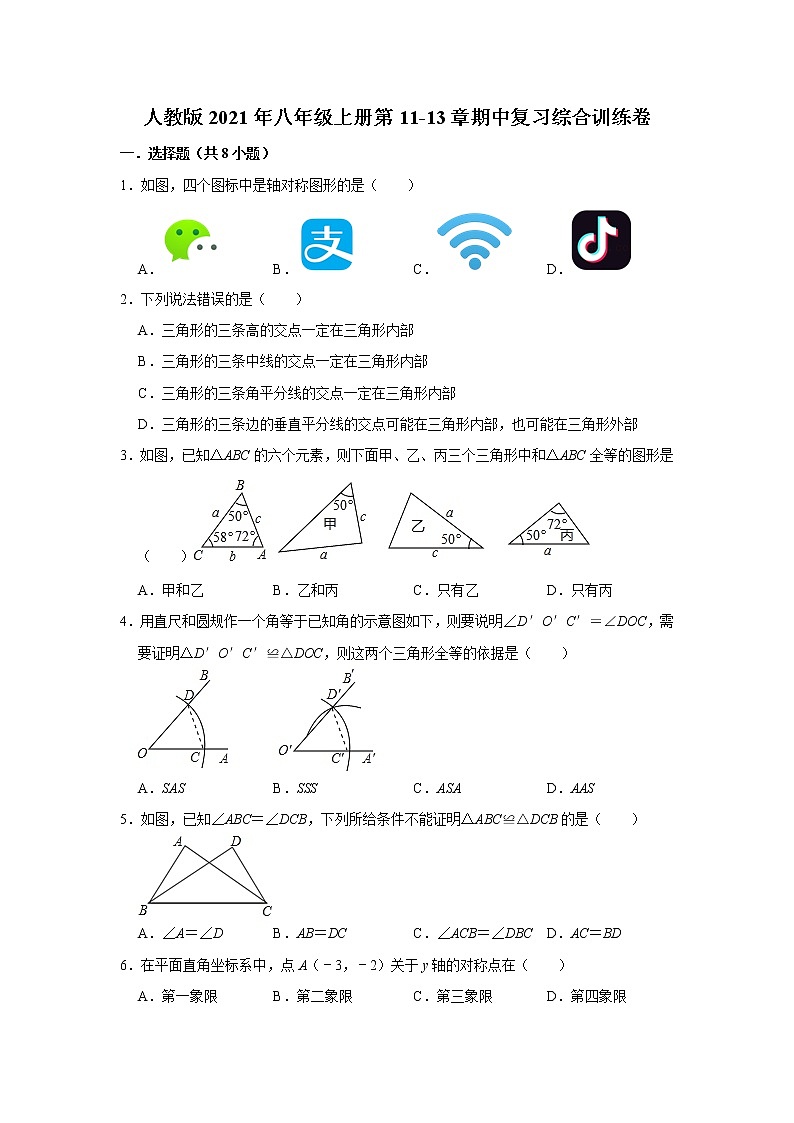
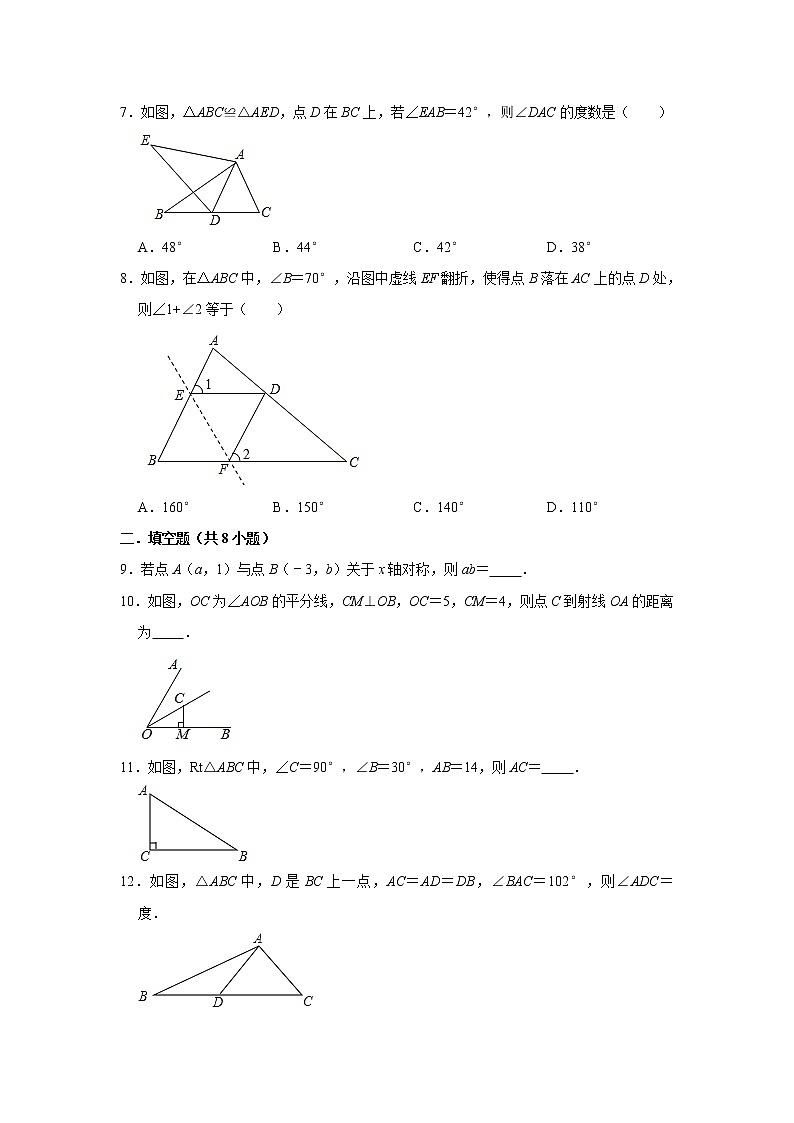
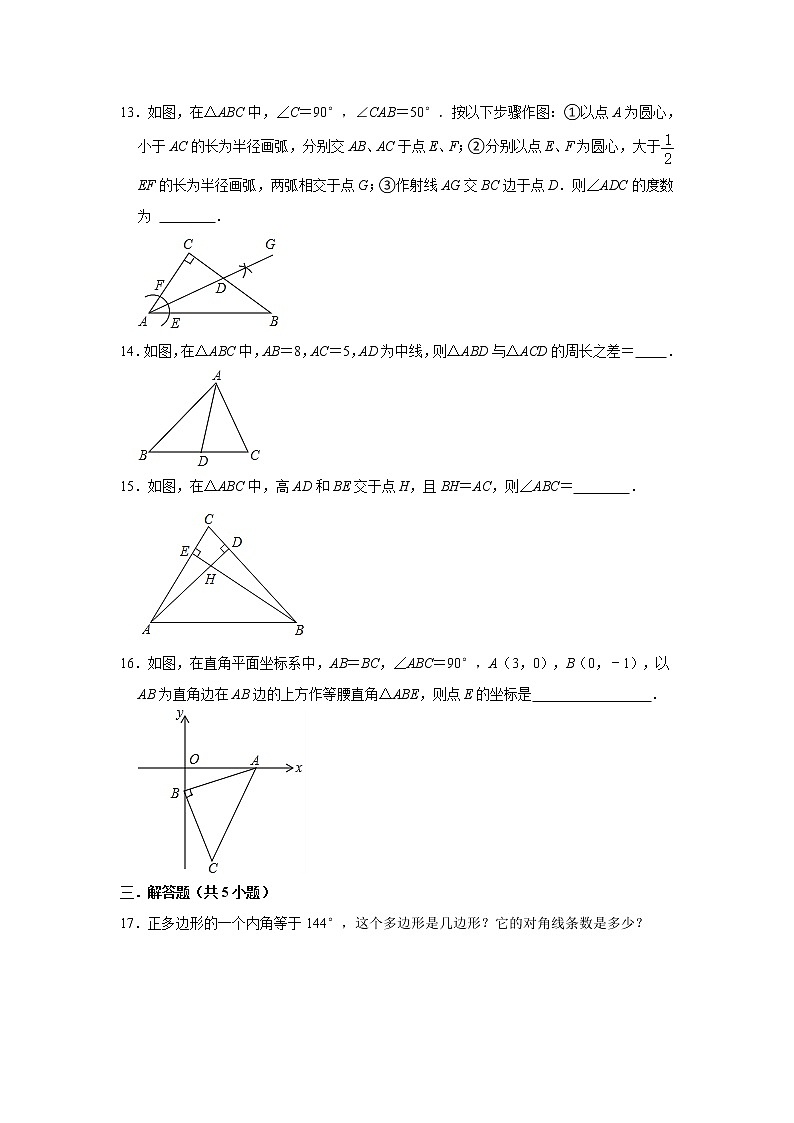
人教版2021年八年级上册第11-13章期中复习综合训练卷一．选择题（共8小题）1．如图，四个图标中是轴对称图形的是（　　）A． B． C． D．2．下列说法错误的是（　　）A．三角形的三条高的交点一定在三角形内部 B．三角形的三条中线的交点一定在三角形内部 C．三角形的三条角平分线的交点一定在三角形内部 D．三角形的三条边的垂直平分线的交点可能在三角形内部，也可能在三角形外部3．如图，已知△ABC的六个元素，则下面甲、乙、丙三个三角形中和△ABC全等的图形是（　　）A．甲和乙 B．乙和丙 C．只有乙 D．只有丙4．用直尺和圆规作一个角等于已知角的示意图如下，则要说明∠D′O′C′＝∠DOC，需要证明△D′O′C′≌△DOC，则这两个三角形全等的依据是（　　）A．SAS B．SSS C．ASA D．AAS5．如图，已知∠ABC＝∠DCB，下列所给条件不能证明△ABC≌△DCB的是（　　）A．∠A＝∠D B．AB＝DC C．∠ACB＝∠DBC D．AC＝BD6．在平面直角坐标系中，点A（﹣3，﹣2）关于y轴的对称点在（　　）A．第一象限 B．第二象限 C．第三象限 D．第四象限7．如图，△ABC≌△AED，点D在BC上，若∠EAB＝42°，则∠DAC的度数是（　　）A．48° B．44° C．42° D．38°8．如图，在△ABC中，∠B＝70°，沿图中虚线EF翻折，使得点B落在AC上的点D处，则∠1+∠2等于（　　）A．160° B．150° C．140° D．110°二．填空题（共8小题）9．若点A（a，1）与点B（﹣3，b）关于x轴对称，则ab＝　 　．10．如图，OC为∠AOB的平分线，CM⊥OB，OC＝5，CM＝4，则点C到射线OA的距离为　 　．11．如图，Rt△ABC中，∠C＝90°，∠B＝30°，AB＝14，则AC＝　 　．12．如图，△ABC中，D是BC上一点，AC＝AD＝DB，∠BAC＝102°，则∠ADC＝　   　度．13．如图，在△ABC中，∠C＝90°，∠CAB＝50°．按以下步骤作图：①以点A为圆心，小于AC的长为半径画弧，分别交AB、AC于点E、F；②分别以点E、F为圆心，大于EF的长为半径画弧，两弧相交于点G；③作射线AG交BC边于点D．则∠ADC的度数为 　    　．14．如图，在△ABC中，AB＝8，AC＝5，AD为中线，则△ABD与△ACD的周长之差＝　 　．15．如图，在△ABC中，高AD和BE交于点H，且BH＝AC，则∠ABC＝　    　．16．如图，在直角平面坐标系中，AB＝BC，∠ABC＝90°，A（3，0），B（0，﹣1），以AB为直角边在AB边的上方作等腰直角△ABE，则点E的坐标是　             　．三．解答题（共5小题）17．正多边形的一个内角等于144°，这个多边形是几边形？它的对角线条数是多少？    18．如图，AB＝AC，∠A＝40°，AB的垂直平分线MN交AC于点D，求∠DBC的度数． 19．尺规作图：如图，在△ABC中．（1）作∠C的角平分线CP交AB于P点．（2）若∠A＝50°，∠B＝60°，求∠CPA的度数．  20．已知在△ABC中，∠CAB的平分线AD与BC的垂直平分线D交于点D，DM⊥AB于M，DN⊥AC的延长线于N．（1）证明：BM＝CN；（2）当∠BAC＝70°时，求∠DCB的度数．   21．已知，如图，△BAC的平分线AD与BC的垂直平分线DG交于点D，过点D的直线DE⊥AB于点E，DF⊥AC于点F．（1）求证：AE＝AF；（2）求证：BE＝CF；（3）若AB＝8cm，AC＝4cm，求AE的长．                   参考答案一．选择题（共8小题）1．解：A、不是轴对称图形，故此选项错误；B、不是轴对称图形，故此选项错误；C、是轴对称图形，符合题意；D、不是轴对称图形，故此选项错误．故选：C．2．解：A、三角形的三条高的交点在三角形内部、外部或顶点上，本选项说法错误，符合题意；B、三角形的三条中线的交点一定在三角形内部，本选项说法正确，不符合题意；C、三角形的三条角平分线的交点一定在三角形内部，本选项说法正确，不符合题意；D、三角形的三条边的垂直平分线的交点可能在三角形内部，也可能在三角形外部，本选项说法正确，不符合题意；故选：A．3．解：图甲不符合三角形全等的判定定理，即图甲和△ABC不全等；图乙符合SAS定理，即图乙和△ABC全等；图丙符合AAS定理，即图丙和△ABC全等；故选：B．4．解：在△D′O′C′和△DOC中，，∴△D′O′C′≌△DOC（SSS），∴∠D′O′C′＝∠DOC．则全等的依据为SSS．故选：B．5．解：A、添加∠A＝∠D可利用AAS判定△ABC≌△DCB，故此选项不合题意；B、添加AB＝DC可利用SAS定理判定△ABC≌△DCB，故此选项不合题意；C、添加∠ACB＝∠DBC可利用ASA定理判定△ABC≌△DCB，故此选项不合题意；D、添加AC＝BD不能判定△ABC≌△DCB，故此选项符合题意；故选：D．6．解：∵点A（﹣3，﹣2）关于y轴的对称点是（3，﹣2），∴A（﹣3，﹣2）关于y轴的对称点在第四象限．故选：D．7．解：∵△ABC≌△AED，∴∠EAD＝∠BAC，∴∠EAB＝∠DAC＝42°．故选：C．8．解：∵∠B＝70°，∴∠BEF+∠BFE＝110°，∵翻折，∴∠BEF＝∠DEF，∠BFE＝∠DFE，∴∠BED+∠BFD＝2（∠BEF+∠BFE）＝2×110°＝220°，∴∠1+∠2＝180°×2﹣220°＝140°，故选：C．二．填空题（共8小题）9．解：∵点A（a，1）与点B（﹣3，b）关于x轴对称，∴a＝﹣3，b＝﹣1，∴ab＝3，故答案为：3．10．解：过C点作CN⊥OA于N，如图，∵OC为∠AOB的平分线，CM⊥OB，CN⊥OA，∴CN＝CM＝4，即点C到射线OA的距离为4．故答案为4．11．解：∵∠C＝90°，∠B＝30°，AB＝14，∴AC＝AB＝×14＝7．故答案为：7．12．解：∵AC＝AD＝DB，∴∠B＝∠BAD，∠ADC＝∠C，设∠ADC＝α，∴∠B＝∠BAD＝，∵∠BAC＝102°，∴∠DAC＝102°﹣，在△ADC中，∵∠ADC+∠C+∠DAC＝180°，∴2α+102°﹣＝180°，解得：α＝52°．故答案为：52．13．解：解法一：连接EF．∵点E、F是以点A为圆心，小于AC的长为半径画弧，分别与AB、AC的交点，∴AF＝AE；∴△AEF是等腰三角形；又∵分别以点E、F为圆心，大于EF的长为半径画弧，两弧相交于点G；∴AG是线段EF的垂直平分线，∴AG平分∠CAB，∵∠CAB＝50°，∴∠CAD＝25°；在△ADC中，∠C＝90°，∠CAD＝25°，∴∠ADC＝65°（直角三角形中的两个锐角互余）； 解法二：根据已知条件中的作图步骤知，AG是∠CAB的平分线，∵∠CAB＝50°，∴∠CAD＝25°；在△ADC中，∠C＝90°，∠CAD＝25°，∴∠ADC＝65°（直角三角形中的两个锐角互余）；故答案是：65°．14．解：∵AD为中线，∴BD＝CD，则C△ABD﹣C△ACD＝（AB+AD+BD）﹣（AC+AD+CD）＝AB+AD+BD﹣AC﹣AD﹣CD＝AB﹣AC＝8﹣5＝3，故答案为：3．15．解：∵△ABC为锐角三角形，∴高AD和BE在三角形内．∵高AD和BE交于点H，∴∠ADC＝∠BEC＝90°．∵∠EBD+∠BHD＝90°，∠AHE+∠HAE＝90°，∠BHD＝∠AHE，∴∠EAD＝∠EBD，又∵BH＝AC，∠ADC＝∠BDH＝90°，∴△BDH≌△ADC（AAS），∴BD＝AD，∵∠ADB＝90°，∴∠ABC＝45°．故答案为45°16．解：如图，作EH⊥y轴于H，CF⊥y轴于F，E′G⊥OA于G．在△AOB和△FBC中，，∴△OAB≌△FBC，∴CF＝OB＝1，BF＝OA＝3，当B为直角顶点时，同理可得EH＝1，BH＝2，∴E（﹣1，2），当A为直角顶点时，同理可得，AG＝1，E′G＝3，∴E′（2，3），综上所述，点E坐标（﹣1，2）或（2，3）．故答案为（﹣1，2）或（2，3）三．解答题（共5小题）17．解：360°÷（180°﹣144°）＝10，即这个多边形是10边形，对角线的总条数是：10×（10﹣3）÷2＝35（条）．18．解：∵AB＝AC，∴∠ABC＝∠ACB＝＝70°，∵MN垂直平分AB，∴DA＝DB，∴∠A＝∠ABD＝40°，∴∠DBC＝∠ABC﹣∠ABD＝70°﹣40°＝30°．故答案为：30°．19．解：（1）如图，CP为所作；（2）∵∠A＝50°，∠B＝60°，∴∠ACB＝180°﹣∠A﹣∠B＝180°﹣50°﹣60°＝70°，∵CP平分∠ACB，∴∠BCP＝∠ACB＝35°，∴∠APC＝∠B+∠BCP＝60°+35°＝95°．20．（1）证明：连接BD，如图所示：∵AD是∠CAB的平分线，DM⊥AB，DN⊥AC，∴DM＝DN，∵DE垂直平分线BC，∴DB＝DC，在Rt△DMB和Rt△DNC中，，∴Rt△DMB≌Rt△DNC（HL），∴BM＝CN；（2）解：由（1）得：∠BDM＝∠CDN，∵AD是∠CAB的平分线，DM⊥AB，DN⊥AC，∴DM＝DN，在Rt△DMA和Rt△DNA中，，∴Rt△DMA≌Rt△DNA（HL），∴∠ADM＝∠ADN，∵∠BAC＝70°，∴∠MDN＝110°，∠ADM＝∠ADN＝55°，∵∠BDM＝∠CDN，∴∠BDC＝∠MDN＝110°，∵DE是BC的垂直平分线，∴DB＝DC，∴∠EDC＝BDC＝55°，∴∠DCB＝90°﹣∠EDC＝35°，∴∠DCB＝35°．21．（1）证明：∵点D在∠BAC的平分线上，DE⊥AB，DF⊥AC，∴DE＝DF．在Rt△AED与Rt△AFD中，，∴Rt△AED≌Rt△AFD（HL），∴AE＝AF；（2）证明：连接BD，CD．∵点D在BC的垂直平分线上，∴DB＝DC；在Rt△DCF与Rt△DBE中，，∴Rt△DCF≌Rt△DBE（HL），∴CF＝BE；（3）解：∵AB＝8cm，AC＝4cm，CF＝BE，AE＝AF＝AC+CF，∴AB＝AE+BE＝AC+BE+CF＝AC+2BE，∴BE＝2cm，∴AE＝AB﹣BE＝6（cm）．