河南省郑州枫杨外国语学校2021-2022学年上学期第一次月考八年级数学【试卷+答案】

这是一份河南省郑州枫杨外国语学校2021-2022学年上学期第一次月考八年级数学【试卷+答案】，共18页。试卷主要包含了选择题，填空题，解答题.等内容，欢迎下载使用。
2021-2022学年河南省郑州市高新区枫杨外国语学校八年级第一学期第一次月考数学试卷
一、选择题（每题3分，共30分）
1．在下列实数3.1415926，，，，，中无理数的个数有（　　）
A．2个 B．3个 C．4个 D．5个
2．下面四组数，其中是勾股数的一组是（　　）
A．32，42，52 B．0.3，0.4，0.5
C．3，4，5 D．6，7，8
3．的算术平方根为（　　）
A．9 B．±9 C．3 D．±3
4．若﹣，且x是整数，则满足条件的x值有（　　）
A．5个 B．4个 C．3个 D．2个
5．满足下列条件的△ABC，不是直角三角形的是（　　）
A．b2＝c2﹣a2 B．a：b：c＝3：4：5
C．∠C＝∠A﹣∠B D．∠A：∠B：∠C＝12：13：15
6．要使有意义，x的取值范围是（　　）
A．x≥2021 B．x≤2021 C．x＞2021 D．x＜2021
7．已知实数a在数轴上的对应点位置如图，则化简的结果是（　　）

A．2a﹣3 B．﹣1 C．1 D．3﹣2a
8．如图，一棵大树在离地面6m，10m两处折成三段，中间一段AB恰好与地面平行，大树顶部落在离大树底部12m处，则大树折断前的高度是（　　）

A．14m B．16m C．18m D．20m
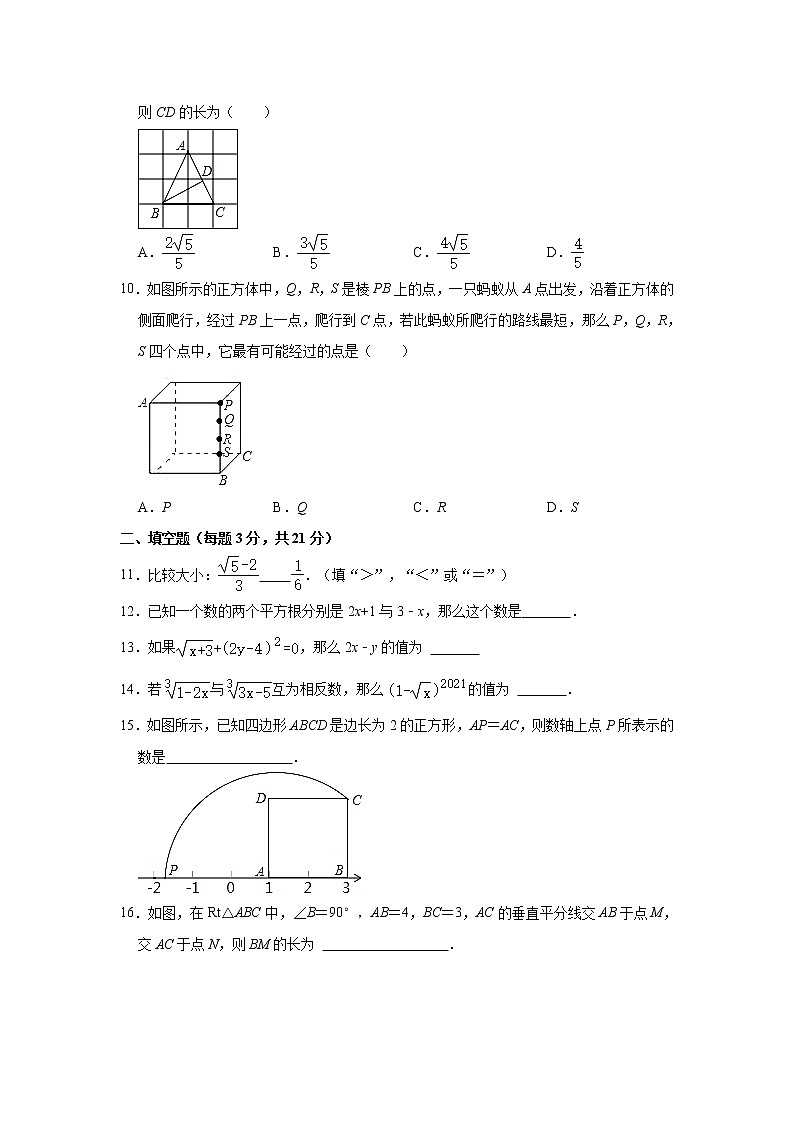
9．如图，△ABC的顶点A、B、C在边长为1的正方形网格的格点上，BD⊥AC于点D，则CD的长为（　　）

A． B． C． D．
10．如图所示的正方体中，Q，R，S是棱PB上的点，一只蚂蚁从A点出发，沿着正方体的侧面爬行，经过PB上一点，爬行到C点，若此蚂蚁所爬行的路线最短，那么P，Q，R，S四个点中，它最有可能经过的点是（　　）

A．P B．Q C．R D．S
二、填空题（每题3分，共21分）
11．比较大小：　 　．（填“＞”，“＜”或“＝”）
12．已知一个数的两个平方根分别是2x+1与3﹣x，那么这个数是　 　．
13．如果，那么2x﹣y的值为 　 　
14．若与互为相反数，那么的值为 　 　．
15．如图所示，已知四边形ABCD是边长为2的正方形，AP＝AC，则数轴上点P所表示的数是　 　．

16．如图，在Rt△ABC中，∠B＝90°，AB＝4，BC＝3，AC的垂直平分线交AB于点M，交AC于点N，则BM的长为 　 　．

17．如图，在Rt△ABC中，∠C＝90°，AB＝5cm，AC＝3cm，动点P从点B出发，沿射线BC以2cm/s的速度移动设运动的时间为ts当t＝　 　时，△ABP为直角三角形．

三、解答题.
18．化简与计算：
（1）；
（2）．
19．化简求值
已知y＝，求的值．
20．阅读材料：∵，∴的整数部分为的小数部分为．
解决问题：
（1）填空：的小数部分是 　 　；
（2）已知a是的整数部分，b是的小数部分，求代数式（a+1）3+（b+4）2的值．
21．如图，地面上放着一个小凳子，点A距离墙面40cm，在图①中，一根细长的木杆一端与墙角重合，木杆靠在点A处，OA＝50cm．在图②中，木杆的一端与点B重合，另一端靠在墙上点C处．

（1）求小凳子的高度；
（2）若OC＝90cm，木杆的长度比AB长60cm，求木杆的长度和小凳子坐板的宽AB．
22．把一张矩形纸片按如图方式折叠，使顶点B和点D重合，折痕为EF．若AB＝8cm，BC＝16cm．
（1）求重叠部分△DEF的面积；
（2）求折痕EF的长．

23．我们新定义一种三角形：两边平方和等于第三边平方的4倍的三角形叫做常态三角形，例如：某三角形三边长分别是5，6和8，因为62+82＝4×52＝100，所以这个三角形是常态三角形．
（1）若△ABC三边长分别是2，和4，则此三角形 　 　常态三角形（填“是”或“不是”）；
（2）若Rt△ABC是常态三角形，则此三角形的三边长之比为 　 　（请按从小到大排列）；
（3）如图，Rt△ABC中，∠ACB＝90°，BC＝6，点D为AB的中点且CD＝AB，连接CD，若△BCD是常态三角形，求△ABC的面积．



参考答案
一、选择题（每题3分，共30分）
1．在下列实数3.1415926，，，，，中无理数的个数有（　　）
A．2个 B．3个 C．4个 D．5个
【分析】无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．
解：在所列的6个数中，无理数有，这2个，
故选：A．
2．下面四组数，其中是勾股数的一组是（　　）
A．32，42，52 B．0.3，0.4，0.5
C．3，4，5 D．6，7，8
【分析】根据勾股数的定义：满足a2+b2＝c2 的三个正整数，称为勾股数解答即可．
解：A、（32）2+（42）2≠（52 ），不能构成勾股数，故错误；
B、0.32+0.42＝0.52，但是它们不是整数，所以能不是勾股数，故错误；
C、32+42＝52能构成勾股数，故正确；
D、62+72≠82不能构成勾股数，故错误；
故选：C．
3．的算术平方根为（　　）
A．9 B．±9 C．3 D．±3
【分析】直接根据算术平方根的定义进行解答即可．
解：∵＝9，32＝9
∴的算术平方根为3．
故选：C．
4．若﹣，且x是整数，则满足条件的x值有（　　）
A．5个 B．4个 C．3个 D．2个
【分析】先估算出、的大小，然后找出符合条件的数即可．
解：∵1＜3＜4＜5，
∴1＜．
∴﹣．
∴符合条件的x的值为：﹣2，﹣1，0，1．
故选：B．
5．满足下列条件的△ABC，不是直角三角形的是（　　）
A．b2＝c2﹣a2 B．a：b：c＝3：4：5
C．∠C＝∠A﹣∠B D．∠A：∠B：∠C＝12：13：15
【分析】掌握直角三角形的判定及勾股定理的逆定理是解题的关键．
解：A、由b2＝c2﹣a2得c2＝a2+b2符合勾股定理的逆定理，故是直角三角形；
B、由a：b：c＝3：4：5得c2＝a2+b2符合勾股定理的逆定理，故是直角三角形；
C、由三角形三个角度数和是180°及∠C＝∠A﹣∠B解得∠A＝90°，故是直角三角形；
D、由∠A：∠B：∠C＝12：13：15，及∠A+∠B+∠C＝180°得∠A＝54°，∠B＝58.5°，∠C＝67.5°，没有90°角，故不是直角三角形．
故选：D．
6．要使有意义，x的取值范围是（　　）
A．x≥2021 B．x≤2021 C．x＞2021 D．x＜2021
【分析】直接利用二次根式有意义被开方数是非负数，再结合分式有意义分母不等于零即可得出答案．
解：要使有意义，则2021﹣x＞0，
解得：x＜2021．
故选：D．
7．已知实数a在数轴上的对应点位置如图，则化简的结果是（　　）

A．2a﹣3 B．﹣1 C．1 D．3﹣2a
【分析】根据数轴上a点的位置，判断出（a﹣1）和（a﹣2）的符号，再根据非负数的性质进行化简．
解：由图知：1＜a＜2，
∴a﹣1＞0，a﹣2＜0，
原式＝a﹣1﹣[﹣（a﹣2）]＝a﹣1+（a﹣2）＝2a﹣3．
故选：A．
8．如图，一棵大树在离地面6m，10m两处折成三段，中间一段AB恰好与地面平行，大树顶部落在离大树底部12m处，则大树折断前的高度是（　　）

A．14m B．16m C．18m D．20m
【分析】作BO⊥DC于点O，首先由题意得：AD＝BO＝6m，AB＝OD＝4m，然后根据DC＝6米，得到OC＝8米，最后利用勾股定理得BC的长度即可．
解：如图，作BO⊥DC于点O，

由题意得：AD＝BO＝6m，AB＝OD＝4m，
∵DC＝12m，
∴OC＝8m，
∴由勾股定理得：BC＝（m），
∴大树的高度为10+10＝20（m），
故选：D．
9．如图，△ABC的顶点A、B、C在边长为1的正方形网格的格点上，BD⊥AC于点D，则CD的长为（　　）

A． B． C． D．
【分析】利用勾股定理求得相关线段的长度，然后由面积法求得BD的长度，再利用勾股定理即可求出CD的长．
解：如图，由勾股定理得 AC＝＝．
∵BC×2＝AC•BD，
即×2×2＝וBD，
∴BD＝，
∴CD＝＝，
故选：A．
10．如图所示的正方体中，Q，R，S是棱PB上的点，一只蚂蚁从A点出发，沿着正方体的侧面爬行，经过PB上一点，爬行到C点，若此蚂蚁所爬行的路线最短，那么P，Q，R，S四个点中，它最有可能经过的点是（　　）

A．P B．Q C．R D．S
【分析】根据立方体的展开图中从A点到C点最短路径共3种距离相同，进而画图得出答案．
解：如图所示：一只蚂蚁从A点出发，沿着正方体的侧面爬行，经过PB上一点，爬行到C点，若此蚂蚁所爬行的路线最短，那么P，Q，R，S四个点中，它最有可能经过的点是R点．
故选：C．

二、填空题（每题3分，共21分）
11．比较大小：　＜　．（填“＞”，“＜”或“＝”）
【分析】利用求差法进行比较即可．
解：﹣＝﹣＝，
∵（2）2＝20，52＝25，
∴2＜5，
∴2﹣5＜0，
∴＜0，
∴＜，
故答案为：＜．
12．已知一个数的两个平方根分别是2x+1与3﹣x，那么这个数是　49　．
【分析】根据一个数的平方根互为相反数，可得这个数的平方根，再根据互为相反数的和等于0，可得平方根，再根据平方，可得这个数．
解：∵一个数的两个平方根分别是2x+1与3﹣x，
∴（2x+1）+（3﹣x）＝0
x＝﹣4，
3﹣x＝3﹣（﹣4）＝7，
72＝49，
故答案为：49．
13．如果，那么2x﹣y的值为 　﹣8　
【分析】根据非负数的性质列出算式，求出x、y的值，计算即可．
解：∵，而，（2y﹣4）2≥0，
∴x+3＝0，2y﹣4＝0，
解得x＝﹣3，y＝2，
∴2x﹣y＝﹣6﹣2＝﹣8．
故答案为：﹣8．
14．若与互为相反数，那么的值为 　﹣1　．
【分析】这两个立方根互为相反数，那么被开方数互为相反数，和为0，求出x，再带入求值即可．
解：根据题意得：1﹣2x+3x﹣5＝0，
∴x＝4，
∴原式＝（1﹣2）2021
＝（﹣1）2021
＝﹣1，
故答案为：﹣1．
15．如图所示，已知四边形ABCD是边长为2的正方形，AP＝AC，则数轴上点P所表示的数是　1﹣2　．

【分析】根据勾股定理，可得AC的长，根据数轴上两点间的距离，可得答案．
解：AC＝＝2，
AP＝AC＝2，
1﹣2，
P点坐标1﹣2．
故答案为：1﹣2．
16．如图，在Rt△ABC中，∠B＝90°，AB＝4，BC＝3，AC的垂直平分线交AB于点M，交AC于点N，则BM的长为 　　．

【分析】连接CM，由MN是AC的垂直平分线，得AM＝CM，在△MBC中，设BM＝x，由勾股定理列出方程求解即可．
解：如图，连接CM，

设BM＝x，则AM＝4﹣x，
∵MN是AC的垂直平分线，
∴AM＝CM＝4﹣x，
在△MBC中，由勾股定理得：
BM2+BC2＝CM2，
即x2+32＝（4﹣x）2，
解得：x＝，
∴BM的长为，
故答案为：．
17．如图，在Rt△ABC中，∠C＝90°，AB＝5cm，AC＝3cm，动点P从点B出发，沿射线BC以2cm/s的速度移动设运动的时间为ts当t＝　2s或s　时，△ABP为直角三角形．

【分析】首先根据勾股定理求出BC的长度，再分两种情况：①当∠APB为直角时，②当∠BAP为直角时，分别求出此时的t值即可．
解：∵∠C＝90°，AB＝5cm，AC＝3cm，
∴BC＝4 cm．
①当∠APB为直角时，点P与点C重合，BP＝BC＝4 cm，
∴t＝4÷2＝2s．
②当∠BAP为直角时，BP＝2tcm，CP＝（2t﹣4）cm，AC＝3 cm，
在Rt△ACP中，AP2＝32+（2t﹣4）2，
在Rt△BAP中，AB2+AP2＝BP2，
∴52+[32+（2t﹣4）2]＝（2t）2，
解得t＝s．
综上，当t＝2s或s时，△ABP为直角三角形．
故答案为：2s或s．
三、解答题.
18．化简与计算：
（1）；
（2）．
【分析】（1）根据算术平方根，绝对值，立方根，幂的意义计算即可；
（2）根据二次根式的乘除法法则和平方差公式计算即可．
解：（1）原式＝3+3﹣﹣4﹣1
＝1﹣；

（2）原式＝+1﹣﹣[22﹣（）2]
＝2+1﹣2﹣（4﹣3）
＝1﹣1
＝0．
19．化简求值
已知y＝，求的值．
【分析】先利用二次根式有意义的条件确定x＝，y＝，再利用完全平方公式把展开合并，然后把x、y的值代入计算即可．
解：根据题意得1﹣4x≥0且4x﹣1≥0，
∴x＝，
∴y＝，
∴原式＝2x+2+y﹣（2x﹣2+y）
＝4
＝4
＝4×
＝2．
20．阅读材料：∵，∴的整数部分为的小数部分为．
解决问题：
（1）填空：的小数部分是 　﹣8　；
（2）已知a是的整数部分，b是的小数部分，求代数式（a+1）3+（b+4）2的值．
【分析】（1）估算出的范围，即可得出答案；
（2）故选出﹣3的范围，求出a，b的值，再代入求解即可．
解：（1）∵64＜73＜81，
∴8＜＜9，
∴的整数部分是8，小数部分是﹣8，
故答案为：﹣8；
（2）∵16＜19＜25，
∴4＜＜5，
∴1＜﹣3＜2，
∴a＝1，b＝﹣3﹣1＝﹣4，
∴原式＝23+（）2
＝8+19
＝27．
21．如图，地面上放着一个小凳子，点A距离墙面40cm，在图①中，一根细长的木杆一端与墙角重合，木杆靠在点A处，OA＝50cm．在图②中，木杆的一端与点B重合，另一端靠在墙上点C处．

（1）求小凳子的高度；
（2）若OC＝90cm，木杆的长度比AB长60cm，求木杆的长度和小凳子坐板的宽AB．
【分析】（1）过A作AM垂直于墙面，垂足M，根据勾股定理解答即可；
（2）延长BA交墙面于点N，根据勾股定理解答即可．
解：（1）过A作AM垂直于墙面，垂足M，

根据题意可得，AM＝40cm，
在Rt△AOM中，，
即凳子的高度为30cm．
（2）延长BA交墙面于点N，可得∠BNC＝90°，
设AB＝xcm，则CB＝x+60，BN＝x+40，CN＝90﹣30＝60，
在Rt△BCN中，BN2+CN2＝BC2（40+x）2+602＝（60+x）2x＝40BC＝60+40＝100（cm）．
22．把一张矩形纸片按如图方式折叠，使顶点B和点D重合，折痕为EF．若AB＝8cm，BC＝16cm．
（1）求重叠部分△DEF的面积；
（2）求折痕EF的长．

【分析】（1）由翻折的性质可知：AE＝A′E，AB＝A′D，∠A＝∠A′，然后在△A′ED中，利用勾股定理可求得DE的长，从而可求得△DEF的面积；
（2）过点E作EG⊥BC，在△DFC中，由勾股定理求得FC的长，从而可求得GF的长，最后在△EGF中利用勾股定理求得EF的长即可．
解：（1）由翻折的性质可知：AE＝A′E，AB＝A′D＝8，∠A＝∠A′＝90°．
设DE＝x，则A′E＝16﹣x．
在Rt△A′ED中，由勾股定理得：ED2＝A′E2+A′D2，即x2＝（16﹣x）2+82．
解得：x＝10．
∴DE＝10．
∴△DEF的面积＝＝＝40cm2．
（2）如图所示，过点E作EG⊥BC．

由翻折的性质可知：BF＝FD．
设CF＝y，则DF＝16﹣y
在Rt△CFD中，由勾股定理得：DF2＝FC2+DC2，即（16﹣y）2＝y2+82．
解得：y＝6．
∴GF＝GC﹣FC＝10﹣6＝4．
在Rt△EFG中，由勾股定理得：EF＝＝＝4．
23．我们新定义一种三角形：两边平方和等于第三边平方的4倍的三角形叫做常态三角形，例如：某三角形三边长分别是5，6和8，因为62+82＝4×52＝100，所以这个三角形是常态三角形．
（1）若△ABC三边长分别是2，和4，则此三角形 　是　常态三角形（填“是”或“不是”）；
（2）若Rt△ABC是常态三角形，则此三角形的三边长之比为 　：：　（请按从小到大排列）；
（3）如图，Rt△ABC中，∠ACB＝90°，BC＝6，点D为AB的中点且CD＝AB，连接CD，若△BCD是常态三角形，求△ABC的面积．

【分析】（1）由22+42＝4×＝20，符合定义；
（2）设两直角边长为：a、b，斜边长为c，则a2+b2＝c2，a2+c2＝4b2，可得a：b＝，从而得出答案；
（3）由△BCD是常态三角形，分CD2+BD2＝4×62或CD2+BC2＝4×BD2，可分别计算出CD的长，从而解决问题．
解：（1）∵22+42＝4×＝20，
∴△ABC是常态三角形，
故答案为：是；
（2）∵Rt△ABC是常态三角形，
∴设两直角边长为：a、b，斜边长为c，
则a2+b2＝c2，a2+c2＝4b2，
∴2a2＝3b2，
∴a：b＝，
设a＝，b＝x，
则c＝x，
∴此三角形的三边比为：：：，
故答案为：：：；
（3）在Rt△ABC中，∠ACB＝90°，BC＝6，点D为AB的中点，
∴当AD＝BD＝CD，
∵△BCD是常态三角形，
当CD2+BD2＝4×62时，
解得：BD＝CD＝6，
则AB＝12，
∴AC＝＝6，
∴△ABC的面积为：＝18，
当CD2+BC2＝4×BD2时，
解得：BD＝CD＝2，
则AB＝4，
∴AC＝2，
∴△ABC的面积为：＝6，
∴△ABC的面积为18或6．