一轮复习专题03 简单的逻辑联结词、全称量词与存在量词（解析版）教案

03简单的逻辑联结词、全称量词与存在量词

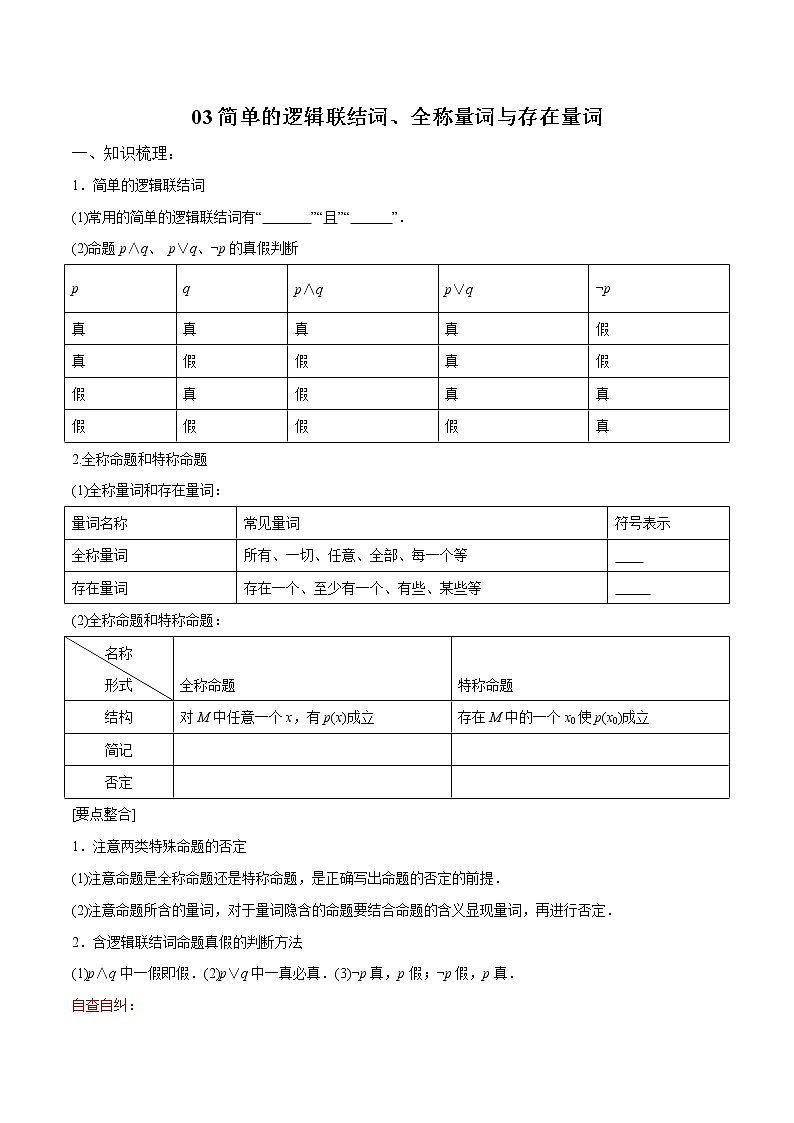
一、知识梳理：

1．简单的逻辑联结词

(1)常用的简单的逻辑联结词有“       ”“且”“      ”．

(2)命题p∧q、 p∨q、¬p的真假判断

2.全称命题和特称命题

(1)全称量词和存在量词：

(2)全称命题和特称命题：

[要点整合]

1．注意两类特殊命题的否定

(1)注意命题是全称命题还是特称命题，是正确写出命题的否定的前提．

(2)注意命题所含的量词，对于量词隐含的命题要结合命题的含义显现量词，再进行否定．

2．含逻辑联结词命题真假的判断方法

(1)p∧q中一假即假．(2)p∨q中一真必真．(3)¬p真，p假；¬p假，p真．

自查自纠：

1．(1)或  且  非

2.(1) ∀  ∃  (2) ∀x∈M，p(x)    ∃x0∈M，p(x0)   ∃x0∈M，¬p(x0)    ∀x∈M，¬p(x)

二、题型训练：

题组一

1．如果命题“且”是假命题，“”也是假命题，则（    ）

A．命题“或”是假命题B．命题“或”是假命题

C．命题“且”是真命题D．命题“且”是真命题

【答案】C

【解析】∵“且”是假命题，“”也是假命题，∴命题真，命题假，命题真，故选C．

2．若是真命题，是假命题，则（     ）

A．是真命题   B．是假命题C．是真命题    D．是真命题

【答案】D

【解析】试题分析：因为是真命题，是假命题，所以是假命题；是真命题  ；是假命题  ；是真命题，所以选D．

3． “是真命题”是“为假命题”的(    )

A．必要不充分条件   B．充分不必要条件   C．充分必要条件  D．既不充分也不必要条件

【答案】A．

【解析】①是真命题为真命题或为真命题，不能得出是假命题，即是真命题不能得出是假命题；②是假命题是真命题是真命题．由①②可知“是真命题”是“为假命题”的必要不充分条件，故选A．

4．若命题“”为假，且“”为假，则（    ）

A．或为假    B．假     C．真     D．不能判断的真假

【答案】B

【解析】“”为假，所以为假，命题“”为假，所以假.

5．在一次跳伞中，甲、乙两位学员各跳一次，设命题p是“甲降落在指定范围”，q是“乙降落在指定范围”，则命题“至少有一位学员没有降落在指定范围”可表示为(　　)

A．(p)∨(q)  B．p∨(q)  C．(p)∧(q)  D．p∨q

【答案】A

【解析】 “至少一位学员没降落在指定区域”即“甲没降落在指定区域或乙没降落在指定区域”，可知选A.

6．已知命题，，命题，，则（）

（A）命题是假命题                  （B）命题是真命题

（C）命题是真命题               （D）命题是假命题

【答案】C

【解析】：因为命题，是真命题，而命题，是假命题，由复合命题的真值表可知命题是真命题．故选C．

7．已知命题，命题，则（    ）

（A）命题是假命题             （B）命题是真命题

（C）命题是假命题               （D）命题是真命题

【答案】B

【解析】对命题，作出的图象可知其成立.对命题，由于 时，，所以命题是假命题，由此可知B正确.

8．设命题：“方程有两个实数根”；命题：“方程无实根”，若为假，为假，则实数的取值范围为               ．

【答案】

【解析】若方程有两个实根，则，

解得或 ， 即: 或 ；  4分

若方程无实根，则，

解得，  即．     8分

由于若为假，则，至少有一个为假；又为假，则真．所以为假，

即假真，从而有     解得 ．  11分

所以，实数的取值范围是．     12分

9．已知命题，使；命题，都有．给出下列结论：①题是真命题②命题是假命题③命题是真命题 ④命题是假命题其中正确的是（     ）

A．②④    B．②③    C．③④    D．①②③

【答案】B

【解析】：命题是假命题；命题是真命题；所以②、③正确，故选B．

题组二

10．命题“所有不能被2整除的整数都是奇数”的否定是(　　)

A．所有能被2整除的整数都是奇数

B．所有不能被2整除的整数都不是奇数

C．存在一个能被2整除的整数是奇数

D．存在一个不能被2整除的整数不是奇数

【答案】D

【解析】命题“所有不能被2整除的整数都是奇数”的否定是“存在一个不能被2整除的整数不是奇数”，选D.

11．命题“使得”的否定是 (   )

A．均有　　　　　B．均有

C．使得　　　　　D．均有

【答案】B

【解析】存在性命题的否定是全称命题. 命题“使得”的否定是均有，故选.

12．已知命题p：≤0，则(     )

A. p是假命题；p：≤0

B. p是假命题；p：＞0

C. p是真命题；p：≤0

D. p是真命题；p：＞0

【答案】B

【解析】∵3x>0，∴3x＋1>1，则log2(3x＋1)>0，∴p是假命题；：∀x∈R，log2(3x＋1)>0.

13．写出命题P：的否定．

【答案】

【解析】：特称命题的否定是全称命题，需将满足的条件加以否定的否定是

14．已知命题，则为．

【答案】

【解析】因为命题的否定为，因此为：

15．命题“，”的否定是（   ）

A．，         B．，

C．，           D．，

【答案】C

【解析】由特称命题的否定为全称命题可知，所求命题的否定为，，故应选．

16．命题：“存在，使得”的否定为（    ）

A、存在，使得B、存在，使得

C、对任意，都有D、对任意，都有

【答案】D

【解析】特称命题的否定是全称命题，并且需对结论加以否定，的否定为，因此存在，使得的否定为对任意，都有

17．命题“，使得”的否定是                       ．

【答案】

【解析】因为命题“”的否定是“”，所以命题“，使得”的否定是

题组三

18．已知命题,和命题,且为真，为假，则实数的取值范围为                     ．

【答案】．

【解析】由不等式<,， 即命题：， 所以命题：或，

又由，得，得命题：所以命题：或，

由题知：和必有一个为真一个为假．当真假时：当真假时：所以实数的范围是．

19．已知有两个不等的负数根，函数在上是增函数。若或为真，且为假，则实数的取值范围                      ．

【答案】或

【解析】有两个不等的负根

函数在上是增函数

（1）若真，假，则；

（2）若假，真，则

综上，得，或

20．命题；命题：解集非空．若假，假，则的取值范围为               ．

【答案】

【解析】不妨设为真，要使得不等式恒成立只需 ，

又∵当时，（当且仅当时取“=”）∴不妨设为真，要使得不等式有解只需，即解得或者∵假，且“”为假命题,  故 真假 所以 ∴实数的取值范围为