(广西版)中考数学总复习课件16《二次函数的图象和性质》(含答案)

这是一份(广西版)中考数学总复习课件16《二次函数的图象和性质》(含答案)，共36页。PPT课件主要包含了考点自查，对点自评，图16-1，答案B，2或≤2，图16-2，答案4，答案0，图16-3，图16-4等内容，欢迎下载使用。

二次函数的定义及解析式　 二次函数的图象和性质　二次函数解析式的确定及函数图象的平移　二次函数与方程的关系
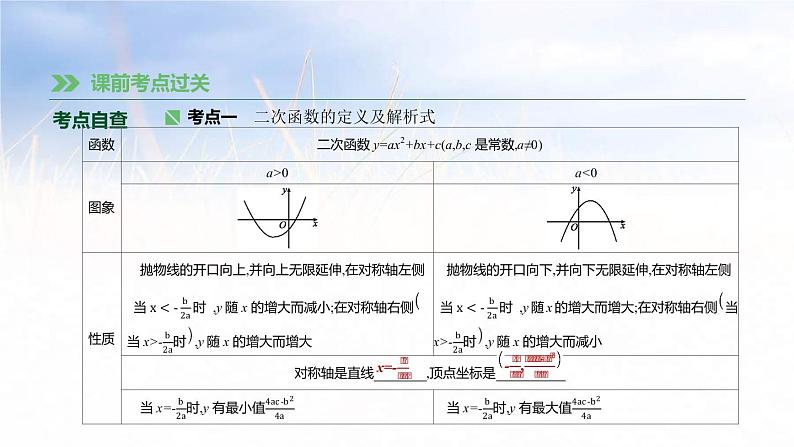
1.二次项系数a二次函数y=ax2+bx+c中,a作为二次项系数,显然a≠0.(1)当a>0时,抛物线的开口　　　　; (2)当a<0时,抛物线的开口　　　　　. 总结起来,a决定了抛物线开口的大小和方向,|a|越大,抛物线的开口越　　　　,|a|越小,抛物线的开口越　　　　. 
3.常数项c(1)当c>0时,抛物线与y轴的交点在y轴　　　　半轴上; (2)当c=0时,抛物线与y轴的交点为坐标原点;(3)当c<0时,抛物线与y轴的交点在y轴　　　　半轴上. 总结起来,c决定了抛物线与y轴交点的位置当b2-4ac>0时,抛物线与x轴有　　　　个交点; 当b2-4ac=0时,抛物线与x轴有　　　　个交点; 当b2-4ac<0时,抛物线与x轴有　　　　个交点. 总结起来,b2-4ac决定了抛物线与x轴的交点个数.
1.二次函数解析式的确定二次函数解析式的表达形式有:(1)一般式y=ax2+bx+c(a,b,c是常数,a≠0);(2)顶点式y=a(x-h)2+k,顶点为(h,k);(3)交点式y=a(x-x1)(x-x2),其中x1,x2表示图象与x轴的两交点,即(x1,0),(x2,0)的横坐标.强化理解:(1)若已知抛物线上三点的坐标,可设一般式求解;(2)若已知抛物线的顶点坐标或对称轴直线,则可采用顶点式y=a(x-h)2+k,其中顶点为(h,k),对称轴为直线x=h;(3)若已知抛物线与x轴的交点坐标或交点的横坐标,则可采用交点式y=a(x-x1)(x-x2),其中x1,x2表示图象与x轴的两交点,即(x1,0),(x2,0)的横坐标.
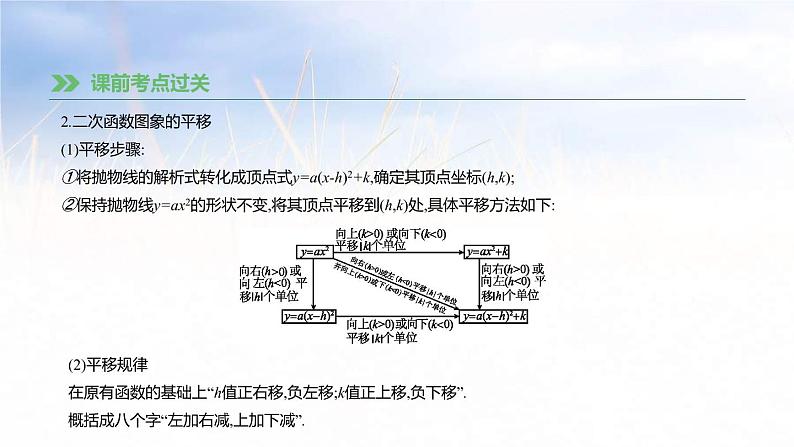
2.二次函数图象的平移(1)平移步骤:①将抛物线的解析式转化成顶点式y=a(x-h)2+k,确定其顶点坐标(h,k);②保持抛物线y=ax2的形状不变,将其顶点平移到(h,k)处,具体平移方法如下:
(2)平移规律在原有函数的基础上“h值正右移,负左移;k值正上移,负下移”.概括成八个字“左加右减,上加下减”.
二次函数y=ax2+bx+c,等号左边是函数y,右边是关于自变量x的二次三项式,当函数值y=0时,x的取值就是一元二次方程ax2+bx+c=0(a≠0)的解,即y=ax2+bx+c的图象与x轴的交点的横坐标就是一元二次方程ax2+bx+c=0(a≠0)的解.下面以a>0时为例,揭示二次函数和一元二次方程之间的内在联系:
1.对于二次函数y=-(x-1)2+2的图象与性质,下列说法正确的是(　　)A.对称轴是直线x=1,最小值是2B.对称轴是直线x=1,最大值是2C.对称轴是直线x=-1,最小值是2D.对称轴是直线x=-1,最大值是2
2.抛物线y=x2向右平移2个单位,再向上平移3个单位后,所得新抛物线的解析式为(　　)A.y=(x+2)2+3B.y=(x-2)2+3C.y=(x+2)2-3D.y=(x-2)2-3
3.若抛物线y=(x-m)2+m+1的顶点在第一象限,则m的取值范围为(　　)A.m>1B.m>0C.m>-1D.-14.在平面直角坐标系xOy中,二次函数y=ax2+bx+c的图象如图16-1所示.下列说法正确的是(　　)A.abc<0,b2-4ac>0B.abc>0,b2-4ac>0C.abc<0,b2-4ac<0D.abc>0,b2-4ac<0
5.已知二次函数y=(x-2)2+3,当x　　　 　时,y随x的增大而减小. 
7.如图16-2,直线y=mx+n与抛物线y=ax2+bx+c交于A(-1,p),B(4,q)两点,则关于x的不等式mx+n>ax2+bx+c的解集是　　　　. 
6.若二次函数y=x2-4x+n的图象与x轴只有一个公共点,则实数n=　　　　. 
[解析] 二次函数y=x2-4x+n的图象与x轴只有一个公共点,说明“Δ=b2-4ac=0”,即(-4)2-4×1×n=0.所以n=4.
[答案] x<-1或x>4
[解析] 由函数图象可知,在点A的左侧和点B的右侧,一次函数的函数值都大于二次函数的函数值.∵A(-1,p),B(4,q),∴关于x的不等式mx+n>ax2+bx+c的解集是x<-1或x>4.
8.抛物线y=ax2+bx+c经过点A(-3,0),对称轴是直线x=-1,则a+b+c=　　　　. 
[解析] 点A(-3,0)关于直线x=-1的对称点是点(1,0),故当x=1时,a+b+c=0.
【失分点】　　二次函数图象的顶点坐标公式中横坐标的符号选取记忆混乱;二次函数求最值忽视自变量取值范围对结果的影响.
9.将二次函数y=x2-2x+3化为y=(x-h)2+k的形式,则h=　　　　,k=　　　　. 
10.在-2≤x≤4这个范围内,二次函数y=x2的最大值是　　　　,最小值是　　　　. 
解: (2)当x=-1时,y有最小值-3.
解: (3)∵抛物线开口向上,对称轴为直线x=-1,∴当x<-1时,y随x的增大而减小.
拓展1 [2018·成都] 关于二次函数y=2x2+4x-1,下列说法正确的是(　　)A.图象与y轴的交点坐标为(0,1)B.图象的对称轴在y轴的右侧C.当x<0时,y的值随x值的增大而减小D.y的最小值为-3
拓展2 点P1(-1,y1),P2(3,y2),P3(5,y3)均在二次函数y=-x2+2x+c的图象上,则y1,y2,y3的大小关系是(　　)A.y3>y2>y1B.y3>y1= y2C.y1>y2>y3D.y1=y2>y3
拓展4 已知函数y=ax2-2ax-1(a是常数,a≠0),下列结论正确的是(　　)A.当a=1时,函数图象经过点(-1,0)B.当a=-2时,函数图象与x轴没有交点C.若a<0,函数图象的顶点始终在x轴的下方D.若a>0,则当x≥1时,y随x的增大而增大
[解析] A.当a=1时,函数解析式为y=x2-2x-1,当x=-1时,y=1+2-1=2,∴当a=1时,函数图象经过点(-1,2),∴A选项不符合题意;B.当a=-2时,函数解析式为y=-2x2+4x-1,令y=-2x2+4x-1=0,则Δ=42-4×(-2)×(-1)=8>0,∴当a=-2时,函数图象与x轴有两个不同的交点,∴B选项不符合题意;C.∵y=ax2-2ax-1=a(x-1)2-1-a,∴二次函数图象的顶点坐标为(1,-1-a),当-1-a<0时,有a>-1,∴C选项不符合题意;D.∵y=ax2-2ax-1=a(x-1)2-1-a,∴二次函数图象的对称轴为直线x=1.若a>0,则当x≥1时,y随x的增大而增大,∴D选项符合题意.故选D.
【方法模型】 (1)当已知抛物线上三点坐标求二次函数的解析式时,一般采用一般式y=ax2+bx+c.(2)当已知抛物线的顶点坐标(或对称轴或最大、最小值)求二次函数的解析式时,一般采用顶点式y=a(x-h)2+k.(3)当已知抛物线与x轴的交点坐标求二次函数的解析式时,一般采用交点式y=a(x-x1)(x-x2).
解: (2)由顶点A(-1,4),可设二次函数关系式为y=a(x+1)2+4(a≠0).∵二次函数的图象过点B(2,-5),∴-5=a(2+1)2+4,解得a=-1.∴二次函数的关系式是y=-(x+1)2+4.
解: (3)方法一:设抛物线的解析式为y=a(x+1)(x-3),把C(0,-3)代入得a×1×(-3)=-3,解得a=1,所以这个二次函数的解析式为y=(x+1)(x-3)=x2-2x-3.
拓展 如图16-5,抛物线y=x2+bx+c经过坐标原点,并与x轴交于点A(2,0).(1)求此抛物线的解析式;(2)写出顶点坐标及对称轴;(3)若抛物线上有一点B,且S△OAB=3,求点B的坐标.
解：(2)∵y=x2-2x=(x-1)2-1,∴顶点坐标为(1,-1),对称轴为直线x=1.
例3 [2018·哈尔滨] 将抛物线y=-5x2+1向左平移1个单位长度,再向下平移2个单位长度,所得到的抛物线为(　　)A.y=-5(x+1)2-1B.y=-5(x-1)2-1C.y=-5(x+1)2+3D.y=-5(x-1)2+3
[解析] 给的抛物线解析式可以看作顶点式,顶点为(0,1),平移可以看作是顶点移动到(-1,-1),所以选A.
拓展2 [2016·柳州] 将抛物线y=2x2向上平移1个单位后所得抛物线的解析式为　　　　　　　. 
例4 已知y=ax2+bx+c的图象如图16-6,则:a　　　　0,b　　　　0,c　　　　0,a+b+c　　　　0,a-b+c　　　　0,b2-4ac　　　0.(用“>”或“<”填空) 
拓展 如图16-7所示,抛物线y=ax2+bx+c的顶点为B(-1,3),与x轴的交点A在点(-3,0)和(-2,0)之间,有以下结论:①b2-4ac=0;②a+b+c>0;③2a-b=0;④c-a=3.其中正确的有(　　)A.1个B.2个C.3个D.4个
例5 若二次函数y=ax2-2ax+c的图象经过点(-1,0),则方程ax2-2ax+c=0的解为(　　)A.x1=-3,x2=-1B.x1=1,x2=3C.x1=-1,x2=3D.x1=-3,x2=1
[解析] ∵二次函数y=ax2-2ax+c的图象经过点(-1,0),∴方程ax2-2ax+c=0一定有一个解为x=-1.∵抛物线的对称轴为直线x=1,∴二次函数y=ax2-2ax+c的图象与x轴的另一个交点为(3,0).∴方程ax2-2ax+c=0的解为x1=-1,x2=3.故选C.
拓展1 [2015·柳州] 如图16-8,二次函数y=ax2+bx+c的图象与x轴相交于(-2,0)和(4,0)两点,当函数值y>0时,自变量x的取值范围是(　　)A.x<-2B.-20 D.x>4
拓展2 [2014·柳州] 小兰画了一个函数y=x2+ax+b的图象如图16-9,则关于x的方程x2+ax+b=0的解是(　　)A.无解B.x=1C.x=-4D.x=-1或x=4
[解析] ∵函数y=x2+ax+b的图象与x轴交点的坐标分别是(-1,0),(4,0),∴关于x的方程x2+ax+b=0的解是x=-1或x=4.故选D.
拓展3 若二次函数y=x2+mx图象的对称轴是直线x=3,则关于x的方程x2+mx=7的解为(　　)A.x1=1,x2=-7B.x1=-1,x2=-7C.x1=1,x2=7D.x1=-1,x2=7
【方法点析】本题的已知条件简洁,结论明了,似乎没有什么可挖掘或拓广的,其实此题目乃平中见奇,内涵丰富,不但解法多样,而且数形结合思想、函数与方程思想贯穿其中,若要画图,还需分情况讨论.适当改变条件,可得出许多新颖的题目.
教材母题——人教版九上P47习题T4抛物线y=ax2+bx+c与x轴的公共点是(-1,0),(3,0),求这条抛物线的对称轴.
解：方法二:∵抛物线y=ax2+bx+c与x轴的两交点坐标是(-1,0),(3,0),∴抛物线的解析式可设为y=a(x+1)·(x-3)(a≠0),即y=a(x2-2x-3)=a(x-1)2-4a(a≠0).∴抛物线的对称轴为直线x=1.
解：方法三:∵抛物线是关于对称轴对称的,且其对称轴与x轴垂直,∴对称轴必过点(-1,0),(3,0)的中点.∴抛物线的对称轴为直线x=1.
拓展 [2017·南京] 已知函数y=-x2+(m-1)x+m(m为常数).(1)该函数的图象与x轴公共点的个数是(　　)A.0B.1C.2D.1或2(2)求证:不论m为何值,该函数图象的顶点都在函数y=(x+1)2的图象上.(3)当-2≤m≤3时,求该函数图象的顶点纵坐标的取值范围.
【思路提示】当y=0时,-x2+(m-1)x+m=0,则b2-4ac=(m-1)2+4m=(m+1)2≥0,所以一元二次方程有两个相等或两个不相等的实数根,即对应的二次函数图象与x轴有1个或2个交点.