备战2022 中考数学 人教版 一轮复习第二十二讲 圆的有关计算 专题练

这是一份备战2022 中考数学 人教版 一轮复习第二十二讲 圆的有关计算 专题练，文件包含备战2022中考数学人教版第二十二讲圆的有关计算专题练学生版doc、备战2022中考数学人教版第二十二讲圆的有关计算专题练教师版doc等2份试卷配套教学资源，其中试卷共28页， 欢迎下载使用。
第二十二讲　圆的有关计算


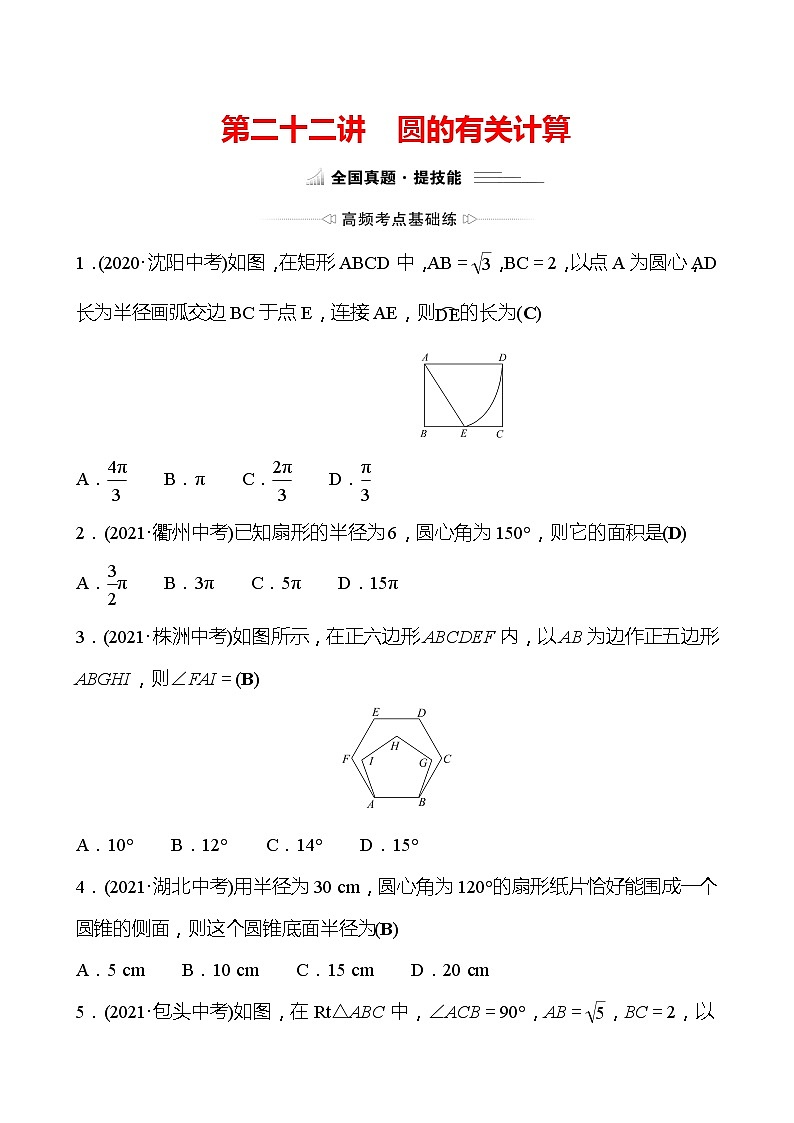
1．(2020·沈阳中考)如图，在矩形ABCD中，AB＝，BC＝2，以点A为圆心，AD长为半径画弧交边BC于点E，连接AE，则的长为(C)
　　　　　　　　　　　　　　　　　　
A． B．π C． D．
2．(2021·衢州中考)已知扇形的半径为6，圆心角为150°，则它的面积是(D)
A．π B．3π C．5π D．15π
3．(2021·株洲中考)如图所示，在正六边形ABCDEF内，以AB为边作正五边形ABGHI，则∠FAI＝(B)

A．10° B．12° C．14° D．15°
4．(2021·湖北中考)用半径为30 cm，圆心角为120°的扇形纸片恰好能围成一个圆锥的侧面，则这个圆锥底面半径为(B)
A．5 cm B．10 cm C．15 cm D．20 cm
5．(2021·包头中考)如图，在Rt△ABC中，∠ACB＝90°，AB＝，BC＝2，以点A为圆心，AC的长为半径画弧，交AB于点D，交AC于点C，以点B为圆心，AC的长为半径画弧，交AB于点E，交BC于点F，则图中阴影部分的面积为(D)

A．8－π　　B．4－π　　C．2－　　D．1－
6．(2021·青海中考)如图，一根5 m长的绳子，一端拴在围墙墙角的柱子上，另一端拴着一只小羊A，(羊只能在草地上活动)那么小羊A在草地上的最大活动区域面积是(B)

A．π m2　B．π m2　C．π m2　D．π m2
7．(2021·山西中考)如图，正六边形ABCDEF的边长为2，以A为圆心，AC的长为半径画弧，得，连接AC，AE，则图中阴影部分的面积为(A)

A．2π B．4π C．π D．π
8．(2021·聊城中考)用一块弧长16π cm的扇形铁片，做一个高为6 cm的圆锥形工件侧面(接缝忽略不计)，那么这个扇形铁片的面积为__80π__cm2.
9．(2021·绥化中考)边长为4 cm的正六边形，它的外接圆与内切圆半径的比值是____．
10．(2021·河南中考)如图所示的网格中，每个小正方形的边长均为1，点A，B，D均在小正方形的顶点上，且点B，C在上，∠BAC＝22.5°，则的长为____．

11．(2021·凉山州中考)如图，将△ABC绕点C顺时针旋转120°得到△A′B′C，已知AC＝3，BC＝2，则线段AB扫过的图形(阴影部分)的面积为____．

12．(2021·河北中考)如图，⊙O的半径为6，将该圆周12等分后得到表盘模型，其中整钟点为An(n为1～12的整数)，过点A7作⊙O的切线交A1A11延长线于点P.

(1)通过计算比较直径和劣弧长度哪个更长；
(2)连接A7A11，则A7A11和PA1有什么特殊位置关系？请简要说明理由；
(3)求切线长PA7的值．
【解析】(1)由题意，∠A7OA11＝120°，
∴的长＝＝4π＞12，
∴比直径长．
(2)结论：PA1⊥A7A11.
理由：连接A1A7，A7A11，OA11.
∵A1A7是⊙O的直径，
∴∠A7A11A1＝90°，
∴PA1⊥A7A11.
(3)∵PA7是⊙O的切线，
∴PA7⊥A1A7，
∴∠PA7A1＝90°，
∵∠PA1A7＝60°，A1A7＝12，
∴PA7＝A1A7·tan 60°＝12.


13．(2021·河北中考)如图，点O为正六边形ABCDEF对角线FD上一点，S△AFO＝8，S△CDO＝2，则S正六边形ABCDEF的值是(B)

A．20　　　　　　 B．30
C．40 D．随点O位置而变化
14．(2021·连云港中考)如图，正方形ABCD内接于⊙O，线段MN在对角线BD上运动，若⊙O的面积为2π，MN＝1，则△AMN周长的最小值是(B)

A．3　　　　B．4　　　　C．5　　　　D．6
15．(2021·玉林中考)如图，在正六边形ABCDEF中，连接对角线AD，AE，AC，DF，DB，AC与BD交于点M，AE与DF交于点为N，MN与AD交于点O，分别延长AB，DC于点G，设AB＝3.有以下结论：
①MN⊥AD；
②MN＝2；
③△DAG的重心、内心及外心均是点M；
④四边形FACD绕点O逆时针旋转30°与四边形ABDE重合，
则所有正确结论的序号是__①②③__．

16.(2021·通辽中考)如图，AB是⊙O的弦，AB＝2，点C是⊙O上的一个动点，且∠ACB＝60°，若点M，N分别是AB，BC的中点，则图中阴影部分面积的最大值是__－__．

17.(2021·黄石中考)如图，PA，PB是⊙O的切线，A，B是切点，AC是⊙O的直径，连接OP，交⊙O于点D，交AB于点E.

(1)求证：BC∥OP；
(2)若E恰好是OD的中点，且四边形OAPB的面积是16，求阴影部分的面积；
(3)若sin ∠BAC＝，且AD＝2，求切线PA的长．
【解析】(1)∵PA，PB是⊙O的切线，
∴PA＝PB，∵OA＝OB，∴OP⊥AB，
∵AC是直径，∴∠ABC＝90°，∴BC⊥AB，
∴BC∥OP.
(2)∵OE＝DE，AB⊥OD，∴OA＝AD，
∵OA＝OD，∴AD＝OA＝OD，
∴△AOD是等边三角形，∴∠AOD＝60°，
设OE＝m，则AE＝BE＝m，OA＝2m，OP＝4m，
∵四边形OAPB的面积是16，
∴·OP·AB＝16，
∴×4m×2m＝16，∴m＝2或－2(舍弃)，
∴OE＝2，AB＝4，OA＝2m＝4，
∵OD⊥AB，∴＝，
∴∠AOD＝∠BOD＝60°，
∴∠AOB＝2∠AOD＝120°，
∴S阴＝S扇形AOB－S△AOB
＝－×4×2＝－4.
(3)在Rt△AOE中，sin ∠BAC＝＝，
∴可以假设OE＝x，则OA＝OD＝3x，DE＝2x，
AE＝＝＝2x，
在Rt△ADE中，AD2＝AE2＋DE2，
∴(2)2＝(2x)2＋(2x)2，
∴x＝1或－1(舍弃)，
∴OE＝1，OA＝3，AE＝2，∵PA是切线，
∴PA⊥OA，∴∠OAP＝90°，
∴∠CAB＋∠PAB＝90°，∠APO＋∠PAE＝90°，
∴∠CAB＝∠APO，
∴sin ∠APE＝sin ∠CAB＝＝，
∴PA＝3AE＝6.

18.(2021·自贡中考)如图，直线y＝－2x＋2与坐标轴交于A，B两点，点P是线段AB上的一个动点，过点P作y轴的平行线交直线y＝－x＋3于点Q，△OPQ绕点O顺时针旋转45°，边PQ扫过区域(阴影部分)面积的最大值是(A)

A．π B．π C．π D．π

1．(2021·温州模拟)若扇形的弧长是5π，半径是18，则该扇形的圆心角是(A)
A．50° B．60° C．100° D．120°
2．(2021·苏州模拟)一个扇形的圆心角为120°，扇形的弧长等于4π，则该扇形的面积等于(C)
A．2π B．π C．12π D．24π
3．(2021·曲靖模拟)如图，四边形ABCD是⊙O的内接四边形，⊙O的半径为4，∠C＝120°，则优弧BD的长是(A)

A．π B．π C．π D．π
4．(2021·宁波模拟)如图，将扇形OAB沿弦BC向下折叠，∠AOB＝150°，OA＝2，则图中阴影部分的周长为(A)

A．＋4 B．＋4 C．＋2 D．＋2
5．(2021·沧州模拟)刘徽是我国魏晋时期卓越的数学家，他在《九章算术》中提出了“割圆术”，利用圆的内接正多边形逐步逼近圆来近似计算圆的面积．如图，若用圆的内接正十二边形的面积S1来近似估计⊙O的面积S，设⊙O的半径为1，则S－S1的值为(π≈3.14)(B)

A．0 B．0.14 C．0.5 D．1
6．(2021·南充模拟)如图所示，在边长为的正方形铁皮上剪下一个扇形和一个圆，使之恰好围成一个圆锥，则圆锥的高为(B)

A． B． C． D．
7．(2021·平顶山模拟)如图，点O为Rt△ABC的斜边AB的中点，∠C＝90°，
∠A＝30°，以点O为旋转中心顺时针旋转△ABC得到△A1B1C1，若BC＝2，当BC∥A1C1时，图中弧BC1所构成的阴影部分面积为(A)

A．－ B．＋
C．－ D．＋
8．(2021·扬州模拟)如图，正六边形ABCDEF的边长为5 cm，CF是对角线，则CF是__10__cm.

9．(2021·宁波模拟)如图，一个空间几何体的主视图和左视图都是边长为2的正三角形，俯视图是一个圆，那么这个几何体的侧面积是__2π__．

10．(2020·茂名模拟)如图，在⊙O中，半径OA⊥OB，过OA的中点C作FD∥OB交⊙O于D、F两点，且CD＝，以O为圆心，OC为半径作，交OB于E点，阴影部分的面积为__＋__．

11．(2021·昆明模拟)如图，点A1的坐标为(2，0)，过点A1作x轴的垂线交直线l：y＝x于点B1，以原点O为圆心，OB1的长为半径画弧交x轴正半轴于点A2；再过点A2作x轴的垂线交直线l于点B2，以原点O为圆心，OB2的长为半径画弧交x轴正半轴于点A3，…，按此作法进行下去，则的长是____．

12．(2021·武汉模拟)如图，C是半圆上一点，AB是直径，将弧BC沿BC翻折交AB于点D，再将弧BD沿BD翻折交BC于点E，若E是弧BD的中点，AD＝2，则阴影部分面积为__3＋2__．

13．(2021·宁波模拟)如图，在7×7的正方形网格(每个小正方形的边长为1)中，一条圆弧经过A，B，C三点．

(1)在正方形网格中直接标出这条圆弧所在圆的圆心O；
(2)求弧AC的长．
【解析】(1)如图，连接AB，BC作线段AB、线段BC的垂直平分线，两线交于点O，
则点O即为所求；

(2)连接AC，AO，OC，
∵AC2＝62＋22＝40，OA2＋OC2＝42＋22＋42＋22＝40，
∴AC2＝OA2＋OC2，
∴∠AOC＝90°，
在Rt△AOC中，∵OA＝OC＝2，
∴的长＝＝π.
14．(2021·湖州模拟)如图，BM是⊙O的直径，四边形ABMN是矩形，D是⊙O上的点，DC⊥AN，与AN交于点C，已知AC＝15，⊙O的半径为30.

(1)求的长．
(2)连接OD，若将扇形BOD卷成一个圆锥，求这个圆锥底面半径的长．
【解析】(1)连接OD，延长DC交BM于点E，

∵BM是⊙O的直径，四边形ABMN是矩形，D是⊙O上一点，DC⊥AN，
∴DE⊥BO，
∵AC＝15 cm，
∴BE＝15 cm，
∴EO＝15 cm，
∵DO＝30 cm，∴cos ∠DOE＝＝，
∴∠EOD＝60°，
∴的长＝＝10π(cm)；
(2)设圆锥底面半径为r cm，
则2πr＝10π，
解得r＝5，即圆锥底面半径的长为5 cm.
15．(2021·贵阳模拟)如图，在菱形ABCD中，对角线AC，BD交于点O，∠BAO＝30°，AC＝8.过点O作OH⊥AB于点H，以点O为圆心，OH为半径的半圆交AC于点M.

(1)求图中阴影部分的面积；
(2)点P是BD上的一个动点(点P不与点B，D重合)，当PH＋PM的值最小时，求PD的长度．
【解析】(1)∵四边形ABCD是菱形，

∴AC⊥BD，OA＝OC＝4，
∵OH⊥AB，∴∠AHO＝90°，
∵∠OAH＝30°，
∴∠AOH＝60°，OH＝OA＝2，AH＝OH＝2，
∴S阴＝S△AOH－S扇形OMH＝×2×2－＝2－π.
(2)作点M关于BD的对称点M′，连接HM′交BD于P，连接PM，此时PH＋PM的值最小．
∵OH＝OM′，∴∠OHM′＝∠OM′H，
∵∠AOH＝∠OHM′＋∠OM′H＝60°，
∴OP＝OM′·tan 30°＝，
∵OD＝OA·tan 30°＝，
∴PD＝OD＋OP＝＋＝2.
16．(2021·青岛模拟)[提出问题]正多边形内任意一点到各边距离之和与这个正多边形的边及内角有什么关系？

[探索发现](1)为了解决这个问题，我们不妨从最简单的正多边形正三角形入手
如图①，△ABC是正三角形，边长是a，P是△ABC内任意一点，P到△ABC各边距离分别为h1、h2、h3，确定h1＋h2＋h3的值与△ABC的边及内角的关系．
(2)如图②，五边形ABCDE是正五边形，边长是a，P是正五边形ABCDE内任意一点，P到五边形ABCDE各边距离分别为h1，h2，h3，h4，h5，参照(1)的探索过程，确定h1＋h2＋h3＋h4＋h5的值与正五边形ABCDE的边及内角的关系．
(3)类比上述探索过程：
正六边形(边长为a)内任意一点P到各边距离之和h1＋h2＋h3＋h4＋h5＋h6＝________．
正八边形(边长为a)内任意一点P到各边距离之和h1＋h2＋h3＋h4＋h5＋h6＋h7＋h8＝________．
[问题解决]正n边形(边长为a)内任意一点P到各边距离之和h1＋h2＋…＋hn＝________．
【解析】(1)设△ABC的面积为S，
显然S＝a(h1＋h2＋h3)，
设△ABC的中心(正多边形各边垂直平分线的交点，又称正多边形的中心)为O，
连接OA、OB、OC，
它们将△ABC分成三个全等的等腰三角形，
过点O作OM⊥AB，垂足为M，
易知OM＝AM tan ∠OAB＝AB tan ∠BAC＝a tan 30°，
所以S＝3S△OAB＝3×AB×OM＝3×a×a tan 30°＝a2tan 30°，
那么a(h1＋h2＋h3)＝a2tan 30°，
所以h1＋h2＋h3＝a tan 30°；
(2)设正五边形ABCDE的面积为S，
显然S＝a(h1＋h2＋h3＋h4＋h5)，
设正五边形ABCDE的中心为O，
连接OA、OB、OC、OD、OE，
它们将正五边形ABCDE分成五个全等的等腰三角形，过点O作OF⊥AB，垂足为F，
易知OF＝AF tan ∠OAB＝AB tan ∠BAE＝a tan 54°，
所以S＝5S△OAB＝5×AB×OF＝5×a×a tan 54°＝a2tan 54°，
那么a(h1＋h2＋h3＋h4＋h5)＝a2tan 54°，
所以h1＋h2＋h3＋h4＋h5＝a tan 54°.

(3)同理可证：
正六边形(边长为a)内任意一点P到各边距离之和h1＋h2＋h3＋h4＋h5＋h6＝3a tan 60°.
正八边形(边长为a)内任意一点P到各边距离之和h1＋h2＋h3＋h4＋h5＋h6＋h7＋h8＝4a tan 67.5°.
[问题解决]正n边形(边长为a)内任意一点P到各边距离之和h1＋h2＋…＋hn＝a tan °.
答案：3a tan 60°　4a tan 67.5°　a tan °.