中考数学一轮复习《圆的有关计算》知识要点及专题练习

这是一份中考数学一轮复习《圆的有关计算》知识要点及专题练习，共19页。试卷主要包含了知识要点，课标要求，常见考点，专题训练等内容，欢迎下载使用。

中考数学一轮复习知识点课标要求专题训练：圆的有关计算（含答案）
一、知识要点：
正多边形和圆
定义：正多边形的外接圆的圆心叫做这个正多边形的中心，外接圆的半径叫做正多边形的半径，正多边形每一边所对的圆心角叫做正多边形的中心角，中心正多边形的一边的距离叫做正多边形的边心距。
弧长和扇形面积
n°的圆心角所对的弧长l为：。
圆心角为n°的扇形面积S为：。
圆锥的侧面积为：S=πrl。圆锥的全面积为：S=πrl+πr2。
二、课标要求：
1、会计算圆的弧长、扇形的面积。
2、了解正多边形的概念及正多边形与圆的关系。
三、常见考点：
1、弧长和扇形面积，圆锥、圆柱的侧面积及其全面积
2、圆与其它知识(三角形、四边形、函数、相似)的综合运用。
四、专题训练：
1．如图，两个正六边形ABCDEF、EDGHIJ的顶点A、B、H、I在同一个圆上，点P在上，则tan∠API的值是（　　）

A．2 B．2 C．2 D．1
2．半径为3的正六边形的周长为（　　）
A．18 B． C． D．
3．在半径为6cm的圆中，60°的圆心角所对弧的弧长是（　　）
A．πcm B．2πcm C．3πcm D．6πcm
4．如图，已知⊙O的半径为3，弦AB⊥直径CD，∠A＝30°，则的长为（　　）

A．π B．2π C．3π D．6π
5．如图，在Rt△ABC中，∠C＝90°，∠B＝30°，AC＝1，以A为圆心AC为半径画圆，交AB于点D，则阴影部分面积是（　　）

A． B． C． D．
6．如图，AB是⊙的直径，半径OA的垂直平分线交⊙O于C，D两点，∠C＝30°，CD＝2，则阴影部分的面积是（　　）

A． B．π C． D．2π
7．如图，边长为2的正方形ABCD的中心与半径为3的⊙O的圆心重合，延长AB，BC分别交⊙O于M，N，则图中阴影部分的面积是（　　）

A． B． C．9π﹣4 D．9π﹣2
8．已知圆锥的底面半径为6cm，母线长为10cm，则这个圆锥的全面积是（　　）
A．60πcm2 B．96πcm2 C．132πcm2 D．168πcm2
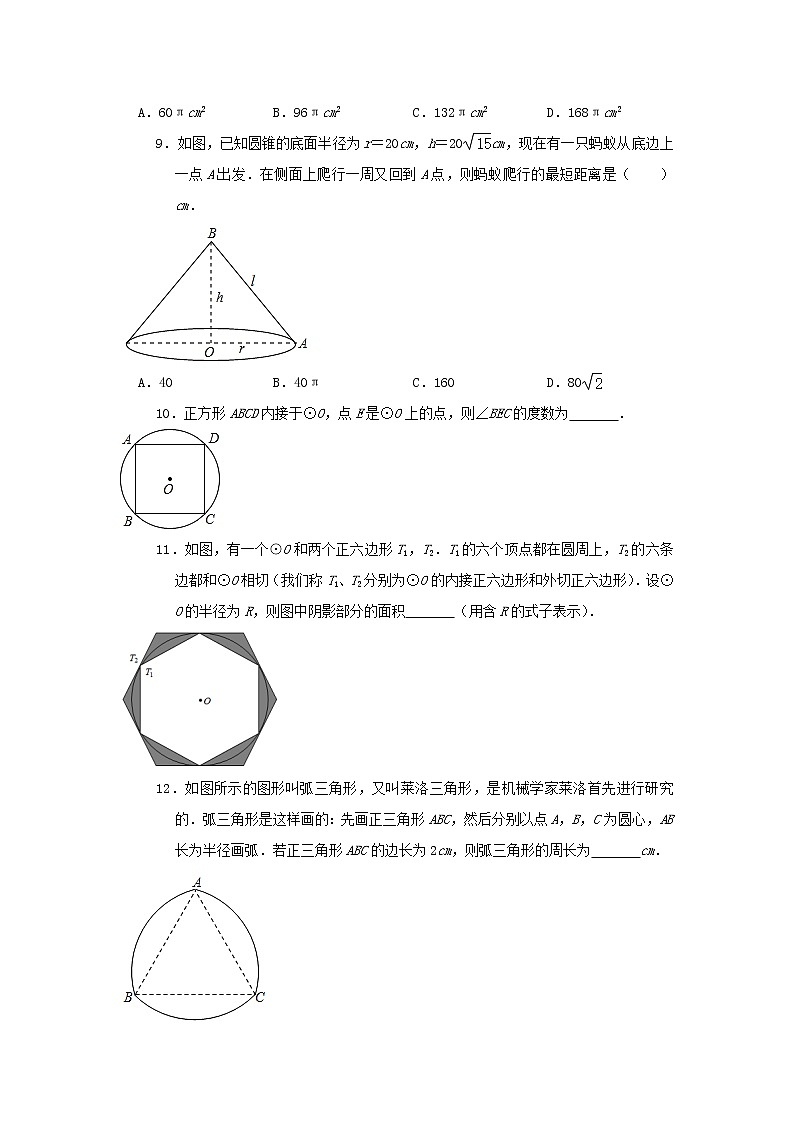
9．如图，已知圆锥的底面半径为r＝20cm，h＝20cm，现在有一只蚂蚁从底边上一点A出发．在侧面上爬行一周又回到A点，则蚂蚁爬行的最短距离是（　　）cm．

A．40 B．40π C．160 D．80
10．正方形ABCD内接于⊙O，点E是⊙O上的点，则∠BEC的度数为　 　．

11．如图，有一个⊙O和两个正六边形T1，T2．T1的六个顶点都在圆周上，T2的六条边都和⊙O相切（我们称T1、T2分别为⊙O的内接正六边形和外切正六边形）．设⊙O的半径为R，则图中阴影部分的面积　 　（用含R的式子表示）．

12．如图所示的图形叫弧三角形，又叫莱洛三角形，是机械学家莱洛首先进行研究的．弧三角形是这样画的：先画正三角形ABC，然后分别以点A，B，C为圆心，AB长为半径画弧．若正三角形ABC的边长为2cm，则弧三角形的周长为　 　cm．

13．如图，在平面直角坐标系中，四边形ABOC是正方形，点A的坐标为（1，1），弧AA1是以点B为圆心，BA为半径的圆弧；弧A1A2是以点O为圆心，OA2为半径的圆弧；弧A2A3是以点C为圆心，CA2为半径的圆弧；弧A3A4是以点A为圆心，AA3为半径的圆弧，继续以点B，O，C，A为圆心，按上述作法得到的曲线AA1A2A3A4A5…，称为正方形的“渐开线”，则点A2021的坐标是　 　．

14．如图，将△ABC绕点A逆时针旋转45°得到△AB'C'，AB＝2，则图中阴影部分的面积为　 　．

15．如图，在矩形ABCD中，BC＝1，以点A为圆心，以AD长为半径画弧交BC于点E，∠DAE＝60°，则图中阴影部分的面积为　 　．

16．如图，在平面直角坐标系xOy中，等边△ABC的顶点A在y轴的正半轴上，B（﹣5，0），C（5，0），点D（11，0），将△ACD绕点A顺时针旋转60°得到△ABE，则的长度为　 　，线段AE的长为　 　，图中阴影部分面积为　 　．

17．如图，C是半圆上一点，AB是直径，将弧BC沿BC翻折交AB于点D，再将弧BD沿BD翻折交BC于点E，若E是弧BD的中点，AD＝2，则阴影部分面积为　 　．

18．已知圆锥的底面圆的半径为1，母线长为3，其侧面展开图的圆心角是　 　．
19．已知圆锥的底面圆半径为3cm，高为4cm，则母线长为　 　cm，圆锥的侧面积为　 　cm2．
20．如图，AB是⊙O的一条弦，OD⊥AB，垂足为C，OD交⊙O于点D，点E在⊙O上，
（1）若∠AOD＝50°，求∠DEB的度数；
（2）若OC＝3，OA＝5，
①求弦AB的长；
②求劣弧AB的长．



21．如图，四边形ABCD是⊙O的内接四边形，四边形ABCD两组对边的延长线分别相交于点E、F，且∠E＝40°，∠F＝50°，连接BD．
（1）求∠A的度数；
（2）当⊙O的半径等于2时，请直接写出的长（结果保留π）


22．如图，已知AB是⊙O的直径，C，D是⊙O上的点，OC∥BD，交AD于点E，连结BC．
（1）求证：AE＝ED；
（2）若AB＝6，∠ABC＝30°，求图中阴影部分的面积．


23．如图，在菱形ABCD中，对角线AC，BD交于点O，∠BAO＝30°，AC＝8．过点O作OH⊥AB于点H，以点O为圆心，OH为半径的半圆交AC于点M．
（1）求图中阴影部分的面积；
（2）点P是BD上的一个动点（点P不与点B，D重合），当PH+PM的值最小时，求PD的长度．



24．在扇形OAB中，C是弧AB上一点，延长AC到D，且∠BCD＝75°．
（1）求∠AOB的度数；
（2）扇形OAB是某圆锥的侧面展开图，若OA＝12，求该圆锥的底面半径．



25．如图，正方形ABCD内接于⊙O，P为上一点，连接DE，AE．
（1）∠CPD＝　 　°；
（2）若DC＝4，CP＝，求DP的长．


参考答案
1．解：如图，连接AE，EI，AH，过点J作JM⊥EI于M．

∵ABCDEF是正六边形，
∴∠DEF＝∠F＝120°，
∵FA＝FE，
∴∠FEA＝∠FAE＝30°，
∴∠AED＝90°，
同法可证，∠DEI＝∠EIH＝90°，
∴∠AED+∠DEI＝180°，
∴A，E，I共线，
设IH＝IJ＝JE＝a，
∵JM⊥EI，
∴EM＝MI＝a，
∴AI＝2EI＝2a，
∵∠API＝∠AHI，
∴tan∠API＝tan∠AHI＝＝＝2，
故选：A．
2．解：∵正六边形的半径等于边长，
∴正六边形的边长a＝3，
正六边形的周长l＝6a＝18，
故选：A．
3．解：弧长为：＝2π（cm）．
故选：B．
4．解：如图，连接OB．

∵CD⊥AB，CD是直径，
∴＝，
∴∠AOC＝∠BOC，
∵OA＝OB，
∴∠A＝∠B＝30°，
∴∠AOB＝180°﹣30°﹣30°＝120°，
∴∠COB＝∠AOB＝60°，
∴∠DOB＝180°﹣60°＝120°，
∴的长＝＝2π，
故选：B．
5．解：△ABC中，∠C＝90°，∠B＝30°，AC＝1，
所以BC＝AC＝，∠A＝60°，
∴S阴影＝S△ABC﹣S扇形ACD
＝×1×﹣＝﹣．
故选：B．
6．解：连接OC，AD
∵∠ACD＝30°，
∴∠AOD＝60°，
∵OA＝OD，
∴△AOD是等边三角形，
∵AB⊥CD，
∴OA平分CD，
∴CE＝DE＝CD＝，
∵CD垂直平分OA，
∴四边形ACOD是菱形，
在Rt△ACE中，AC＝＝＝2，
∴阴影部分面积＝＝π．
故选：A．

7．解：延长CD，DA交⊙O于E，F，

由对称性可知，图中阴影部分的面积＝×（S圆O﹣S正方形ABCD）＝×（9π﹣4）＝π﹣1，
故选：B．
8．解：根据题意，这个圆锥的全面积＝×2π×6×10+π×62＝60π+36π＝96π（cm2）．
故选：B．
9．解：设扇形的圆心角为n，圆锥的顶点为B，
∵r＝20cm，h＝20cm，
∴由勾股定理可得母线l＝＝80（cm），
而圆锥侧面展开后的扇形的弧长为2×20π＝，
∴n＝90°，
即△BAA′是等腰直角三角形，
由勾股定理得：AA'＝＝80（cm）．
∴蚂蚁爬行的最短距离为80cm．
故选：D．

10．解：连接OB，OC，
∵正方形ABCD内接于⊙O，
∴∠BOC＝90°，
∴∠BEC＝90°÷2＝45°．
当点E′在劣弧BC上时，∠BE′C＝180°﹣∠BAEC＝135°
故答案为：45°或135°．

11．解：如图：连接OA，OB，OG，OH．
∵△AOB为等边三角形，
∴T1的半径为R，
在Rt△OAG和Rt△OBG中，
，
Rt△OGB≌Rt△OGA（HL），
∴∠OGB＝∠OGA＝60°，
∴BG＝OG，
设BG为x，由勾股定理有：x2+R2＝（2x）2，
解得：x＝R，
外切正六边形的边长为R，
∵阴影部分的面积＝外切正六边形的面积﹣内接正六边形的面积，
又∵内接正六边形的面积为S△AOB的六倍，S△AOB＝R2，
∴内接正六边形的面积为：S内＝6×R2＝R2，
∵外切正六边形的面积为S△OGH的六倍，S△OHG＝•（R）2＝R2，
∴外切正六边形的面积为：S外＝6×R2＝2R2，
∴S阴＝S外′﹣S内＝2R2﹣R2＝R2．

12．解：∵△ABC是正三角形，
∴∠A＝∠B＝∠C＝60°，
∴的长＝＝（cm），
则弧三角形的周长＝×3＝2π（cm），
故答案为：2π．
13．解：A（1，1），
由题意得，A1（2，0），A2（0，﹣2），A3（﹣3，1），A4（1，5），
A5（6，0），A6（0，﹣6），A7（﹣7，1），A8（1，9）…，
∴A4n（1，4n+1），A4n+1（4n+2，0），A4n+2（0，﹣（4n+2）），A4n+3（﹣（4n+3），1）．
∵2021＝505×4+1，
∴A2021的坐标为（2022，0）．
故答案为：（2022，0）．
14．解：作B′D⊥AB于D，
∵△ABC绕点A逆时针旋转45°得到△AB'C'，AB＝2，
∴△AB′C′的面积＝△ABC的面积，∠BAB′＝45°，AB＝AB′＝2，
∴B′D＝AB′＝，
∴S△ABB′＝＝＝，
∵图中阴影部分的面积＝△AB′C′的面积+△AB′B的面积﹣△ABC的面积＝△AB′B′的面积，
∴S阴影＝，
故答案为：．

15．解：∵四边形ABCD是矩形，
∴AD＝BC＝1，AD∥BC，
∴∠AEB＝∠DAE＝60°，
∵∠B＝90°，AE＝AD＝1，
∴AB＝AE•sin60°＝，
∴S阴＝S矩形ABCD﹣S扇形ADE＝﹣＝﹣，
故答案为﹣．
16．解：∵等边△ABC的顶点A在y轴的正半轴上，
∴OB＝OC，
∵B（﹣5，0），C（5，0），
∴OB＝OC＝5，AB＝AC＝BC＝10，
∴OA＝＝5，
∵D（11，0），
∴OD＝11，
∴AD2＝AO2+OD2＝75+121＝196，
∵△ACD绕点A顺时针旋转60°得到△ABE，
∴∠DAE＝60°，AE＝AD＝＝14；
∴的长度为＝π；
∴图中阴影部分面积
＝S扇形DAE﹣S扇形BAC＝π×AD2﹣π×AC2＝π（196﹣100）＝16π．
故答案为：π；14；16π．
17．解：如图，连接AC，CD，DE，OE，过点C作CH⊥AB于H，过点D作DJ⊥CE于J．

∵∠ABC＝∠DBC＝∠DBE，
∴＝＝，
∴AC＝CD＝DE，
∵CH⊥AD，DJ⊥CE，
∴AH＝HD，CJ＝JE，
∵E是的中点，
∴＝，
∴ED＝EB，
∴∠EDB＝∠EBD，
设∠EDB＝∠EBD＝x，则∠DEC＝∠DCE＝∠EDB+∠EBD＝2x，
∴∠A＝∠CDA＝∠DCE+∠EBD＝3x，
∵AB是直径，
∴∠ACB＝90°，
∴∠A+∠B＝90°，
∴3x+x＝90°，
∴x＝22.5°，
∴∠A＝∠CDA＝67.5°，
∵CA＝CD，CH⊥AD，
∴∠ACH＝∥DCH＝22.5°，
在CH上取一点T，使得CT＝DT，连接DT，
∴∠TCD＝∠TDC＝22.5°，
∴∠HTD＝∠TCD+∠TDC＝45°，
∵∠THD＝90°，
∴∠HTD＝∠HDT＝45°，
∴HT＝DH＝1，DT＝TC＝，
∴CH＝1+，
∴CD2＝CH2+DH2＝（1+）2+12＝4+2，
∵∠DCE＝2x＝45°，
∴∠DCE＝∠DEC＝45°，
∴△DCE是等腰直角三角形，
∵弓形AmC的面积＝弓形DmE的面积，
∴S阴＝S四边形ACED＝S△ACD+S△CDE＝•AD•CH+CD2＝×2×（1+）+×（4+2）＝3+2，
故答案为：3+2．
18．解：圆锥侧面展开图的弧长是：2π×1＝2π（cm），
设圆心角的度数是n度，
则＝2π，
解得：n＝120．
故答案为：120°．
19．解：根据题意可得，
这个圆锥的母线长＝＝5（cm），
这个圆锥的侧面积＝•2π•3•5＝15π（cm2）．
故答案为：5，15π．
20．解：（1）∵OD⊥AB，
∴＝，
∴∠DEB＝∠BOD＝∠AOD＝×50°＝25°．

（2）①∵OC＝3，OA＝5，
∴AC＝4，
∵OD⊥AB，
∴＝＝，
∴AC＝BC＝AB＝4，
∴AB＝8；
②∵∠AOD的正弦值是＝＝0.8，
∴∠AOD＝53°，
∴∠AOB＝106°，
∵OA＝5，
∴的长＝＝＝．
21．解：（1）∵四边形ABCD是⊙O的内接四边形，
∴∠DCE＝∠A，
∵∠EDF＝∠A+∠F＝∠A+50°，
而∠EDF+∠DCE+∠E＝180°，
∴∠A+50°+∠A+40°＝180°，
∴∠A＝45°；
（2）连接OB、OD，如图，
∵∠BOD＝2∠A＝90°，
∴的长＝＝π．

22．（1）证明：∵AB是⊙O的直径，
∴∠ADB＝90°，
∵OC∥BD，
∴∠AEO＝∠ADB＝90°，即OC⊥AD，
又∵OC为半径，
∴AE＝ED，
（2）解：连接CD，OD，
∵OC＝OB，
∴∠OCB＝∠ABC＝30°，
∴∠AOC＝∠OCB+∠ABC＝60°，
∵OC⊥AD，
∴＝，
∴∠COD＝∠AOC＝60°，
∴∠AOD＝120°，
∵AB＝6，
∴BD＝3，AD＝3，
∵OA＝OB，AE＝ED，
∴OE＝＝，
∴S阴影＝S扇形AOD﹣S△AOD＝﹣×＝3π﹣．

23．解：（1）∵四边形ABCD是菱形，
∴AC⊥BD，OA＝OC＝4，
∵OH⊥AB，
∴∠AHO＝90°，
∵∠OAH＝30°，
∴∠AOH＝60°，OH＝OA＝2，AH＝OH＝2，
∴S阴＝S△AOH﹣S扇形OMH＝×2×2﹣＝2﹣π．
（2）作点M关于B的对称点M′，连接HM′交BD于P，连接PM，连接PM，此时PH+PM的值最小．
∵OH＝OM′，
∴∠OHM′＝∠OM′H，
∵∠AOH＝∠OHM′+∠OM′H＝60°，
∴OP＝OM′•tan30°＝，
∵OD＝OA•tan30°＝，
∴PD＝OD+OP＝+＝2．

24．解：（1）作出所对的圆周角∠APB，
∵∠APB+∠ACB＝180°，∠BCD+∠ACB＝180°，
∴∠APB＝∠BCD＝75°，
∴∠AOB＝2∠APB＝150°；
（2）设该圆锥的底面半径为r，
根据题意得2πr＝，解得r＝5，
∴该圆锥的底面半径为5．

25．解：（1）如图，连接BD，
∵正方形ABCD内接于⊙O，P为上一点，
∴∠DBC＝45°，
∵∠CPD＝∠DBC，
∴∠CPD＝45°．
故答案为：45；
（2）如图，作CH⊥DP于H，
∵CP＝2，∠CPD＝45°，
∴CH＝PH＝2，
∵DC＝4，
∴DH＝＝＝2，
∴DP＝PH+DH＝2+2．