高中数学人教版新课标B选修1-11.1.2量词课前预习ppt课件

这是一份高中数学人教版新课标B选修1-11.1.2量词课前预习ppt课件，共18页。PPT课件主要包含了新知探求，课堂探究，知识点一，特称命题，全称命题的否定，知识点二，特称命题的否定，∀x∈M¬px，全称命题，题型一等内容，欢迎下载使用。

新知探求 素养养成
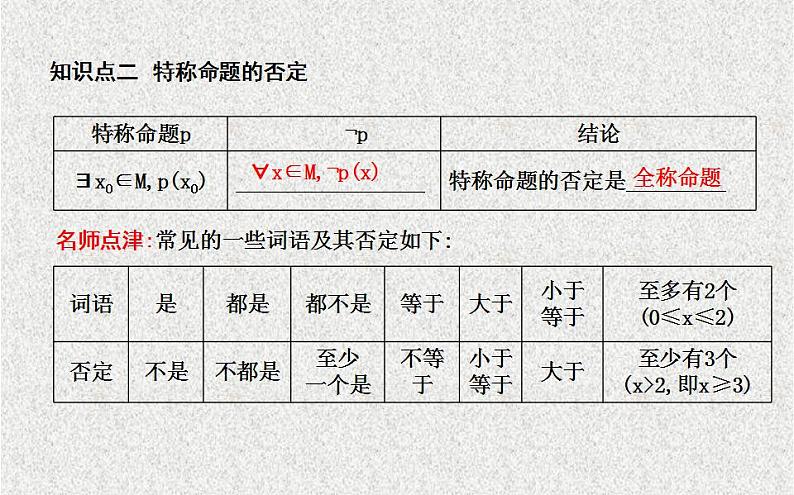
∃x0∈M,¬p(x0)
名师点津:常见的一些词语及其否定如下:
全称命题的否定及其真假判断
课堂探究 素养提升
【例1】 写出下列全称命题的否定并判断其真假:(1)不论m取何实数,方程x2+x-m=0必有实数根;
解:(2)命题的否定是:存在末位数字是0或5的整数不能被5整除,是假命题.
(4)全称命题,它的否定是特称命题,¬ q:至少存在一个正方形不是矩形,假命题.
方法技巧 对全称命题否定的步骤(1)改变量词:把全称量词改为恰当的存在量词,对省略全称量词的全称命题可补上量词.(2)否定性质:把全称命题的结论否定.
即时训练1:写出下列全称命题的否定:(1)p:所有能被3整除的整数都是奇数;(2)p:每一个四边形的四个顶点共圆;(3)p:对任意x∈Z,x2的个位数字不等于3.
解:(1)¬p:存在一个能被3整除的整数不是奇数.(2)¬p:存在一个四边形,它的四个顶点不共圆.
【备用例1】 命题“任意x∈R,若y>0,则x2+y>0”的否定是　　　　　　. 
特称命题的否定及其真假判断
解:(1)命题的否定:任一个梯形的对角线都不互相平分,是真命题.(2)特称命题,它的否定是全称命题,¬r:∀x∈R,x2+2x+2>0,真命题.(3)特称命题,它的否定是全称命题,¬s:∀x∈R,x3+1≠0,假命题,例如x=-1,x3+1=0.
方法技巧 对特称命题否定的步骤(1)改变量词:把存在量词改为恰当的全称量词.(2)否定性质:把特称命题的结论否定.
即时训练2:(2018·蚌埠高二月考)设x∈Z,集合A是奇数集,集合B是偶数集.若命题p:∀x∈A,2x∈B,则(　　)(A)¬p:∃x∈A,2x∈B(B)¬p:∃x∉A,2x∈B(C)¬p:∃x∈A,2x∉B(D)¬p:∀x∉A,2x∉B
解析:命题p:∀x∈A,2x∈B是一个全称命题,其命题的否定¬p应为∃x∈A,2x∉B,故选C.
【例3】 若∀x∈R,函数f(x)=mx2+x-m-a的图象和x轴恒有公共点,求实数a的取值范围.
解:(1)当m=0时,f(x)=x-a与x轴恒相交,所以a∈R.(2)当m≠0时,二次函数f(x)=mx2+x-m-a的图象和x轴恒有公共点的充要条件是Δ=1+4m(m+a)≥0恒成立,即4m2+4am+1≥0恒成立.又4m2+4am+1≥0是一个关于m的二次不等式,恒成立的充要条件是Δ=(4a)2-16≤0,解得-1≤a≤1.综上所述,当m=0时,a∈R;当m≠0,a∈[-1,1].
解:(1)当m=0时,f(x)=x-a与x轴恒相交,所以a∈R.(2)当m≠0时,二次函数f(x)=mx2+x-m-a的图象和x轴有公共点的充要条件是Δ=1+4m(m+a)≥0成立,即4m2+4am+1≥0成立.所以16a2-16≥0.当m≠0,a∈(-∞,-1]∪[1,+∞).综上所述,当m=0时,a∈R,当m≠0时,a∈(-∞,-1]∪[1,+∞).
摇身一变:若∃x∈R,函数f(x)=mx2+x-m-a的图象和x轴有公共点,求实数a的取值范围.
方法技巧 对于“至多”“至少”命题,或命题为假命题的命题求参数,通常先考虑命题的否定,求出相应的集合,再求其补集.
即时训练3:(2018·厦门质检)若命题“存在实数x,使x2+ax+1<0”的否定是假命题,则实数a的取值范围为　　　　. 
解析:依题意“存在实数x,使x2+ax+1<0”是真命题,所以方程x2+ax+1=0有不等的实根,所以Δ=a2-4>0,得a<-2或a>2.答案:(-∞,-2)∪(2,+∞)