数学人教版（中职）9.2 空间中的平行关系教课ppt课件

这是一份数学人教版（中职）9.2 空间中的平行关系教课ppt课件，共17页。PPT课件主要包含了公理4，等角定理，平行和相交两种，空间中有几种呢，不一定，“不共面”的认识，or“异面”，相交直线，平行直线，异面直线等内容，欢迎下载使用。

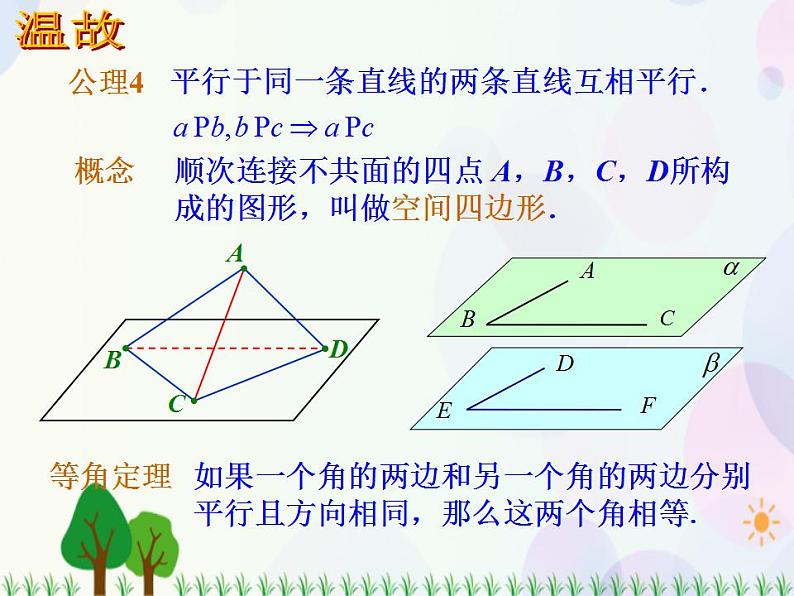
平行于同一条直线的两条直线互相平行．
顺次连接不共面的四点 A，B，C，D所构成的图形，叫做空间四边形．
如果一个角的两边和另一个角的两边分别平行且方向相同，那么这两个角相等.
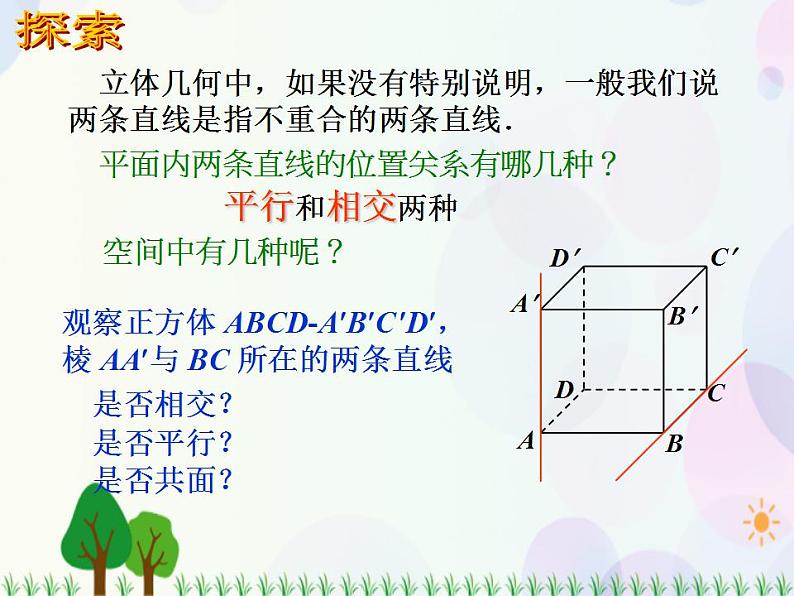
观察正方体 ABCD-ABC D，棱 AA与 BC 所在的两条直线 是否相交？ 是否平行？ 是否共面？
平面内两条直线的位置关系有哪几种？
　立体几何中，如果没有特别说明，一般我们说两条直线是指不重合的两条直线．
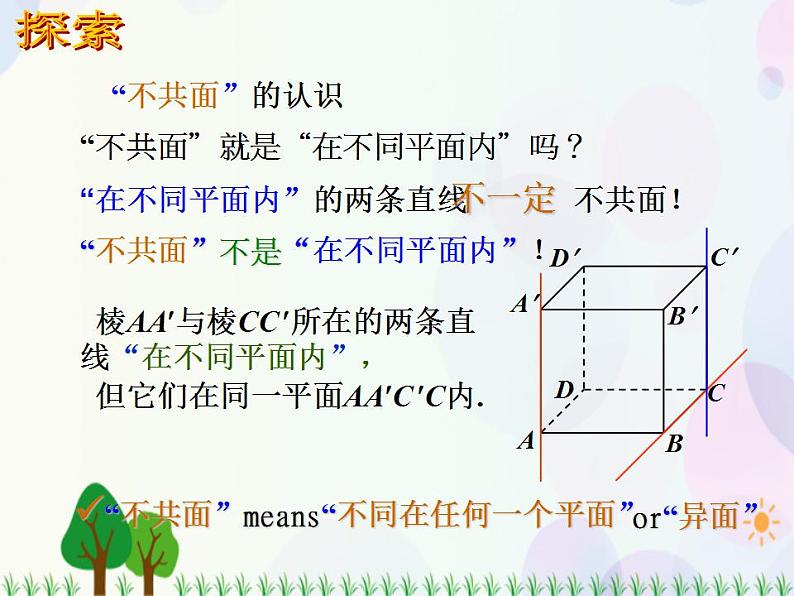
“在不同平面内”的两条直线 不共面！
棱AA与棱CC 所在的两条直线“在不同平面内”， 但它们在同一平面AAC C内.
“不共面”就是“在不同平面内”吗？
“不共面”means“不同在任何一个平面”
“不共面”不是“在不同平面内”！
空间中两条直线的位置关系　
两条相交直线与平行直线又叫共面直线.
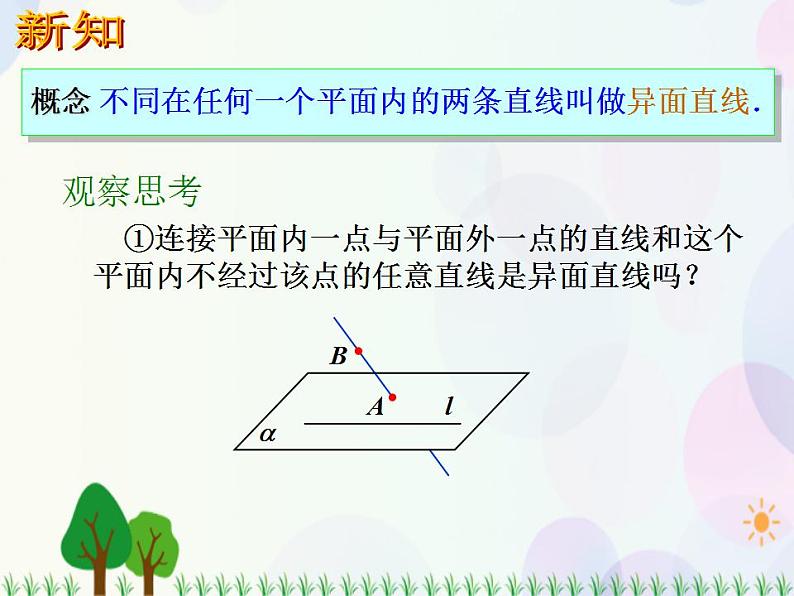
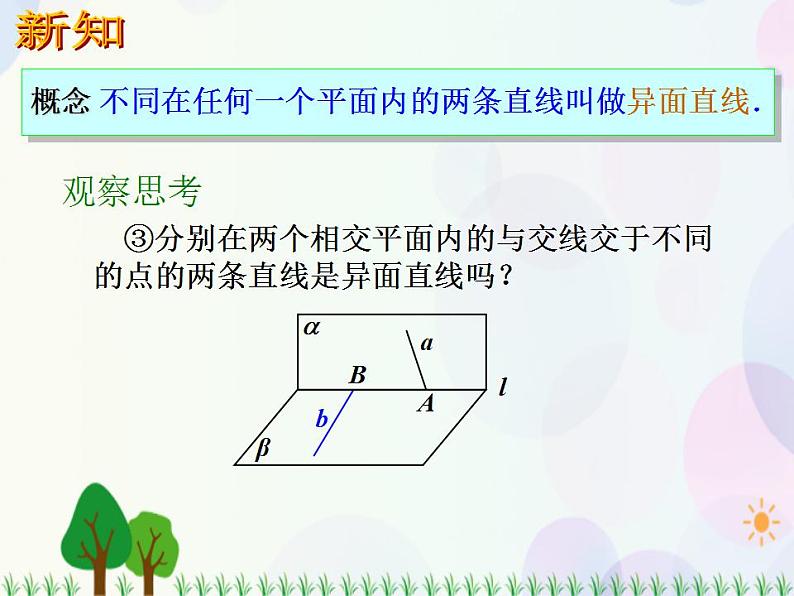
不同在任何一个平面内的两条直线叫做异面直线．
①连接平面内一点与平面外一点的直线和这个平面内不经过该点的任意直线是异面直线吗？
②与平面平行的直线和这个平面内与它不平行的直线是异面直线吗？
③分别在两个相交平面内的与交线交于不同的点的两条直线是异面直线吗？
异面直线常常这样借助一个或两个平面的衬托来画出.
1.在如图所示的是正方体 ABCD-ABC D中，哪些棱所在的直线与直线 BA是异面直线？　
解：与直线 BA异面的直线有:
BC，AD，CC，DC，DC，DD.
哪些棱所在的直线与直线 AB 是异面直线？
(1)这些直线与直线a 的角度相同吗？
(2)如何来定义两条异面直线所成的角呢?
为了简便，点O常取在两条异面直线中的一条上．
如线段的端点，线段的中点等．
直线a、b是异面直线，
经过空间任意一点O，分别引直线a′∥a , b′∥b.
直线a′和b′所成的锐角或直角叫做异面直线a和b所成的角.
当两条异面直线a、b的夹角为直角时，称这两条异面直线垂直，
解：(1)因为BB∥CC ，所以 BBA为异面直线BA与CC 所成的角．
2.如图所示的是正方体 ABCD-ABC D中，(1) 求直线BA与CC 所成的角的度数； (2) 哪些棱所在的直线与直线AA垂直？
因此BA与CC 所成的角为45；
(2) 与直线AA垂直的直线有AB，BC，CD，DA，AB，BC ，C D，DA．
① 求第一小题中的异面角度数你还有其他方法吗？ ② “过一点有且只有一条直线与已知直线垂直”对吗？
已知ABCD-ABC D是棱长为a的正方体(1)求异面直线AA与BC所成的角；(2)求异面直线BC 和AC所成的角.
求异面角一般步骤怎样？
一 平移，二 证明，三 计算，四 作答．
3.在空间四边形ABCD中，AD=BC=2a，点E、F分别是AB、CD的中点，EF= ，求AD和BC所成的角.
取AC的中点M，连结EM、FM，
EM∥BC，EM=a，
FM∥AD，FM=a，
在△EMF中EM=FM=a，EF=
∵EM2+FM2=EF2=2a2，
∴ ∠EMF是异面直线AD和BC所成的角.
故AD和BC所成的角为90
在空间四边形ABCD中，DA=BC, DA⊥BC, 点E、F分别为DC、AB 的中点，求异面直线EF与DA 所成的角.