高中数学人教版（中职）基础模块下册第十章 概率与统计初步10.3 统计初步图片课件ppt

这是一份高中数学人教版（中职）基础模块下册第十章 概率与统计初步10.3 统计初步图片课件ppt，共39页。PPT课件主要包含了学习目标，内容提要，例1已知，练习1，性质1，性质3，性质2，日产量件xi，工人人数fi，练习4等内容，欢迎下载使用。
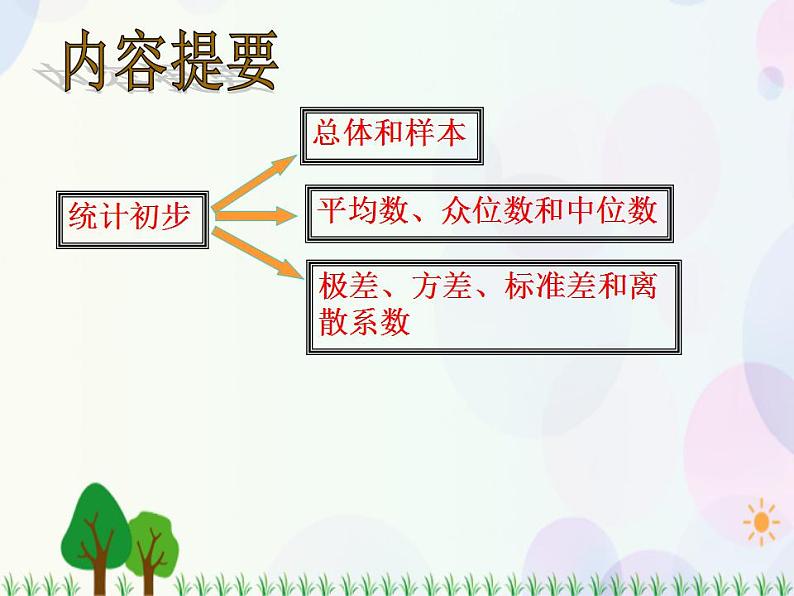
理解总体、样本、样本容量的概念； 能正确确定考察对象的总体、样本 和样本容量； 了解求和符号“ ”的意义 理解平均数、加权算术平均数、众 数和中位数的概念； 会求平均数、加权算术平均数、众 数和中位数；
理解极差、方差、标准差和离散系数的概念.会求一组数据的极差、方差、标准差 和离散系数；会运用方差、标准差或离散系数判断 一组数据的稳定程度
10.3.1 总体和样本
在统计知识中，我们把所要考察对象的全体叫做总体，其中的每一个考察对象叫做个体，从总体中所抽取的一部分个体叫做总体的一个样本，样本中个体的数目叫做样本容量.
例如 在考察某批灯泡的平均使用寿命时，该批灯泡寿命的全体就是一个总体，其中每一个灯泡寿命就是个体.
一般地，为了考察总体 ，从总体中抽取n个个体来进行试验或观察，这n个个体是来自总体 的一个样本,n为样本容量.
例如 2008年人口普查中，当考察我国人口年龄构成时，总体就是所有具有中华人民共和国国籍并在中华人民共和国国内常住的人口的年龄；个体就是符合这一条件的每一个公民的年龄；符合这一条件的所有广州的市民的年龄就是一个样本.在这个样本中，广州的市民的人数就是这个样本的容量.
练习1：某大型购物商场为了了解会员多长时间会到本商场购买一次商品，而组织市场调查。在持有该公司会员卡的所有135000名顾客中随机挑选了500名顾客进行电话询问，请指出本次市场调查对象的总体、样本和样本容量。
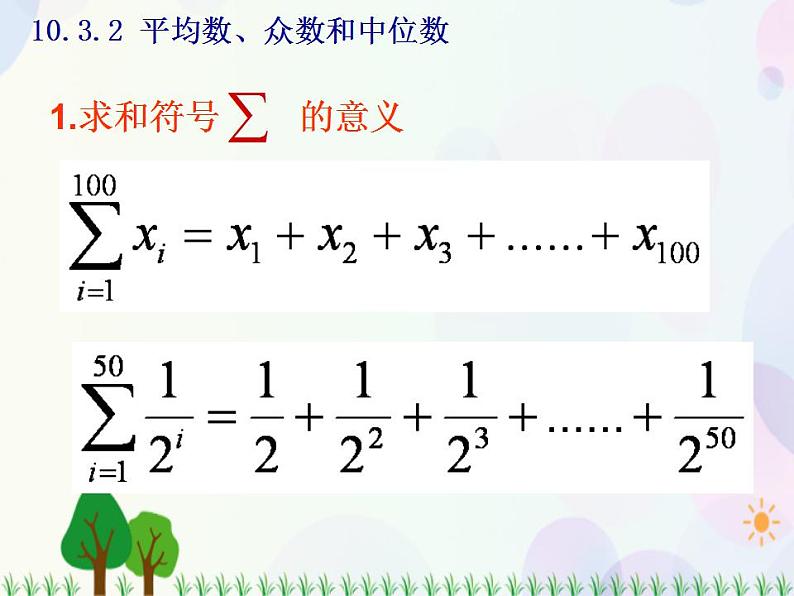
1.求和符号 的意义
10.3.2 平均数、众数和中位数
用求和符号 表示下列各和式
10.3.2 平均数、众数和中位
1*.求和符号 的性质
例2* 已知x1=5, x2=8, x3=9, x4=6
10.3.2平均数、众数和中位数
练习2：已知x1=15, x2=18, x3=10, x4=－16
2.平均数与加权平均数
有n个数据x1, x2, x3,…..,x n,计算平均数的公式为：
例2 华美公司某生产组6名工人生产同一种零件的日产量分别为：66、68、69、71、72、74.求这组数据的平均数。
练习3：数据80，84，85，90，90，91，93中的平均数是多少?
若按照“平时成绩占30%、期中成绩占30%、期末成绩占40%”的比例计算，李亮同学数学课程平时成绩为80分、期中成绩为70分、期末成绩为90分。那么他这学期数学的总评成绩就应该为：这样求出来的数就是统计中常用到的另一种数平均数——加权算术平均数.
80×30%+70×30%+90×40%=81
一般地，把各指标在总结果中所占的百分比称为每个指标获得的权重，各指标乘以相应的权重后所得的平均数叫做加权平均数，计算公式为：
例3 力特公司某生产组10名工人生产汽车零件，日产量分组资料如下表所示，计算工人的平均日产量.
根据资料，可以计算该生产组10名工人的平均日产量为
答：该公司工人的平均日产量为26件.
刘军同学在这学期的前四次数学测验中得分依次是95、83、77、86，马上要进行第五次测验了，他希望五次成绩的平均数能够达到或超过85分，那么，这次测验他至少要考多少分？
一组数据中，出现次数最多的那个数据值叫做这组数据的众数.用符号 表示.如果有两个数据并列最多，那么这两个值都是众数. 所以，一组数据可以有不止一个众数，也可以没有众数.
例5 2006级财会某班第2小组同学的身高如下:1.57，1.53，1.56，1.70，1.60，1.68,1.61，1.64.求这组数据的中位数（单位：米）
练习5：数据80，84，85，90，90，91，93中的中位数和众数各是多少？
一般地，我们将变量分布中最大值与最小值之差叫做极差，也叫全距.用符号R表示.
极差（R）= 最大变量值－最小变量值
10.3.3 极差、方差、标准差和离散系数
例1 已知某次A组5名学生数学考试成绩为67，69，70，71，73；B组5名学生数学考试成绩为：41，68，70，81，90，试求两组学生的平均成绩,并比较两组学生考试成绩的均衡程度.
分析：虽然两个组的平均成绩相同，都是70分，但是各组成绩离散程度不同.A组学习成绩比较平衡，平均数的代表性高，而B组成绩差别大，平均数的代表性低.

例2 已知某次A组5名学生数学考试成绩为：67，69，70，71，73；B组5名学生数学考试成绩为：41，68，70，81，90，试求每组学生成绩的平均差.
解：A组平均差： B组平均差：
练习1 已知某次A组5名学生语文考试成绩为：77，79，80，81，83；B组5名学生数学考试成绩为：51，78，82，91，98，试求每组学生成绩的平均差.
一组数据中各数据值与该组数据的平均数的离差的平方的算术平均数，叫做方差；用符号 表示. 设有n个数据x1,x2,x3,….,xn ，则其方差计算公式为：
例3 佳乐公司一班二组10名工人日组装机器件数为：5，7，7，8，8，8，8，10，11，12，试求该组工作组装机器件数的标准差.
练习2 佳乐公司一班三组10名工人日组装机器件数为：48，50，51，52，52，53，54，56，56，56，试求该组工作组装机器件数的标准差.
标准差与相应算术平均数的比值叫做离散系数，又叫变动系数.离散系数的计算公式为：
解:A企业： B企业： 所有B企业的平均工资离散程度小.
例4 上海A企业九月员工的平均工资是3000元，标准差为180元，该月B企业员工的平均工资是3600元，标准差为200元.问哪个企业平均工资离散程度小.