初中数学华师大版八年级上册第13章 全等三角形13.4 尺规作图3 作已知角的平分线精品巩固练习

13.4.3作已知角的平分线同步练习华师大版初中数学八年级上册

一、选择题（本大题共12小题，共36.0分）

1. 如图，用三角尺可按下面方法画角平分线：在已知的的两边上分别取点M、N，使，再分别过点M、N作OA、OB的垂线，交点为P，画射线可证得≌，OP平分以上依画法证明≌根据的是   

A. SSS B. HL C. AAS D. SAS

2. 如图1，已知，用尺规作它的角平分线．
   如图2，步骤如下，
   第一步：以B为圆心，以a为半径画弧，分别交射线BA，BC于点D，E；
   第二步：分别以D，E为圆心，以b为半径画弧，两弧在内部交于点P；
   第三步：画射线射线BP即为所求．
   下列正确的是

A. a，b均无限制 B. ，的长
C. a有最小限制，b无限制 D. ，的长

3. 如图，，以点A为圆心，小于AC长为半径作圆弧，分别交AB，AC于点E，F，再分别以E，F为圆心，大于长为半径作圆弧，两弧交于点P，连接AP并延长交CD于点M，若，则的度数为   

A.  B.  C.  D.

4. 尺规作图作角的平分线，作法步骤如下：
    

以点O为圆心，任意长为半径画弧，交OA、OB于C、D两点；

分别以C、D为圆心，大于长为半径画弧，两弧交于点P；

过点P作射线OP，射线OP即为所求．

则上述作法的依据是．

A. SSS B. SAS C. AAS D. ASA

5. 作的平分线的作图过程如下：
   
   做法如上图：
   在OA和OB上分别截取OD，OE，使．
   分别以D，E为圆心、以大于的长为半径作弧，两弧在内交于点C．
   作射线OC，则OC就是的平分线．

用下面三角形全等的判定方法解释作图原理，其中最为恰当的是   

A. 边角边 B. 角边角 C. 角角边 D. 边边边

6. 如图，用直尺和圆规作一个角的平分线，是运用了“全等三角形的对应角相等”这一性质，由作图所得条件，判定三角形全等运用的方法是

A. SAS B. ASA C. AAS D. SSS

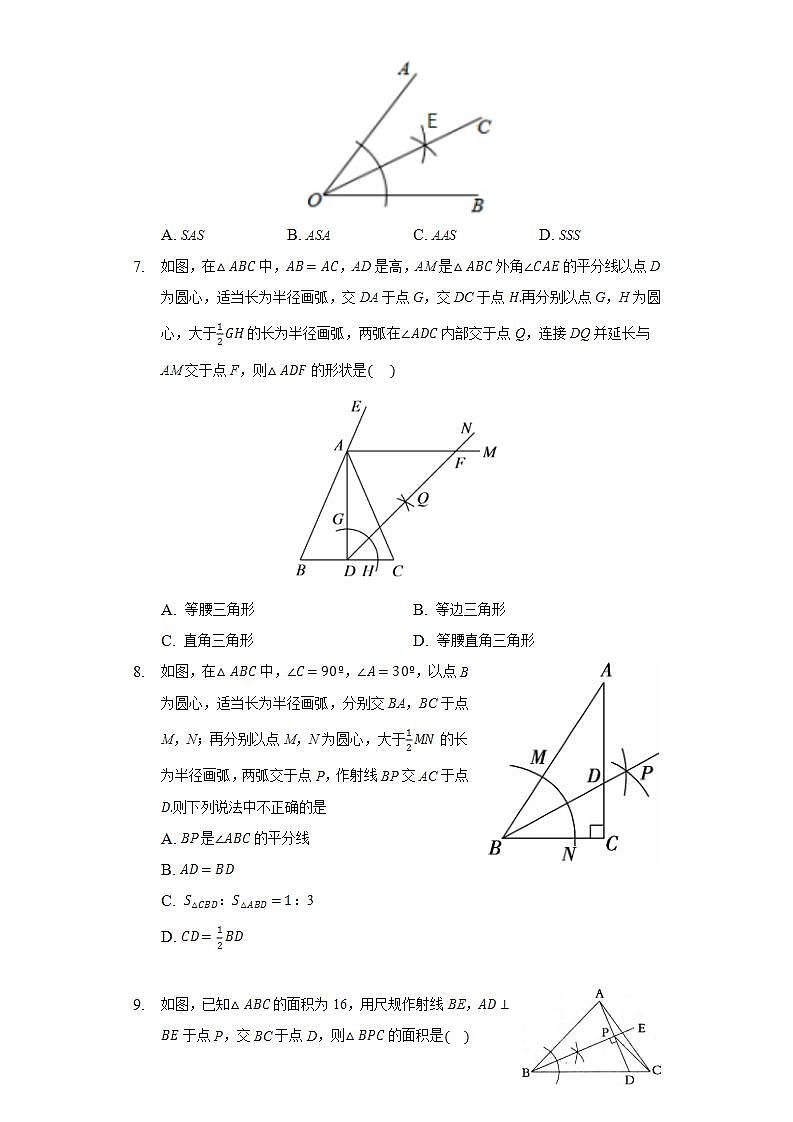
7. 如图，在中，，AD是高，AM是外角的平分线以点D为圆心，适当长为半径画弧，交DA于点G，交DC于点再分别以点G，H为圆心，大于的长为半径画弧，两弧在内部交于点Q，连接DQ并延长与AM交于点F，则的形状是   

A. 等腰三角形 B. 等边三角形
C. 直角三角形 D. 等腰直角三角形

8. 如图，在中，，，以点B为圆心，适当长为半径画弧，分别交BA，BC于点M，N；再分别以点M，N为圆心，大于的长为半径画弧，两弧交于点P，作射线BP交AC于点则下列说法中不正确的是

A. BP是的平分线
B.
C. ：：3
D.
 

9. 如图，已知的面积为16，用尺规作射线BE，于点P，交BC于点D，则的面积是

A. 12
B. 8
C. 6
D. 4

10. 如图，在中，，AD是高，AM是外角的平分线．以点D为圆心，适当长为半径画弧，交DA于点G，交DC于点再分别以点G、H为圆心，大于的长为半径画弧，两弧在内部交于点Q，连接DQ并延长与AM交于点F，则的形状是   

A. 等腰三角形 B. 等边三角形
C. 直角三角形 D. 等腰直角三角形

11. 如图，用尺规作已知角的平分线的理论依据是

A. SAS
B. AAS
C. SSS
D. ASA

12. 如图，在中，，AD是高，AM是外角的平分线．以点D为圆心，适当长为半径画弧，交DA于点G，交DC于点再分别以点G、H为圆心，大于的长为半径画弧，两弧在内部交于点Q，连接DQ并延长与AM交于点F，则的形状是

A. 等腰三角形 B. 等边三角形
C. 直角三角形 D. 等腰直角三角形

二、填空题（本大题共5小题，共15.0分）

13. 如图所示，，以点O为圆心，以适当长为半径作弧分别交OA，OB于C，D两点；分别以C，D为圆心，以大于的长为半径作弧，两弧相交于点P；以O为端点作射线OP，在射线OP上取点M，连接MC、若测得，则______
14. 如图所示，，以点O为圆心，以适当长为半径作弧分别交OA，OB于C，D两点；分别以C，D为圆心，以大于的长为半径作弧，两弧相交于点P；以O为端点作射线OP，在射线OP上取点M，连接MC、若测得，则_____
15. 如图，已知，求作射线OC，使OC平分，那么作法的合理顺序是______．
    作射线OC；
    在OA和OB上分别截取OD，OE，使；
    分别以D，E为圆心，大于的长为半径作弧，在内，两弧交于C．
16. 如图，在中，以点B为圆心，适当长为半径画弧，交BA，BC于点D，E，再分别以D，E为圆心，大于长为半径画弧，两弧交于点F，作射线BF交AC于点现测得，，那么的度数为______．
     

17. 如图，在的两边OA，OB上分别截取OM，ON，使；再分别以点M，N为圆心，以大于的长为半径作圆弧，两弧交于点E，过点E作于点若，则点E到直线OB的距离是________．

三、解答题（本大题共6小题，共48.0分）

18. 如图：已知，要求保留作图痕迹，不写作法
     

求作：的平分线OC．

 作射线．

在OC上取一点P，作出点P到两边的垂线段，并比较这两条垂线段的大小关系？证明你的结论．






 

19. 人教版初中数学教科书八年级上册第48页告诉我们一种作已知角的平分线的方法：
    已知：．
    求作：的平分线．
    作法：以点O为圆心，适当长为半径画弧，交OA于点M，交OB于点N．
    分别以点M，N为圆心，大于的长为半径画弧，两弧在的内部相交于点C．
    画射线OC，射线OC即为所求如图．
    请你根据提供的材料完成下面问题．
    这种作已知角的平分线的方法的依据是______填序号
    
    请你证明OC为的平分线．
    
    
    
    
    
    
     
20. 如图，中，，．
    用尺规作图作的角平分线，交AC于点D；保留作图痕迹，不写作法．
    求证：是等腰三角形．
    
    
     

21. 如图，已知是的外角，
    作的平分线尺规作图，不写作法，保留作图痕迹；
    在的基础上，若，求证：．
    
    
    
    
     

22. 如图中，，，垂足为D，求作的平分线，分别交AD，AC于P，Q两点；并证明。要求：尺规作图，保留作图痕迹，不写作法

23. 如图，，，CD，分别是和的平分线，且．

用尺规作图，在中作出的平分线；不写作法，保留作图痕迹 

求证：．

答案和解析

1.【答案】B
 

【解析】解：由作法可得，，，
则，
在和中
，
所以≌．
故选B．
利用作法可得到，，，再加上公共边OP，则可利用“HL”判断≌．
本题考查了基本作图：熟练掌握基本作图作已知角的角平分线也考查了全等三角形的判定方法．
 

2.【答案】B
 

【解析】解：以B为圆心画弧时，半径a必须大于0，分别以D，E为圆心，以b为半径画弧时，b必须大于，否则没有交点，
故选：B．
根据角平分线的画法判断即可．
本题考查作图基本作图，解题的关键是熟练掌握五种基本作图，属于中考常考题型．
 

3.【答案】B
 

【解析】由作法得AM平分，
，
，
，
，
，
．
故选B．
 

4.【答案】A
 

【解析】

【分析】
本题考查作图基本作图，全等三角形的判定和性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题．
根据SSS证明三角形全等，利用全等三角形的性质解决问题即可．
【解答】
解：连接PC，PD．

由作图可知，，，
在和中，

，
，
即OP是的平分线．
因此题中作法的依据是SSS．
故选：A．  

5.【答案】D
 

【解析】如图，连接EC，DC．

在和中，

，

，

平分，故选D．

6.【答案】D
 

【解析】

【分析】
本题考查的是作图基本作图，全等三角形的判定，要清楚作图时作出的线段OD与OE、EF与DF是相等的，熟练掌握三角形全等的判定条件是解答此题的关键．易知：，，，因此符合SSS的条件．
【解答】
解：连接DF，EF，

由作图知：，，
在和中，
≌，
故选D．  

7.【答案】D
 

【解析】

【解答】
解：根据画图过程可知：
DF平分，
，
，
，
是外角的平分线，
，
，
，
，
，
，
，
是高，
，
，
的形状是等腰直角三角形．
故选：D．
【分析】
本题考查了作图基本作图、平行线的判定，等腰三角形的判定、等腰直角三角形，解决本题的关键是掌握画一个角的平分线的方法．
根据画图过程可得：DF平分，，根据，得，由AM是外角的平分线，证得，得，进而证明的形状．  

8.【答案】C
 

【解析】

【分析】
本题考查了作图基本作图：熟练掌握基本作图作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线利用基本作图可对A选项进行判断；计算出，则可对B选项进行判断；利用得到，则可对D选项进行判断；由于，则可根据三角形面积公式对C选项进行判断．
【解答】
解：由作法得BD平分，所以A选项的结论正确；
，，
，
，
，所以B选项的结论正确；
，
，即，所以D选项的结论正确；
，
，即：：2，所以C选项的结论错误．
故选C．  

9.【答案】B
 

【解析】

【分析】
本题考查尺规作图--作一个角的平分线，三角形的面积以及三角形全等的判定和性质，根据全等三角形的性质得到，，从而得出的面积是的面积的一半即可．
【解答】
解：由作图可知，BE平分，
，
又，
，
在和中，


，
，，
．
故选B．  

10.【答案】D
 

【解析】

【分析】
本题考查了作图基本作图、等腰三角形的判定、等边三角形的判定、等腰直角三角形，解决本题的关键是掌握画一个角的平分线的方法，根据画图过程可得：DF平分，，根据，得，由AM是外角的平分线，证得，得，进而证明的形状．
【解答】
解：根据画图过程可知：
DF平分，
，
，
，
是外角的平分线，
，
，
，
，
，
，
，
是高，
，
，
的形状是等腰直角三角形．
故选D．  

11.【答案】C
 

【解析】

【分析】
本题考查了尺规作图作角的平分线，全等三角形的性质和判定的应用。连接NC，MC，根据SSS证≌，即可推出答案。
【解答】
解：连接NC，MC

在和中，

≌

故选C。  

12.【答案】D
 

【解析】解：根据画图过程可知：
DF平分，
，
，
，
是外角的平分线，
，
，
，
，
，
，
，
是高，
，
，
的形状是等腰直角三角形．
故选：D．
根据画图过程可得：DF平分，，根据，得，由AM是外角的平分线，证得，得，进而证明的形状．
本题考查了作图基本作图、平行线的判定，等腰三角形的判定、等腰直角三角形，解决本题的关键是掌握画一个角的平分线的方法．
 

13.【答案】
 

【解析】解：由作法得，OP平分，则，
在和中
，
≌，
，
．
故答案为．
利用基本作图得到，OP平分，则，再证明≌得到，然后利用三角形外角性质计算．
本题考查了作图基本作图：作已知角的角平分线，还考查了三角形的外角性质、全等三角形的判定与性质 ．
 

14.【答案】
 

【解析】

【分析】
本题考查了作图基本作图：作已知角的角平分线，还考查了三角形的外角性质、全等三角形的判定与性质 ．
利用基本作图得到，OP平分，则，再证明≌得到，然后利用三角形外角性质计算．
【解答】
解：由作法得，OP平分，
则，
在和中
，
≌，
，
．
故答案为．  

15.【答案】
 

【解析】解：已知，求作射线OC，使OC平分：
步骤：a、在OA和OB上分别截取OD，OE，使；
b、分别以D，E为圆心，大于的长为半径作弧，在内，两弧交于C．
c、作射线OC；
故答案为．
根据作角平分线的步骤即可判断；
本题考查作图基本作图，解题的关键是熟练掌握作角平分线的步骤，属于中考常考题型．
 

16.【答案】
 

【解析】解：由作图可知：，
，
故答案为．
利用三角形的外角等于不相邻的两个内角的和即可解决问题．
本题考查作图基本作图，三角形的外角的性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
 

17.【答案】2
 

【解析】

【分析】
此题主要考查了基本作图以及全等三角形的判定与性质，正确得出E在的角平分线上是解题关键．根据题意得到，证明，进而得到答案．
【解答】
解：连接OE，作于点F，如图，

由题可知，，，，
，
，
点E到直线OB的距离是2．
故答案为2．  

18.【答案】解：如图所示：OC即为所求；

如图所示：OD即为所求；

如图所示：．
证明：
由作图可知，，，，
≌，
．
 

【解析】根据角平分线的作法作图即可；
根据过一点作已知直线的垂线的方法作图；
首先选定P点，再根据过一点作已知直线的垂线的方法作图，根据角平分线上的点到角两边的距离相等可得答案．
此题主要考查了复杂作图，关键是掌握角平分线的作法，过一点作已知直线的垂线的方法．
 

19.【答案】解：；
由基本作图方法可得：，，，
则在和中，
，
≌，
，
即OC为的平分线．
 

【解析】

【分析】
此题主要考查了应用设计与作图，正确掌握全等三角形的判定方法是解题关键．
直接利用角平分线的作法得出基本依据；
直接利用全等三角形的判定与性质得出答案．
【解答】
解：这种作已知角的平分线的方法的依据是．
故答案为：；
见答案．  

20.【答案】解：如图，BD为所作；

证明：，
，
平分，
，
，
，
为等腰三角形．
 

【解析】本题考查了基本作图：熟练掌握基本作图作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线也考查了等腰三角形的判定与性质．
利用基本作图作的平分线BD；
先利用等腰三角形的性质和三角形内角和计算出，再利用角平分线定义得到，接着根据三角形外角性质得到，然后根据等腰三角形的判定定理得到结论．
 

21.【答案】解：如图，射线AD即为所求．


证明：


平分



 

【解析】利用尺规作出的角平分线即可．
欲证明，只要证明即可．
本题考查作图基本作图，等腰三角形的判定，平行线的性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
 

22.【答案】解：BQ就是所求的的平分线，P、Q就是所求作的点．

证明：，
，
．
，
．
，
．
，
，
．

【解析】本题考查的是作图基本作图，熟知角平分线的作法和性质是解答此题的关键根据角平分线的性质作出BQ即可先根据垂直的定义得出，故再根据余角的定义得出，根据角平分线的性质得出，再由可知，据此可得出结论．
 

23.【答案】解：如图所示．

证明：，，，，
．
，分别是和的平分线，
，．
．
在和中，
．
．
在和中，
．
 

【解析】本题主要考查了基本作图和全等三角形的综合，关键是熟练掌握全等三角形的性质及判定方法．
利用角平分线的画法作图即可；
先证明，然后证明即可．