人教版新课标B必修12.1.4函数的奇偶性教案

这是一份人教版新课标B必修12.1.4函数的奇偶性教案，共13页。教案主要包含了教材，重点，教学法突破，过程分析，教学过程等内容，欢迎下载使用。


函数的奇偶性（教学设计）

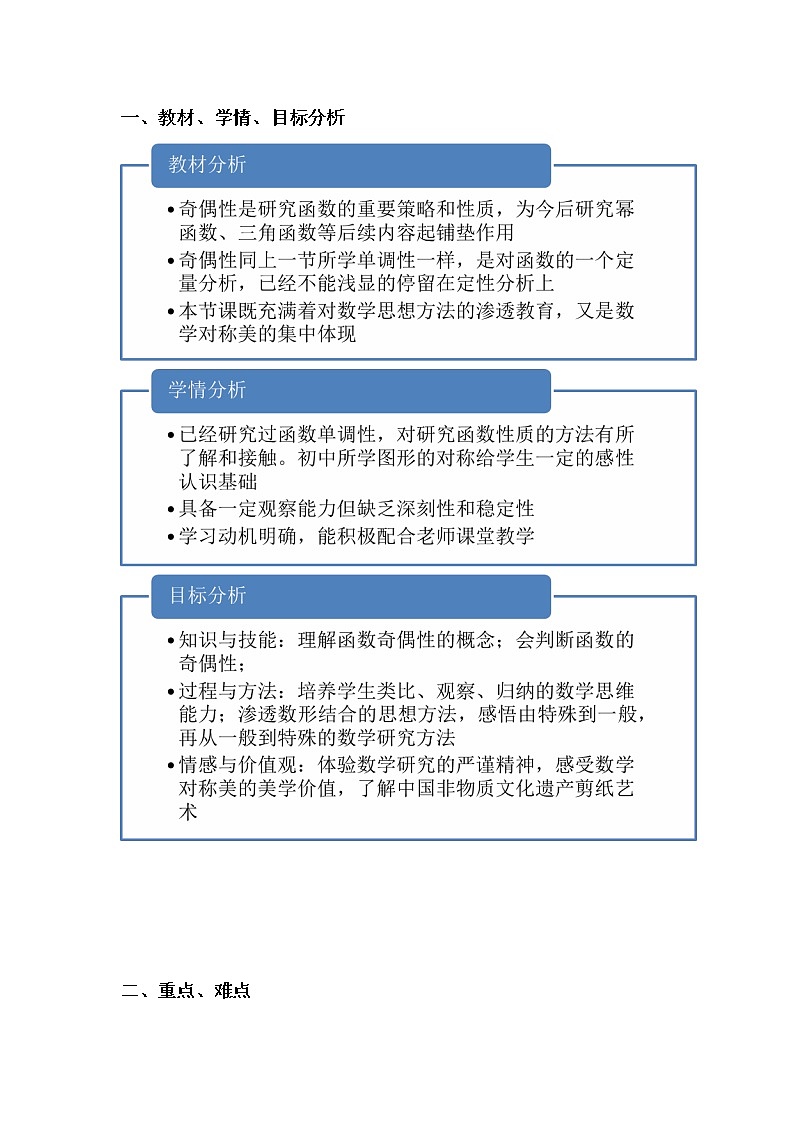
一、教材、学情、目标分析
二、重点、难点
三、教学法突破
四、过程分析
五、教学过程
（一）创设情境、引入课题
做一个剪纸的手工，对折后再剪出一个轴对称图形，让学生欣赏剪纸艺术大家的作品，了解这项非物质文化遗产，再给出生活中其他对称美的图片，让学生体会对称美，进而提出问题，
源于生活，那么我们现在正在学习的函数图象，是否也会具有对称的特性呢？是否也体现了图象对称的美感呢？
请同学们举出学过的体现对称美的图象。根据学生举得例子给出奇偶函数一个形象的定义，图象关于y轴对称的就是偶函数，关于原点对称的就是奇函数。然后设疑：怎么从数值上是去定义奇偶函数呢？
（二）设问诱导、讨论猜想
考察下面的函数：

☆思考1:根据形象认识可知这样的函数即为偶函数，那么这个函数的图象上的点的坐标有何特征呢？
☆思考2:对于上述两个函数，f(1)与f(-1)，f(2)与f(-2)，f(a)与f(-a)有什么关系？
几何画板展示：只要自变量互为相反数，函数值必相等。
一般地，若函数y=f(x)的图象关于y轴对称，当自变量x任取定义域中的一对相反数时，对应的函数值相等。 即 f(-x)=f(x)
☆思考3:怎样定义偶函数？（此处设置小组讨论，讨论2分钟，讨论闭又组长提出讨论的定义，教师板书）
☆思考4:函数 偶函数吗？偶函数的定义域有什么特征？（用此例帮助学生完善定义，若此前已完善，帮助学生强化定义中的软肋。）
练习1：判断下列函数是否为偶函数？（PPT展示，学生口答）
（三）合作探究、类比发现
仿照讨论偶函数的过程，回答下列问题，
共同完成探究

☆(1)请你仔细观察这两个函数图象，它们又有什么共同特征？
几何画板展示：只要自变量互为相反数，函数值必为相反数。
☆（2）类比偶函数定义，你能尝试利用数学语言描述函数图象的这个特征吗？
提问并板书奇函数的定义
练习2：判断下列函数是否为奇函数？（PPT展示，学生口答）
☆（3）给出一个复杂函数，但是定义域不对称，由此引出函数奇偶性的前提必是定义域关于原点对称。
（四）强化定义，深化内涵
☆对奇函数、偶函数定义的说明:
（1） 如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x) 具有奇偶性。
(2). 函数具有奇偶性的前提是：定义域关于原点对称。
练习3：奇函数定义域是[a,2a+3]，则a=_____.
进一步提出问题：判断正误并简要陈述理由
设函数y=f(x)的定义域为（-3,3），
1、满足f(-2)=f(2),f(-1)=f(1),则函数y=f(x)一定是偶函数（ ）
2、f(-2) ≠f(2) ，则函数y=f(x)一定不是偶函数（ ）
3、f(x)是偶函数则一定有f(-2)=f(2)（ ）
（注：此处设问是为了强调奇偶性的整体性。）
（四）讲练结合，巩固新知
例1. 利用定义判断下列函数的奇偶性
（1）
解：⑴先求定义域，看是否关于原点对称;否得非奇非偶函数；
⑵若是，再判断f(－x)与f(x)的关系；
(3)若f(-x)=f(x)则f(x)是偶函数;
若f(-x)= - f(x)则f(x)是奇函数.
否
是
将-x代入f（x），求f（-x）
相反数
相等
非奇非偶函数
☆ 小结：用定义判断函数奇偶性的步骤:
奇函数
偶函数
练习4.利用定义判断下列函数的奇偶性
（此处设置的练习囊括了奇、偶、既奇又偶、非奇非偶四种类型，既锻炼了学生判断奇偶性的能力，进一步为根据奇偶性分类做好铺垫。）
总结：根据奇偶性,
函数可划分为四类:
奇偶函数图象的性质:

注：奇偶函数图象的性质可用于：
①.判断函数的奇偶性； ②.简化函数图象的画法。
练习5：判断下列函数是否为偶函数或奇函数？（口答）
(1)
x
y
(2)
x
y
(4)
(3)
x
x
y
y
例2.已知函数y=f(x)是偶函数，它在y轴右边的图象如下图，画出在y轴左边的图象.
x
y
0
解：
相等en等
练习6：（1）已知函数y=f(x)是上的奇函数，它在上的图像如图所示，画出它在上的图像。
x
0
1
2
3
y
（五）拓展迁移，能力提高
例3. 利用定义判断下列函数的奇偶性
（1）
（2）
图象关于y轴对称
（六）课时小结，知识建构
图象关于原点对称
注意：若可以作出函数图象的，直接观察图象是否关于y轴对称或者关于原点对称。
（七）分层作业，回归拓展
层次一：学案课后作业A组；
层次二：学案课后作业B组；
层次三：补充题
（1）设f(x)是定义在R上的奇函数，当x>0时，f(x)=2x+1,求x<0时，f(x)的解析式.
（2）设f(x)是定义在R上的奇函数，当x>0时，f(x)=2x+1,求f(x)的解析式.
（八）板书设计