
_河南省周口市鹿邑县2020-2021学年九年级上学期期末数学试卷 (word版含答案)
展开2020-2021学年河南省周口市鹿邑县九年级(上)期末数学试卷
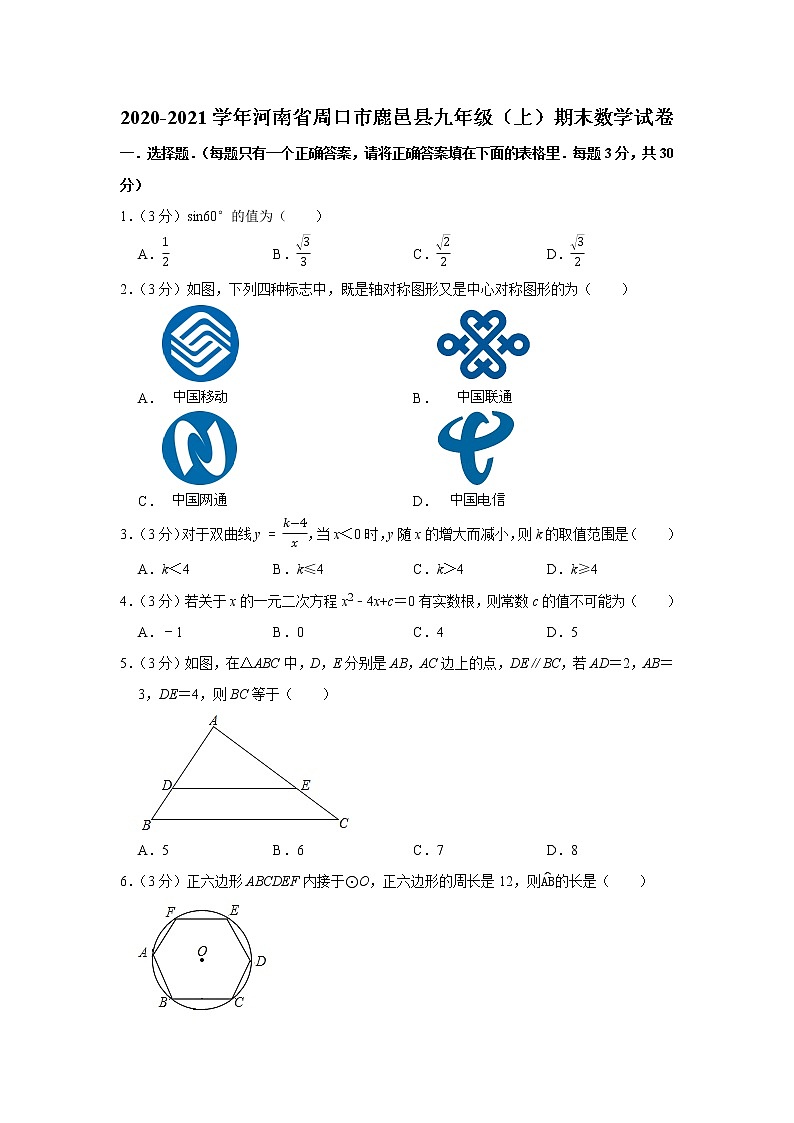
一.选择题.(每题只有一个正确答案,请将正确答案填在下面的表格里.每题3分,共30分)
1.(3分)sin60°的值为( )
A.12 B.33 C.22 D.32
2.(3分)如图,下列四种标志中,既是轴对称图形又是中心对称图形的为( )
A. B.
C. D.
3.(3分)对于双曲线y=k−4x,当x<0时,y随x的增大而减小,则k的取值范围是( )
A.k<4 B.k≤4 C.k>4 D.k≥4
4.(3分)若关于x的一元二次方程x2﹣4x+c=0有实数根,则常数c的值不可能为( )
A.﹣1 B.0 C.4 D.5
5.(3分)如图,在△ABC中,D,E分别是AB,AC边上的点,DE∥BC,若AD=2,AB=3,DE=4,则BC等于( )
A.5 B.6 C.7 D.8
6.(3分)正六边形ABCDEF内接于⊙O,正六边形的周长是12,则AB的长是( )
A.12π B.23π C.43π D.2π
7.(3分)如图,在▱ABCD中,点E在CD上,EC:DC=1:3,连接AE交BD于点F,则△DEF与△BAF的周长之比为( )
A.4:9 B.1:3 C.1:2 D.2:3
8.(3分)在反比例函数y=−2x图象上有三个点A(x1,y1)、B(x2,y2)、C(x3,y3),若x1<0<x2<x3,则下列结论正确的是( )
A.y3<y2<y1 B.y1<y3<y2 C.y2<y3<y1 D.y3<y1<y2
9.(3分)如图,A、B、C、D、E、G、H、M、N都是方格中的格点(即小正方形的顶点),要使△DEF与△ABC相似,则点F应是G、H、M、N中的( )
A.H或N B.G或H C.M或N D.G或M
10.(3分)二次函数y=ax2+bx+c的图象如图,现有以下结论:①abc>0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正确结论序号为( )
A.①③④ B.②③④ C.①②③ D.①②③④
二.填空题.(每题3分,共15分)
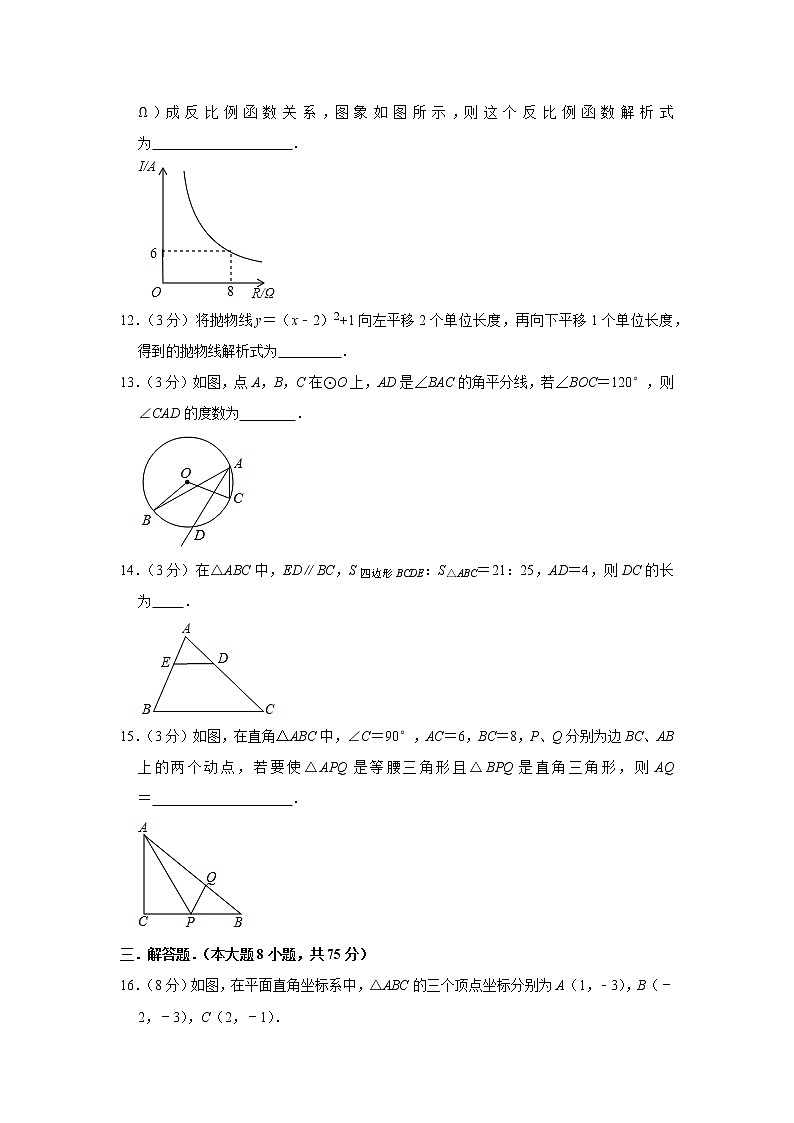
11.(3分)已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)成反比例函数关系,图象如图所示,则这个反比例函数解析式为 .
12.(3分)将抛物线y=(x﹣2)2+1向左平移2个单位长度,再向下平移1个单位长度,得到的抛物线解析式为 .
13.(3分)如图,点A,B,C在⊙O上,AD是∠BAC的角平分线,若∠BOC=120°,则∠CAD的度数为 .
14.(3分)在△ABC中,ED∥BC,S四边形BCDE:S△ABC=21:25,AD=4,则DC的长为 .
15.(3分)如图,在直角△ABC中,∠C=90°,AC=6,BC=8,P、Q分别为边BC、AB上的两个动点,若要使△APQ是等腰三角形且△BPQ是直角三角形,则AQ= .
三.解答题.(本大题8小题,共75分)
16.(8分)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,﹣3),B(﹣2,﹣3),C(2,﹣1).
(1)画出△ABC关于原点O成中心对称的△A1B1C1,并写出点C1的坐标;
(2)以原点O为位似中心,在x轴上方画出△ABC放大2倍后的△A2B2C2,并直接写出点C2的坐标.
17.(8分)甲、乙两所医院分别有一男一女共4名医护人员支援湖北武汉抗击疫情,从支援的4名医护人员中随机选2名,用列表或画树状图的方法求出这2名医护人员来自同一所医院的概率.
18.(8分)浮式起重机是海上打捞、海上救援和海上装卸的重要设备(如图①),某公司的浮式起重机需更换悬索,该公司设计了一个数学模型(如图②),测量知,∠A=30°,∠C=49°,AB=60m.请你利用以上数据,求出悬索AC和支架BC的长(结果取整数).参考数据:3≈1.73,sin49°≈0.75,cos49°≈0.66,tan49°≈1.15.
.
19.(9分)如图,△ABC中,D、E分别是AB、AC上的点,且BD=2AD,CE=2AE.
(1)求证:△ADE∽△ABC;
(2)若DF=2,求FC的长度.
20.(10分)如图,已知反比例函数y=k1x与一次函数y=k2x+b的图象交于点A(1,8),B(﹣4,m).
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积.
21.(10分)某公司经过市场调查,整理出某种商品在某个月的第x天与日销售量的相关信息如下表:
第x天
售价/(元/件)
日销售量/件
1≤x≤30
x+40
100﹣2x
已知商品的进价为20元/件,设该商品的日销售利润为y元.
(1)y与x的函数关系式为 ;
(2)在销售该商品的第几天时,日销售利润为2250元?
(3)当售价为多少元时,日销售利润最大?最大利润为多少?
22.(10分)如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作⊙O,与BC交于点M,与AB的另一个交点为E,过M作MN⊥AB,垂足为N.
(1)求证:MN是⊙O的切线;
(2)若⊙O的直径为5,sinB=35,求ED的长.
23.(12分)如图,已知抛物线y=−12x2+bx+c与x轴交于点A,点B(1,0),与y轴相交于点C(0,﹣2),直线AC经过点A、C.
(1)求抛物线和直线AC的解析式;
(2)若在直线AC上方的抛物线上有一点Q,使△AQC的面积最大,求出△AQC的最大面积并求出此时点Q的坐标;
(3)若点M是抛物线上一动点,过M作MN⊥x轴于点N,是否存在点M,使得以A、M、N为顶点的三角形与△AOC相似?若存在,请求出点M的坐标;若不存在,请说明理由.
2020-2021学年河南省周口市鹿邑县九年级(上)期末数学试卷
参考答案与试题解析
一.选择题.(每题只有一个正确答案,请将正确答案填在下面的表格里.每题3分,共30分)
1.(3分)sin60°的值为( )
A.12 B.33 C.22 D.32
【解答】解:sin60°=32,
故选:D.
2.(3分)如图,下列四种标志中,既是轴对称图形又是中心对称图形的为( )
A. B.
C. D.
【解答】解:A、不是轴对称图形,是中心对称图形,不符合题意;
B、既是轴对称图形,也是中心对称图形,符合题意;
C、不是轴对称图形,是中心对称图形,不符合题意;
D、不是轴对称图形,也不是中心对称图形,不符合题意.
故选:B.
3.(3分)对于双曲线y=k−4x,当x<0时,y随x的增大而减小,则k的取值范围是( )
A.k<4 B.k≤4 C.k>4 D.k≥4
【解答】解:∵双曲线y=k−4x,当x<0时,y随x的增大而减小,
∴k﹣4>0
∴k>4
故选:C.
4.(3分)若关于x的一元二次方程x2﹣4x+c=0有实数根,则常数c的值不可能为( )
A.﹣1 B.0 C.4 D.5
【解答】解:根据题意得Δ=(﹣4)2﹣4c≥0,
解得c≤4.
故选:D.
5.(3分)如图,在△ABC中,D,E分别是AB,AC边上的点,DE∥BC,若AD=2,AB=3,DE=4,则BC等于( )
A.5 B.6 C.7 D.8
【解答】解:∵DE∥BC,
∴△ADE∽△ABC,
∴ADAB=DEBC,
即23=4BC,
解得:BC=6,
故选:B.
6.(3分)正六边形ABCDEF内接于⊙O,正六边形的周长是12,则AB的长是( )
A.12π B.23π C.43π D.2π
【解答】解:连接OB,OA,
∵多边形ABCDEF是正六边形,
∴∠BOA=60°,
∵OB=OA,
∴△OBA是等边三角形,
∴OB=BA,
∵正六边形的周长是12,
∴BC=2,
∴⊙O的半径是2,
∴弧AB的长为60π×2180=2π3,
故选:B.
7.(3分)如图,在▱ABCD中,点E在CD上,EC:DC=1:3,连接AE交BD于点F,则△DEF与△BAF的周长之比为( )
A.4:9 B.1:3 C.1:2 D.2:3
【解答】解:∵四边形ABCD为平行四边形,
∴DC∥AB,
∴△DFE∽△BFA,
∵EC:DC=1:3,
∴DE:DC=2:3,
∴DE:AB=2:3,
∴C△DFE:C△BFA=2:3.
故选:D.
8.(3分)在反比例函数y=−2x图象上有三个点A(x1,y1)、B(x2,y2)、C(x3,y3),若x1<0<x2<x3,则下列结论正确的是( )
A.y3<y2<y1 B.y1<y3<y2 C.y2<y3<y1 D.y3<y1<y2
【解答】解:∵A(x1,y1)在反比例函数y=−2x图象上,x1<0,
∴y1>0,
对于反比例函数y=−2x,在第二象限,y随x的增大而增大,
∵0<x2<x3,
∴y2<y3<0,
∴y2<y3<y1
故选:C.
9.(3分)如图,A、B、C、D、E、G、H、M、N都是方格中的格点(即小正方形的顶点),要使△DEF与△ABC相似,则点F应是G、H、M、N中的( )
A.H或N B.G或H C.M或N D.G或M
【解答】解:设小正方形的边长为1,则△ABC的各边分别为3、13、10,只能F是M或N时,其各边是6、213,210.与△ABC各边对应成比例,
故选:C.
10.(3分)二次函数y=ax2+bx+c的图象如图,现有以下结论:①abc>0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正确结论序号为( )
A.①③④ B.②③④ C.①②③ D.①②③④
【解答】解:①由抛物线图象得:开口向下,即a<0;c>0,−b2a=−1<0,即b=2a<0,
∴abc>0,选项①正确;
②∵抛物线对称轴为x=﹣1,且x=0时,y>0,
∴当x=﹣2时,y=4a﹣2b+c>0,即4a+c>2b,选项②错误;
③∵抛物线对称轴x=﹣1,即−b2a=−1,
∴a=12b,
由图象可知,当x=1时,y=a+b+c=3b2+c<0,
故3b+2c<0,选项③正确;
④∵由图象可知,当x=﹣1时y取得最大值,
∵m≠﹣1,
∴am2+bm+c<a﹣b+c,即am2+bm+b<a,
∴m(am+b)+b<a,选项④正确;
故选:A.
二.填空题.(每题3分,共15分)
11.(3分)已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)成反比例函数关系,图象如图所示,则这个反比例函数解析式为 I=48R .
【解答】解:由图象经过(8,6),则IR=48,即I=48R.
故答案为:I=48R.
12.(3分)将抛物线y=(x﹣2)2+1向左平移2个单位长度,再向下平移1个单位长度,得到的抛物线解析式为 y=x2 .
【解答】解:将抛物线y=(x﹣2)2+1向左平移2个单位长度,再向下平移1个单位长度,得到的抛物线解析式为:y=(x﹣2+2)2+1﹣1,即y=x2.
故答案是:y=x2.
13.(3分)如图,点A,B,C在⊙O上,AD是∠BAC的角平分线,若∠BOC=120°,则∠CAD的度数为 30° .
【解答】解:∵∠BAC=12∠BOC=12×120°=60°,
而AD是∠BAC的角平分线,
∴∠CAD=12∠BAC=30°.
故答案为:30°.
14.(3分)在△ABC中,ED∥BC,S四边形BCDE:S△ABC=21:25,AD=4,则DC的长为 6 .
【解答】解:∵ED∥BC,
∴△AED∽△ABC,
∴ADAC=S△AEDS△ABC=25−2125=25,
∴AC=52AD=10,
∴DC=AC﹣AD=6.
故答案为:6.
15.(3分)如图,在直角△ABC中,∠C=90°,AC=6,BC=8,P、Q分别为边BC、AB上的两个动点,若要使△APQ是等腰三角形且△BPQ是直角三角形,则AQ= 154或307 .
【解答】解:①如图1中,当AQ=PQ,∠QPB=90°时,设AQ=PQ=x,
∵PQ∥AC,
∴△BPQ∽△BCA,
∴BQBA=PQAC,
∴10−x10=x6,
∴x=154,
∴AQ=154.
②当AQ=PQ,∠PQB=90°时,设AQ=PQ=y.
∵△BQP∽△BCA,
∴PQAC=BQBC,
∴y6=10−y8,
∴y=307.
综上所述,满足条件的AQ的值为154或307.
三.解答题.(本大题8小题,共75分)
16.(8分)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,﹣3),B(﹣2,﹣3),C(2,﹣1).
(1)画出△ABC关于原点O成中心对称的△A1B1C1,并写出点C1的坐标;
(2)以原点O为位似中心,在x轴上方画出△ABC放大2倍后的△A2B2C2,并直接写出点C2的坐标.
【解答】解:(1)如图,△A1B1C1,即为所求作.C1(﹣2,1).
(2)如图,△A2B2C2,即为所求作.C2(﹣4,2).
17.(8分)甲、乙两所医院分别有一男一女共4名医护人员支援湖北武汉抗击疫情,从支援的4名医护人员中随机选2名,用列表或画树状图的方法求出这2名医护人员来自同一所医院的概率.
【解答】解:将甲、乙两所医院的医护人员分别记为甲1、甲2、乙1、乙2(注:1表示男医护人员,2表示女医护人员),树状图如图所示:
由图可知,共12种等可能情况,其中符合条件的有4种,
∴这2名医护人员来自同一所医院的概率为412=13.
18.(8分)浮式起重机是海上打捞、海上救援和海上装卸的重要设备(如图①),某公司的浮式起重机需更换悬索,该公司设计了一个数学模型(如图②),测量知,∠A=30°,∠C=49°,AB=60m.请你利用以上数据,求出悬索AC和支架BC的长(结果取整数).参考数据:3≈1.73,sin49°≈0.75,cos49°≈0.66,tan49°≈1.15.
.
【解答】解:过点B作BD⊥AC于点D,
∵∠A=30°,AB=60,
∴BD=12AB=30,
∴AD=3BD=303,
在Rt△CBD中,
tan49°=BDCD,sin49°=BDBC,
∴CD≈26,BC≈40,
∴AC=AD+CD≈78.
19.(9分)如图,△ABC中,D、E分别是AB、AC上的点,且BD=2AD,CE=2AE.
(1)求证:△ADE∽△ABC;
(2)若DF=2,求FC的长度.
【解答】(1)证明:∵BD=2AD,CE=2AE,
∴ADAB=AEAC=13,
又∵∠DAE=∠BAC,
∴△ADE∽△ABC;
(2)解:∵△ADE∽△ABC,
∴DEBC=ADAB=13,∠ADE=∠ABC,
∴DE∥BC,
∴△DEF∽△CBF,
∴DFCF=DECB,即2CF=13,
∴FC=6.
20.(10分)如图,已知反比例函数y=k1x与一次函数y=k2x+b的图象交于点A(1,8),B(﹣4,m).
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积.
【解答】解:(1)点A(1,8)在反比例函数y=k1x的图像上,
代入得:k1=8,
∴反比例函数的解析式为y=8x,
将B(﹣4,m)代入y=8x,得:m=﹣2,
∴点B(﹣4,﹣2),
将A(1,8),B(﹣4,﹣2)代入y=k2x+b得,
k2+b=8,﹣4k2+b=﹣2,
解得k2=2,b=6,
∴一次函数的解析式为y=2x+6;
(2)当x=0时,y=6,
∴一次函数与与y轴的交点坐标为(0,6),
∴S△AOB=12×4×6+12×1×6=15,
答:△AOB的面积是15.
21.(10分)某公司经过市场调查,整理出某种商品在某个月的第x天与日销售量的相关信息如下表:
第x天
售价/(元/件)
日销售量/件
1≤x≤30
x+40
100﹣2x
已知商品的进价为20元/件,设该商品的日销售利润为y元.
(1)y与x的函数关系式为 y=﹣2x2+60x+2000 ;
(2)在销售该商品的第几天时,日销售利润为2250元?
(3)当售价为多少元时,日销售利润最大?最大利润为多少?
【解答】解:(1)根据题意,得y=(100﹣2x)(x+40﹣20),
即y=﹣2x2+60x+2000;
故答案为:y=﹣2x2+60x+2000;
(2)依题意得:﹣2x2+60x+2000=2250,
整理得:x2﹣30x+125=0,
解:x1=25,x2=5,
即第5天或第25天时,日销售利润为2250元;
(3)由y=﹣2x2+60x+2000=﹣2(x﹣15)2+2450,
即当x=15时,日销售利润有最大值为2450元,
此时,售价应为15+40=55元.
答:当售价为55元时,日销售利润最大,最大利润为2450.
22.(10分)如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作⊙O,与BC交于点M,与AB的另一个交点为E,过M作MN⊥AB,垂足为N.
(1)求证:MN是⊙O的切线;
(2)若⊙O的直径为5,sinB=35,求ED的长.
【解答】(1)证明:连接OM,如图1,
∵OC=OM,
∴∠OCM=∠OMC,
在Rt△ABC中,CD是斜边AB上的中线,
∴CD=12AB=BD,
∴∠DCB=∠DBC,
∴∠OMC=∠DBC,
∴OM∥BD,
∵MN⊥BD,
∴OM⊥MN,
∵OM过O,
∴MN是⊙O的切线;
(2)解:连接DM,CE,
∵CD是⊙O的直径,
∴∠CED=90°,∠DMC=90°,
即DM⊥BC,CE⊥AB,
由(1)知:BD=CD=5,
∴M为BC的中点,
∵sinB=35,
∴cosB=45,
在Rt△BMD中,BM=BD•cosB=4,
∴BC=2BM=8,
在Rt△CEB中,BE=BC•cosB=325,
∴ED=BE﹣BD=325−5=75.
23.(12分)如图,已知抛物线y=−12x2+bx+c与x轴交于点A,点B(1,0),与y轴相交于点C(0,﹣2),直线AC经过点A、C.
(1)求抛物线和直线AC的解析式;
(2)若在直线AC上方的抛物线上有一点Q,使△AQC的面积最大,求出△AQC的最大面积并求出此时点Q的坐标;
(3)若点M是抛物线上一动点,过M作MN⊥x轴于点N,是否存在点M,使得以A、M、N为顶点的三角形与△AOC相似?若存在,请求出点M的坐标;若不存在,请说明理由.
【解答】解:(1)将B(1,0)、C(0,﹣2)代入y=−12x2+bx+c中得:b=52,c=−2,
∴y=−12x2+52x−2,
∴该抛物线的对称轴为x=52,
∵B(1,0),
∴A(4,0),
令直线AC的解析式为y=kx+b,将A(4,0),C(0,﹣2),
代入得:k=12,b=−2,
∴y=12x−2,
(2)令Q(m,−12m2+52m−2),连接OQ,
则S△AOQ=12|yQ|⋅OA=12×4(−12m2+52m−2),S△AOC=12OA⋅OC=12×4×2=4,
∴S四边形OCAQ=S△AOC+S△AOQ=−m2+5m−4+4=−m2+5m,
∵S△AQC=S四边形△OCAQ=−m2+5m−12×2×m=−m2+4m=﹣(m﹣2)2+4,
∵﹣1<0,
∴m=2时,△AQC的面积最大为4,
此时Q(2,1),
(3)存在点M使以A,M,N为顶点的三角形与△OAC相似,
设M(a,−12a2+52a−2),则N(a,0),分两种情况,
①若△NMA∽△OAC,则MNOA=ANOC,
即|−12a2+52a−2|4=|4−a|2,
则|16﹣4a|=|a2﹣5a+4|,
当a2﹣5a+4=16﹣4a时,得a1=4(舍),a2=﹣3,
当a2﹣5a+4=4a﹣16时,a1=5,a2=4(舍),
即M1(﹣3,﹣14),M2(5,﹣2),
②若△NAM∽△OAC,则MNOC=ANOA,
即|−12a2+52a−2|2=|4−a|4,
则|2a2﹣10a+8|=|8﹣2a|,
当2a2﹣10a+8=8﹣2a时,a1=0,a2=4(舍),即M3(0,﹣2),
当2a2﹣10a+8=2a﹣8时,a1=2,a2=4(舍),即M4(2,1),
综上所述,M1(﹣3,﹣14),M2(5,﹣2),M3(0,﹣2),M4(2,1).
河南省周口市鹿邑县2022-2023学年七年级上学期学习评价数学试卷(一)(含答案): 这是一份河南省周口市鹿邑县2022-2023学年七年级上学期学习评价数学试卷(一)(含答案),共16页。试卷主要包含了的绝对值是,计算的结果是,如下表,下列各式不成立的是等内容,欢迎下载使用。
河南省周口市鹿邑县2021-2022学年七年级下学期期中数学试题(word版含答案): 这是一份河南省周口市鹿邑县2021-2022学年七年级下学期期中数学试题(word版含答案),共7页。试卷主要包含了选择题.,填空题.,解答题.等内容,欢迎下载使用。
河南省周口市鹿邑县2020-2021学年七年级上学期期末考试数学试题(图片版): 这是一份河南省周口市鹿邑县2020-2021学年七年级上学期期末考试数学试题(图片版),文件包含河南省周口市鹿邑县2020-2021学年七年级上学期期末考试数102601pdf、河南省周口市鹿邑县2020-2021学年七年级上学期期末考试数102601答案pdf等2份试卷配套教学资源,其中试卷共4页, 欢迎下载使用。












