





高中数学苏教版必修12.2.1 函数的单调性集体备课ppt课件
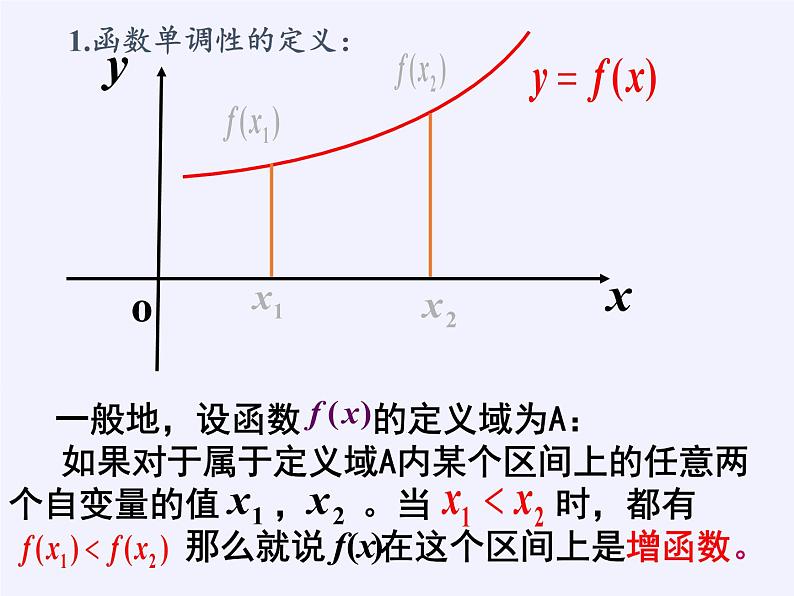
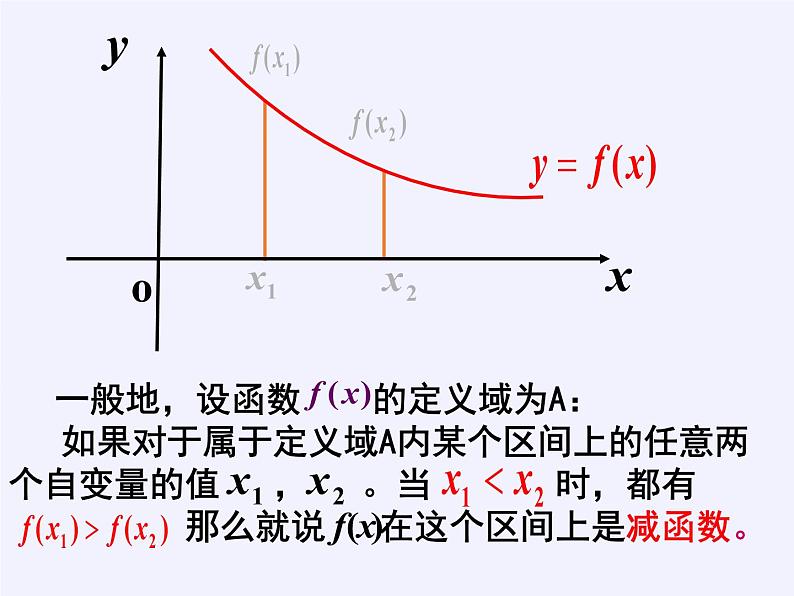
展开1.函数单调性的定义:
注: ①函数的单调区间只能是其定义域的子区间;
②必须是对于区间D内的任意两个自变量x1,x2;当 x1
③函数的单调区间是连续区间, 若区间不连续, 应分段考查.
④在单调区间上, 增函数的图象自左向右看是上升的, 减函数的图象自左向右看是下降的.
2. 证明函数单调性的一般方法:
1.定义法: 设 , 作差(一般结果要分解为若干个因式的积或商,且每一个因式的正或负号能清楚地判断出);判断正负号.(若差为负值则为增函数;反之则为减函数)。做商法也行,最后判断商与“1”的大小.
注:函数 f(x) 在区间 D 上单调递增(或递减): 不等式 f (x)≥0(≤0) 对于 xD 恒成立.
3.求单调区间的方法: 定义法、导数法、图象法、利用已知函数的单调性 4.一些有用的结论:
一次函数 y=kx+b(k≠0)反比例函数二次函数 y=ax2+bx+c(a≠0)指数函数 y=ax(a>0,a≠1) 对数函数 y=lgax(a>0,a≠1)
5.利用函数的运算性质判断函数的单调性.
若f(x), g(x)为增函数,则在其公共定义域上有:
y=f(x)+g(x)为增函数.
y=-f(x) 为减函数.
一次函数 y=kx+b(k≠0) 当k>0时,(-∞,+∞)是这个函数的单调增区间; 当k<0时,(-∞,+∞)是这个函数的单调减区间.
当k>0时,(-∞,0)和(0,+∞)都是这个函数的单调减区间; 当k<0时,(-∞,0)和(0,+∞)都是这个函数的单调增区间.
二次函数y=ax2+bx+c(a≠0) 当a>0时, 是这个函数的单调减区间, 是它的单调增区间; 当a<0时, 是这个函数的单调增区间, 是它的单调减区间;
指数函数y=ax(a>0,a≠1). 当a>1时, (-∞,+∞) 是这个函数的单调增区间; 当0<a<1时,(-∞,+∞)是这个函数的单调减区间.
对数函数y=lgax(a>0,a≠1). 当a>1时,(0,+∞)是这个函数的单调增区间; 当0<a<1时,(0,+∞)是它的单调减区间.
奇函数在其定义域的对称区间上单调性相同, 偶函数在其定义域的对称区间上单调性相反;
二、基础训练
1、函数y=2x+1在 单调递 ,函数y=-x2-2x-1的单调增区间为 函数y=x+ 的单调减区间为 ,2、函数y= 的单调 区间为 3、函数 在 上是减函数,则实数a 的取值范围是
例1、证明函数f(x)=x2+ 在(1,+∞)上递增
四、回顾小结:
1. 讨论函数单调性必须在其定义域内进行,因此要研究函数单调性必须先求函数的定义域,函数的单调区间是定义域的子集;
2.判断函数的单调性的方法有:(1)用定义;(2)用已知函数的单调性;(3)利用函数的导数.
谢谢各位专家的光临指导
高中数学苏教版必修12.2.1 函数的单调性评课课件ppt: 这是一份高中数学苏教版必修12.2.1 函数的单调性评课课件ppt,共27页。PPT课件主要包含了逐渐上升,逐渐下降,增函数,减函数,区间D,单调区间的定义,答案D,考点探究,悟法1,练习1等内容,欢迎下载使用。
高中数学苏教版必修1第2章 函数2.2 函数的简单性质2.2.1 函数的单调性图片课件ppt: 这是一份高中数学苏教版必修1第2章 函数2.2 函数的简单性质2.2.1 函数的单调性图片课件ppt,共29页。PPT课件主要包含了课前准备,反思与疑问等内容,欢迎下载使用。
高中数学苏教版必修1第2章 函数2.2 函数的简单性质2.2.1 函数的单调性教课内容课件ppt: 这是一份高中数学苏教版必修1第2章 函数2.2 函数的简单性质2.2.1 函数的单调性教课内容课件ppt,共29页。PPT课件主要包含了单调增区间,单调减区间,单调性,单调区间,fx≤fx0,规律方法总结,高考真题,全解密等内容,欢迎下载使用。













