苏教版必修12.2.1 函数的单调性课文内容课件ppt

这是一份苏教版必修12.2.1 函数的单调性课文内容课件ppt，共15页。PPT课件主要包含了x12，x22，某个区间D，逗号隔开，用“和”连接，例2利用定义证明，作差变形，判断差符号，下结论等内容，欢迎下载使用。

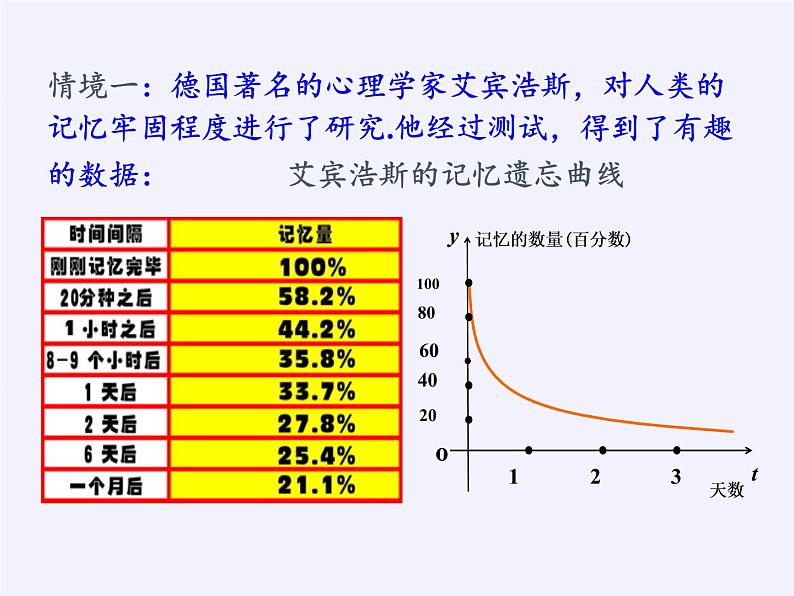
情境一：德国著名的心理学家艾宾浩斯，对人类的记忆牢固程度进行了研究.他经过测试，得到了有趣的数据： 艾宾浩斯的记忆遗忘曲线
情境二：南通某学校派一小组学生到青海湿地进行调研考察，下图是该市当日24小时内的气温变化图，你能说出这一天的气温变化趋势吗？
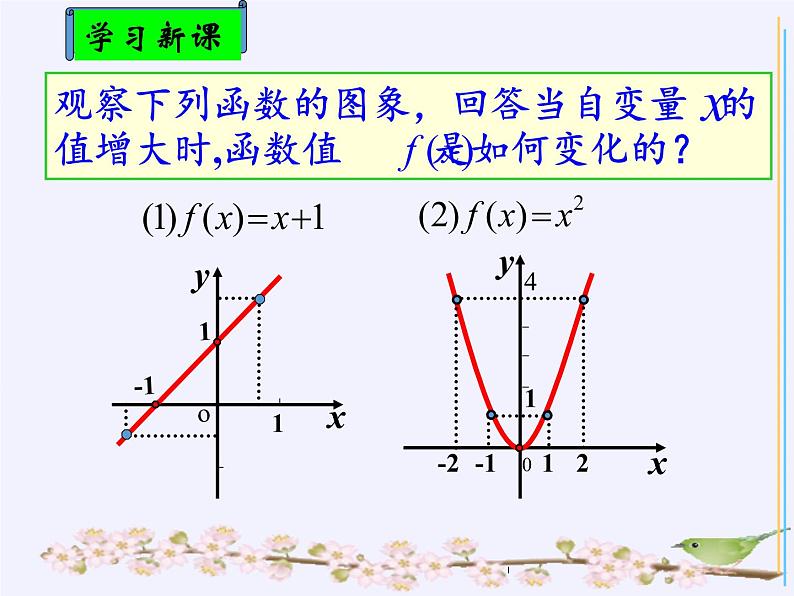
观察下列函数的图象，回答当自变量 的值增大时,函数值 是如何变化的？
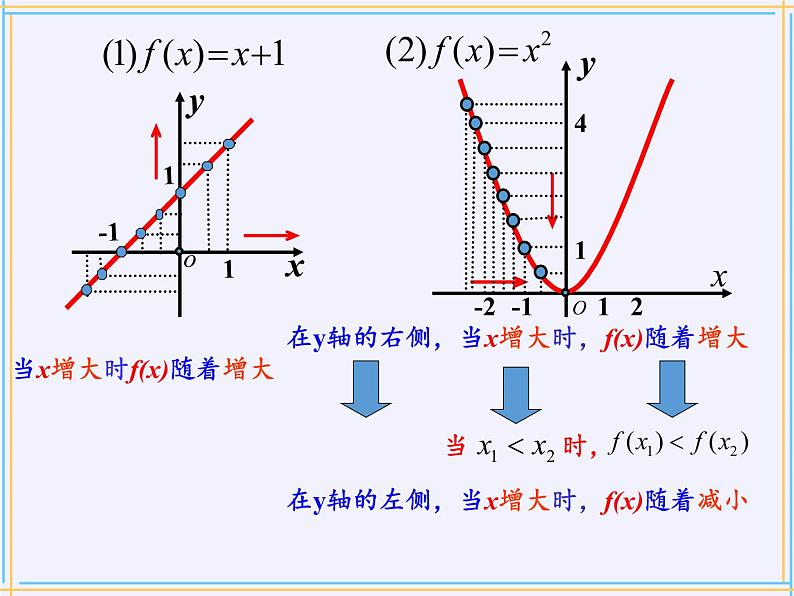
在y轴的左侧，当x增大时，f(x)随着减小
当x增大时f(x)随着增大
在y轴的右侧，当x增大时，f(x)随着增大
 函数 f(x)=x2 :
在(0,+∞)上任取 x1、x2 ,
如果对于定义域I内某个区间D上的任意两个自变量的值 x1 、x2 ，当 x1＜x2时，都有f(x1)＜f(x2)，那么就说函数f(x)在区间D上是增函数.
一般地，设函数 f(x)的定义域为I:
如果对于定义域I内某个区间D上的任意两个自变量的值 x1 、x2 ，当 x1＜x2时，都有f(x1)＞f(x2)，那么就说函数f(x)在区间D上是减函数.
如果函数y=f(x)在区间D上是增函数或减函数，那么就说函数y=f(x)在这一区间上具有(严格的)单调性，区间D叫做函数f(x)的单调区间.
解:函数y=f(x)的单调区间有[－5,－2）,[－2,1) ，[1，3), [3，5].
例1. 如图是定义在闭区间[－5,5]上的函数 y = f(x)的图象, 根据图象说出函数的单调区间, 以及在每一单调区间上, 函数是增函数还是减函数？
其中y=f(x)在区间[－2，1)，[3，5]上是增函数；
说明:孤立的点没有单调性,故区间端点处若有定义写开写闭均可.
函数　　　 在 上是减函数.
5.下结论:由定义得出函数的单调性.
1.设值:设任意x1、x2属于给定区间,且x1< x2
2.作差:作差f(x1)-f(x2) ；
4.判号:确定f(x1)-f(x2)的正负；
证明函数单调性的步骤：
3.变形:对f(x1)-f(x2)适当变形；
证明函数　 在区间(0,+∞)上是增函数
证:设 是(0,+∞)上任意两个值且
在区间(0,+∞)上是增函数．
3.(定义法)证明函数单调性的步骤:
2.图象法判断函数的单调性：
1. 增函数、减函数的定义；
1、必做题:课本39页A组第1、2题
2、选做题:由生活常识都知道，在一碗糖水中，加入一定量的糖，糖加得越多糖水就越甜．你能运用今天所学的数学知识来解说这一现象吗？