




初中数学2.5 全等三角形背景图ppt课件
展开这是一份初中数学2.5 全等三角形背景图ppt课件,共17页。PPT课件主要包含了全等三角形的性质,ABAD已知,ACAE已知,AOBO已知,∠A∠B已知,∠A∠C已证,∠B∠D已知,ABCD已知,归纳总结等内容,欢迎下载使用。
全等三角形的对应边相等, 对应角相等。
全等三角形判定方法1.
在两个三角形中,如果有两条边及它们的夹角对应相等,那么这两个三角形全等(边角边)(简记为SAS)
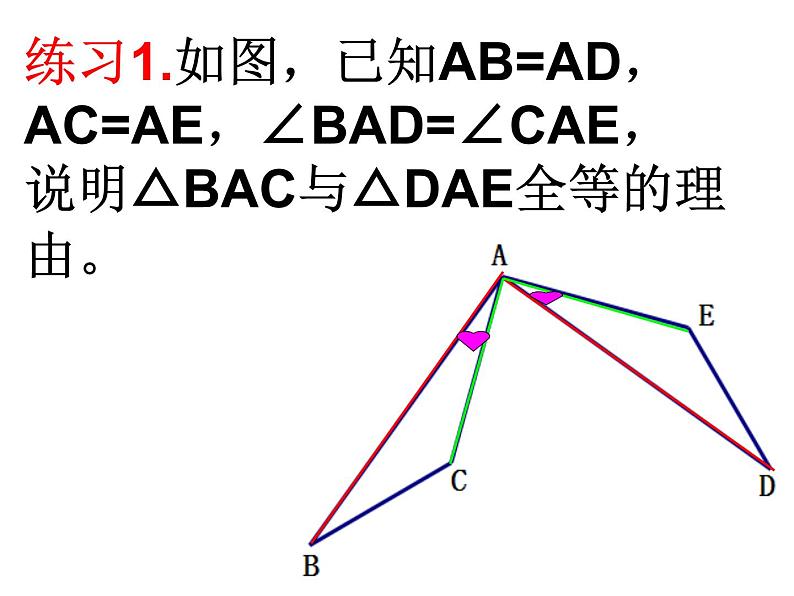
练习1.如图,已知AB=AD,AC=AE,∠BAD=∠CAE, 说明△BAC与△DAE全等的理由。
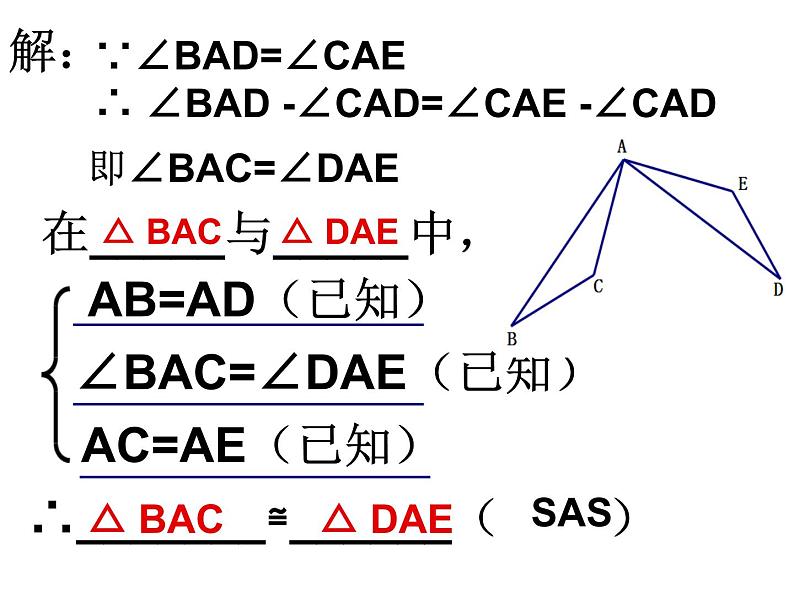
在_____与_____中,
∠BAC=∠DAE(已知)
∴_______≌______( )
∵∠BAD=∠CAE∴ ∠BAD -∠CAD=∠CAE -∠CAD
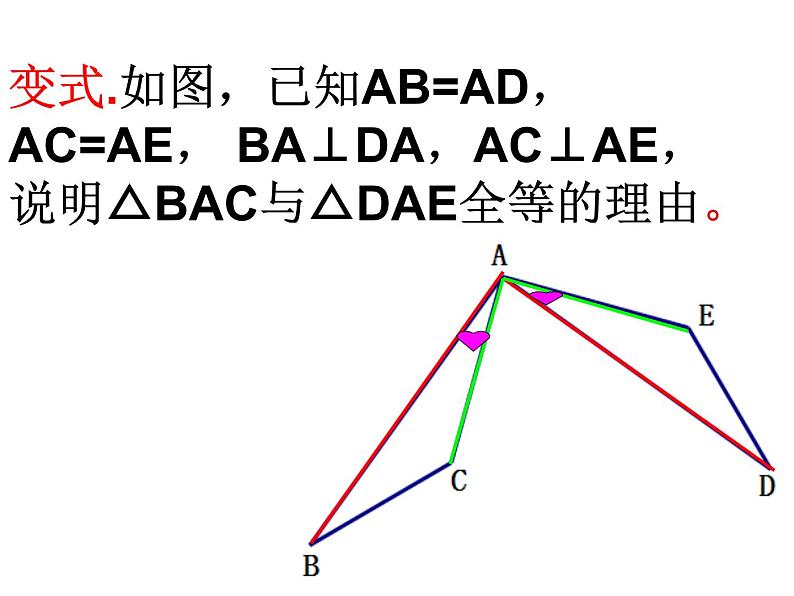
变式.如图,已知AB=AD,AC=AE, BA⊥DA,AC⊥AE, 说明△BAC与△DAE全等的理由。
如图,△ABC与△DEF中,已知BC=EF,∠B=∠E, ∠C=∠F。那么△ABC≌△DEF
全等三角形判定方法2.
在两个三角形中,如果有两个角及它们的夹边对应相等,那么这两个三角形全等.
(称为角边角)(简记为ASA)
例题1.如图,已知AB与CD相交于点O,AO=BO,∠B=∠A, 说明△AOC与△BOD全等的理由。
在△ AOC与△ BOD中,
∠AOC=∠BOD(对顶角相等)
∴△ AOC≌△ BOD(ASA)
拓展1:如图,已知AB与CD相交于点O,AO=BO,∠B=∠A, 试判断CO与DO的关系。
拓展2:如图,已知AB与CD相交于点O,AO=BO,AC∥BD, 求证: AC=BD 。
例题2.如图,点A、F、E、C在同一直线 上,AB∥DC, AB=CD ∠B=∠D, 求证:△ABE≌△CDF
∴△ ABE≌△ CDF(ASA)
在△ ABE与△ CDF中,
(两直线平行,内错角相等)
1、全等三角形的判定定理1(边角边定理)2、全等三角形的判定定理2(角边角定理)3、用途:
在两个三角形中,如果有两条边及它们的夹角对应相等,那么这两个三角形全等(简记为“边角边”或“SAS ” )
在两个三角形中,如果有两个角及它们的夹边对应相等,那么这两个三角形全等.(简记为“角边角”或“ASA ” )
证明三角形全等通过证明三角形全等证明两个三角形中的线段相等或角相等。
1.已知点D 在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B= ∠C(如图),求证:BE=CD.
相关课件
这是一份初中数学湘教版八年级上册第2章 三角形2.5 全等三角形教学ppt课件,文件包含教学课件八上·湘教·25全等三角形第3课时全等三角形的判定ASApptx、253docx等2份课件配套教学资源,其中PPT共17页, 欢迎下载使用。
这是一份数学八年级上册2.5 全等三角形说课课件ppt,文件包含湘教版数学八年级上册-25第2课时全等三角形的判定SASppt、湘教版数学八年级上册-25第2课时全等三角形的判定SASdocx等2份课件配套教学资源,其中PPT共0页, 欢迎下载使用。
这是一份2020-2021学年2.5 全等三角形课文配套ppt课件,共21页。PPT课件主要包含了帮帮我,∠C∠D,AAS,知识应用,练一练,知识要点等内容,欢迎下载使用。













