2021年人教A版必修2数学第1章_空间几何体单元测试卷含答案

这是一份2021年人教A版必修2数学第1章_空间几何体单元测试卷含答案，共17页。试卷主要包含了 选择题， 填空题， 解答题等内容，欢迎下载使用。

一、 选择题 （本题共计 12 小题 ，每题 5 分 ，共计60分 ， ）

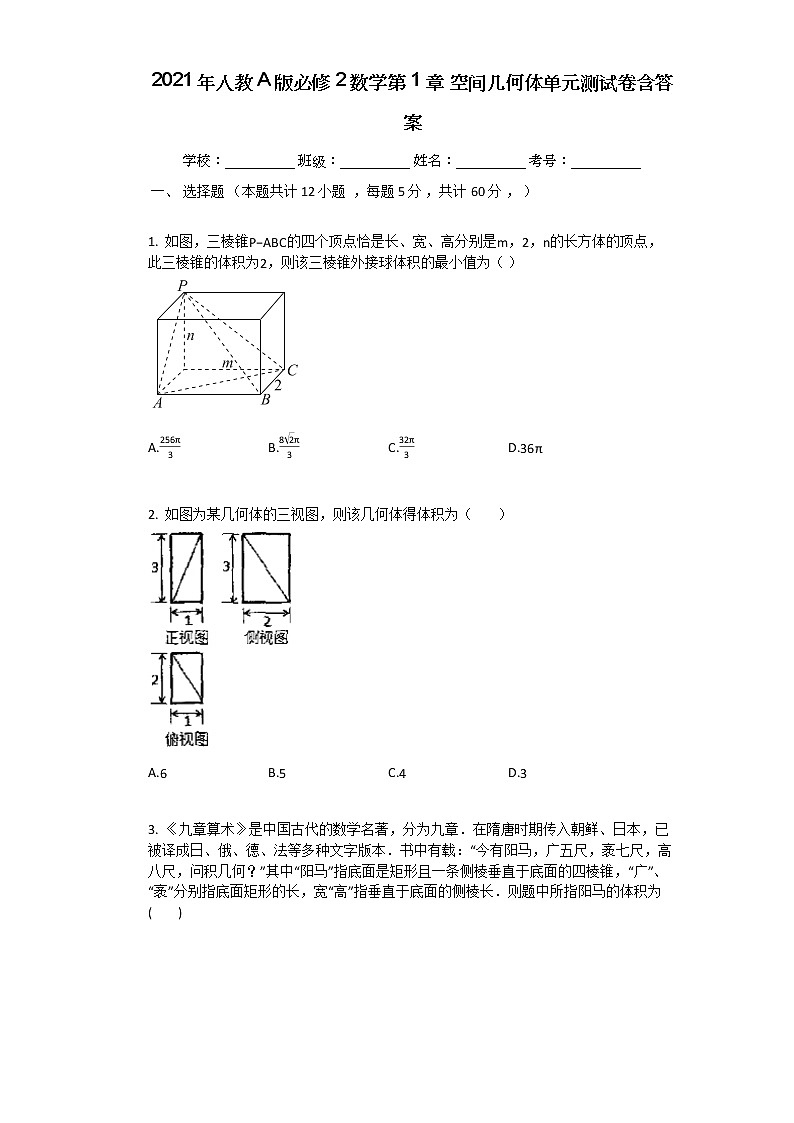
1. 如图，三棱锥P−ABC的四个顶点恰是长、宽、高分别是m，2，n的长方体的顶点，此三棱锥的体积为2，则该三棱锥外接球体积的最小值为（ ）

A.256π3B.82π3C.32π3D.36π

2. 如图为某几何体的三视图，则该几何体得体积为（ ）

A.6B.5C.4D.3

3. 《九章算术》是中国古代的数学名著，分为九章．在隋唐时期传入朝鲜、日本，已被译成日、俄、德、法等多种文字版本．书中有载：“今有阳马，广五尺，袤七尺，高八尺，问积几何？”其中“阳马”指底面是矩形且一条侧棱垂直于底面的四棱锥，“广”、“袤”分别指底面矩形的长，宽“高”指垂直于底面的侧棱长．则题中所指阳马的体积为( )

A.1403立方尺B.2803立方尺C.140立方尺D.280立方尺

4. 如图所示，观察四个几何体，其中判断正确的是（ ）

A.(1)是棱台B.(2)是圆台C.(3)是棱锥D.(4)不是棱柱

5. 如图，一个空间几何体的三视图都是半径为2的圆，则这个几何体的表面积为( )

A.4πB.8π C.12πD.16π

6. 已知圆锥的表面积为9π，且它的侧面展开图是一个半圆，则这个圆锥的底面半径为( )
A.3B.3C.23D.33

7. 由几块大小相同的正方体搭成如图所示的几何体，它的侧视图是（ ）

A.B.C.D.

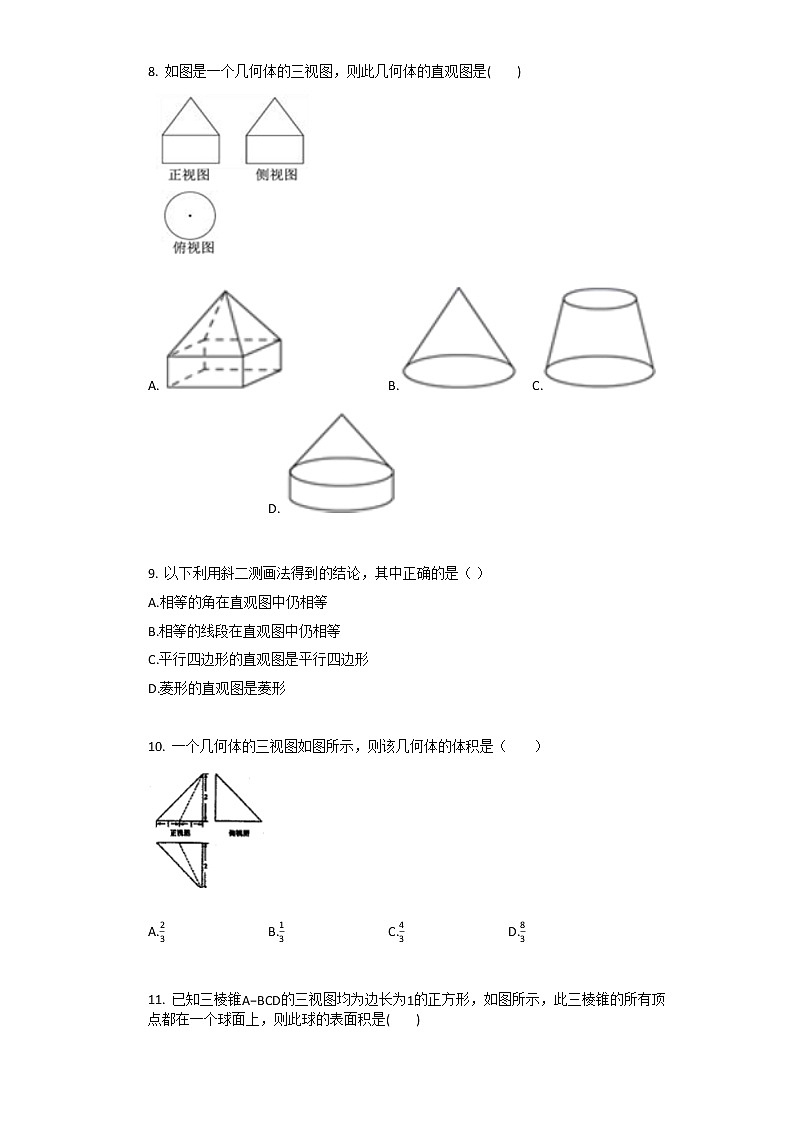
8. 如图是一个几何体的三视图，则此几何体的直观图是( )

A.B.C.D.

9. 以下利用斜二测画法得到的结论，其中正确的是（ ）
A.相等的角在直观图中仍相等
B.相等的线段在直观图中仍相等
C.平行四边形的直观图是平行四边形
D.菱形的直观图是菱形

10. 一个几何体的三视图如图所示，则该几何体的体积是（ ）

A.23B.13C.43D.83

11. 已知三棱锥A−BCD的三视图均为边长为1的正方形，如图所示，此三棱锥的所有顶点都在一个球面上，则此球的表面积是( )

A.π3B.2π3C.3πD.π4

12. 摩索拉斯陵墓位于哈利卡纳素斯，在土耳其（TURKEY）的西南方，陵墓由下至上分别是墩座墙、柱子构成的拱廊、四棱锥金字塔以及由四匹马拉着的一架古代战车的雕像，总高度45米，其中墩座墙和柱子围成长、宽、高分别是40米、30米、32米的长方体，长方体的上底面与四棱锥的底面重合，顶点在底面的射影是长方形对角线交点，最顶部的马车雕像高6米，则陵墓的高与金字塔的侧棱长之比大约为（ ）（注：674≈25.962）

二、 填空题 （本题共计 4 小题 ，每题 5 分 ，共计20分 ， ）

13. 如图，圆柱OO′的底面半径为2cm，高为4cm，且P为母线B′B的重点，∠AOB=120∘，则一蚂蚁从A点沿圆柱表面爬到P点的最短路程为________


14. 圆锥的底面半径为3，高是4，在这个圆锥内部有一个内切球，则此内切球的半径为________.

15. 如图已知梯形ABCD的直观图A′B′C′D′的面积为10，则梯形ABCD的面积为________．


16. 已知一个圆锥的侧面积为6π，它的侧面展开图是一个半圆，则此圆锥的体积为________.
三、 解答题 （本题共计 6 小题 ，每题 11 分 ，共计66分 ， ）

17. 若一个圆台的母线长为10cm，高为8cm，下底面面积为64πcm2，请求出截得此圆台的圆锥的母线长是多少．

18. 画底面边长为2cm、高为3cm的正四棱柱ABCD−A1B1C1D1的直观图．

19. 我国古代《九章算术》中将上，下两面为平行矩形的六面体称为刍童．
(1)如果一个长方体ABCD−A1B1C1D1长宽高分别是3、4、5，可以看成一个特殊的刍童，请指出它的外接球的球心的位置，并求出外接球表面积；

(2)如图的刍童ABCD−EFGH有外接球，且AB=27，AD=2，EH=23，EF=22，平面ABCD与平面EFGH间的距离为1，求该刍童外接球的体积．

20. 已知一个几何体的三视图如图，试求它的表面积和体积．（单位：cm）


21. 一个几何体的三视图如下图所示（单位：m），

(1)该几何体是由哪些简单几何体组成的；

(2)求该几何体的表面积和体积．

22. 已知某几何体的俯视图是如图所示的矩形，正视图是一个底边长为8、高为2的等腰三角形，侧视图是一个底边长为6、高为2的等腰三角形．

(1)求该几何体的表面积S；

(2)求该几何体的体积V．
参考答案与试题解析
2021年人教A版必修2数学第1章 空间几何体单元测试卷含答案
一、 选择题 （本题共计 12 小题 ，每题 5 分 ，共计60分 ）
1.
【答案】
C
【考点】
球的表面积和体积
球内接多面体
【解析】
外接球的半径与长方体的棱长的关系求出半径的最小值，进而求出外接球的最小值．
【解答】
由题意知V锥=13⋅12⋅m⋅n⋅2＝2，所以mn＝6，设外接球的半径为R，则2R=m2+n2+4≥2mn+4=4，∴ R≥2，
所以外接球的体积V=4π3R3≥32π3，
2.
【答案】
BC
【考点】
由三视图求体积
【解析】
此题暂无解析
【解答】
此题暂无解答
3.
【答案】
B
【考点】
柱体、锥体、台体的体积计算
【解析】
利用棱锥的体积公式直接求即可．
【解答】
解：根据题意，阳马体积为V=13×5×7×8=2803立方尺．
故选B．
4.
【答案】
C
【考点】
旋转体（圆柱、圆锥、圆台）
棱锥的结构特征
棱柱的结构特征
棱台的结构特征
【解析】
利用棱锥，棱柱，棱台，圆台的定义，判断即可.
【解答】
解：棱台可以看作是圆锥，用平行底面的截面截去一个棱锥的剩余部分，所以(1)不是棱台；
(2)的几何体的上下两个底面不平行，所以(2)不是圆台；
(3)是棱锥，所以C的判断正确；
(4)是棱柱，左右两个面是棱柱的一个底面，所以D不正确.
故选C．
5.
【答案】
D
【考点】
由三视图求表面积
【解析】
根据已知中的三视图，我们可以判断出该几何体的形状是球，利用球的表面积公式，即可得到该几何体的表面积．
【解答】
解：由三视图可知，该几何体是半径为2的球体,
则该几何体的表面积为S=4π×22=16π.
故选D.
6.
【答案】
B
【考点】
旋转体（圆柱、圆锥、圆台）
【解析】
此题暂无解析
【解答】
解：设圆锥的底面半径为r，由于圆锥侧面展开图是一个半圆，
故其母线长为2πrπ=2r，
所以圆锥的表面积为πr2+12π2r2=9π，解得r=3.
故选B.
7.
【答案】
D
【考点】
简单空间图形的三视图
【解析】
由图知，侧视图有2列，每列小正方形的数目分别为1，2，依据这些特点，可得它的侧视图．
【解答】
解：由图知，侧视图有2列，每列小正方形的数目分别为1，2，
从而可知它的侧视图是．
故选：D．
8.
【答案】
D
【考点】
由三视图还原实物图
【解析】
此题暂无解析
【解答】
解：由该几何体的三视图可知，该几何体是由一个圆锥和一个圆柱组成的，
且圆锥在上，圆柱在下，
故符合题意的只有选项D.
故选D.
9.
【答案】
C
【考点】
斜二测画法画直观图
【解析】
根据斜二测画法的规则，分别判断每个图象的变化情况即可
【解答】
根据斜二测画法的规则可知，平行于坐标轴的直线平行性不变，
平行x轴的线段长度不变，平行于y轴的长度减半；
对于A，平面图形中的直角，在直观图中变为45∘或135∘角，不再相等，A错误；
对于B，根据斜二测画法知，相等的线段在直观图中不一定相等，B错误；
对于C，根据平行性不变原则，平行四边形的直观图仍然是平行四边形，C正确；
对于D，菱形的直观图中高的长度减半，对应的直观图不再是菱形，D错误．
10.
【答案】
A
【考点】
由三视图求体积（切割型）
【解析】
本题考查了三棱锥的三视图、体积计算公式，考查了推理能力与计算能力，属于中档题．由三视图可知：该几何体为三棱锥P−ABC，过点P作PD⊥底面ABC，垂足D在AC的延长线上，且BD⊥AD，AC=CD=1，BD=2，PD=2，即可得出．
【解答】
解：由三视图可知：该几何体为三棱锥P−ABC（如图），
过点P作PD⊥底面ABC，垂足D在AC的延长线上，
且BD⊥AD，AC=CD=1，BD=2，PD=2，
∴ 该几何题的体积V=13×12×1×2×2=23．
故选A．
11.
【答案】
C
【考点】
由三视图求外接球问题
球的表面积和体积
【解析】
首先把三视图转换为几何体，进一步求出外接球的半径，最后求出球的表面积．
【解答】
解：根据几何体的三视图转换为直观图为：该几何体为边长为1的正方体中切出一个三棱锥体A−BCD，
如图所示：
设外接球的半径为r，则：(2r)2=12+12+12=3，解得r2=34，
所以S=4⋅π⋅34=3π．
故选C．
12.
【答案】
C
【考点】
简单组合体的结构特征
【解析】
无
【解答】
解：根据长、宽分别是40米、30米得金字塔的底面对角线长50米，
上方四棱锥的高为45−32−6=7米，
所以四棱锥的侧棱长为72+252=674米，
则陵墓的高与金字塔的侧棱长之比大约为45674≈1.73．
故选C．
二、 填空题 （本题共计 4 小题 ，每题 5 分 ，共计20分 ）
13.
【答案】
234π2+9
【考点】
多面体和旋转体表面上的最短距离问题
【解析】
把AA′，BB′展开到一个平面，得到一个矩形，矩形长即弧AB的长，再利用勾股定理，即可得出结论．
【解答】
解：把AA′，BB′展开到一个平面，得到一个矩形，矩形长即弧AB的长，2π3×2=4π3，
∴ 一蚂蚁从A点沿圆柱表面爬到P点的最短路程为(4π3)2+22=16π29+4=234π2+9．
故答案为：234π2+9．
14.
【答案】
32
【考点】
多面体的内切球问题
【解析】
作出轴截面，利用Rt△AOE∽Rt△ACD，即可求出球的半径OE．
【解答】
解：如图所示，
作出轴截面，
∵ CD=3，AD=4，
∴ AC=5，∵ Rt△AOE∼Rt△ACD，
∴ OEAO=CDAC．
设OE=R，则AO=4−R，
∴ R4−R=35，
∴ R=32．
故答案为：32．
15.
【答案】
202
【考点】
平面图形的直观图
【解析】
根据平面图形与它的直观图的面积比为定值，列出方程即可求出结果．
【解答】
解：设梯形ABCD的面积为S，直观图A′B′C′D′的面积为S′=10，
则S′S=12sin45∘=24，
解得S=22S′=202．
答案：202．
16.
【答案】
3π
【考点】
柱体、锥体、台体的体积计算
圆锥的特征
【解析】
通过侧面展开图的面积和周长求出圆锥的母线和底面圆半径，即可求出圆锥的高，进而得解圆锥的体积．
【解答】
解：设圆锥的母线长为l，底面半径为r，
由题意得6π=12πl2，
所以l=23，
又它的侧面展开图是一个半圆，
所以2πr=πl，
所以r=3，
所以该圆锥的高为h=l2−r2=12−3=3，
所以此圆锥的体积为V=13πr2h=13π×32×3=3π.
故答案为：3π.
三、 解答题 （本题共计 6 小题 ，每题 11 分 ，共计66分 ）
17.
【答案】
解：设圆台的轴截面为等腰梯形ABCD如图所示：
则有AB=10cm，AM=8cm，则BM=6cm.
已知下底面面积为64πcm2，可得底面半径OB=8cm，
从而OM=O1A=2cm，
延长BA，OO1交于点S，设截得此圆台的圆锥的母线长为lcm，
则由△SAO1∼△SBO，
得SASB=AO1BO，即l−10l=28，
解得l=403cm.
【考点】
柱体、锥体、台体的侧面积和表面积
棱台的结构特征
【解析】
此题暂无解析
【解答】
解：设圆台的轴截面为等腰梯形ABCD如图所示：
则有AB=10cm，AM=8cm，则BM=6cm.
已知下底面面积为64πcm2，可得底面半径OB=8cm，
从而OM=O1A=2cm，
延长BA，OO1交于点S，设截得此圆台的圆锥的母线长为lcm，
则由△SAO1∼△SBO，
得SASB=AO1BO，即l−10l=28，
解得l=403cm.
18.
【答案】
解：(1)建立空间直角坐标系B1−xyz；
(2)在x轴上作线段B1C1=2cm，在y轴上作线段B1A1=1cm；
(3)过C1作y轴的平行线，过A1作x轴的平行线，使得两条平行线交于D1点；
(4)分别过A1，B1，C1，D1作z轴的平行线，使得A1A=B1B=C1C=D1D=3cm．
(5)连结AB，BC，CD，AD，则ABCD−A1B1C1D1就是要做的直观图．
【考点】
空间几何体的直观图
【解析】
根据斜二侧画法作图．
【解答】
解：(1)建立空间直角坐标系B1−xyz；
(2)在x轴上作线段B1C1=2cm，在y轴上作线段B1A1=1cm；
(3)过C1作y轴的平行线，过A1作x轴的平行线，使得两条平行线交于D1点；
(4)分别过A1，B1，C1，D1作z轴的平行线，使得A1A=B1B=C1C=D1D=3cm．
(5)连结AB，BC，CD，AD，则ABCD−A1B1C1D1就是要做的直观图．
19.
【答案】
解：(1)圆心在体对角线AC1的中点处，
2R2=32+42+52=50，
∴S=(2R)2π=50π．
(2)如图，设上底面中心为O1，下底面中心为O2，
刍童外接球的球心为O，则O，O1,O2共线，
连接O1E，O2A，OE，OA，
由已知可得O1E=EF2+EH22=5，
O2A=AB2+AD22=22 ，O1O2=1，
设该刍童的外接球的半径为R， OO2=h，
则R2=8+h2 ，R2=5+h+12，
联立解得R2=9 ，
∴该刍童的外接球的体积为V=43πR3=36π．
【考点】
球的表面积和体积
球内接多面体
【解析】
无
无
【解答】
解：(1)圆心在体对角线AC1的中点处，
2R2=32+42+52=50，
∴S=(2R)2π=50π．
(2)如图，设上底面中心为O1，下底面中心为O2，
刍童外接球的球心为O，则O，O1,O2共线，
连接O1E，O2A，OE，OA，
由已知可得O1E=EF2+EH22=5，
O2A=AB2+AD22=22 ，O1O2=1，
设该刍童的外接球的半径为R， OO2=h，
则R2=8+h2 ，R2=5+h+12，
联立解得R2=9 ，
∴该刍童的外接球的体积为V=43πR3=36π．
20.
【答案】
解：图中的几何体可看成是一个底面为直角梯形的直棱柱．
直角梯形的上底为1，下底为2，高为1，棱柱的高为1．
可求得直角梯形的四条边的长度为1，1，2， 2，
所以此几何体的体积V=S梯形h=121+2×1×1=32cm3；
表面积S=2S底面+S侧面=121+2×1×2+1+1+2+2×1
=(7+2)cm2，
所以表面积为：(7+2)cm2；体积为:32cm3.
【考点】
由三视图求体积
由三视图求表面积
【解析】
三视图复原几何体是底面为放倒的直角梯形的直棱柱，依据三视图的数据，求出表面积和体积．
【解答】
解：图中的几何体可看成是一个底面为直角梯形的直棱柱．
直角梯形的上底为1，下底为2，高为1，棱柱的高为1．
可求得直角梯形的四条边的长度为1，1，2， 2，
所以此几何体的体积V=S梯形h=121+2×1×1=32cm3；
表面积S=2S底面+S侧面=121+2×1×2+1+1+2+2×1
=(7+2)cm2，
所以表面积为：(7+2)cm2；体积为:32cm3.
21.
【答案】
解：(1)由三视图中可以看出，该几何体是组合体，上面的几何体是圆锥，下面的几何体是长方体，且圆锥底面圆和长方体上底的一组对边相切；
(2)易得圆锥的母线长为32+12=10，
∴ 表面积S=S圆锥侧+S长方体−S锥底
=π×1×10+2×(2×3+1×3+1×2)−π×12
=(10−1)π+22(m2)，
体积为V=13π×12×3+3×2×1=6+π(m3)．
故所求几何体的表面积是[(10−1)π+22]m2，体积是(6+π)m3.
【考点】
由三视图求表面积（组合型）
由三视图求体积（组合型）
简单组合体的结构特征
【解析】
（1）由三视图知几何体上面是圆锥，下面是长方体由三视图知几何体；
（2）由圆锥的母线长为3，底面圆的半径为1，得：圆锥母线长32+1=10，长方体的长、宽、高分别为3、2、1；根据表面积S=S圆锥侧+S长方体−S圆锥底求几何体的表面积，体积V=V长方体+V圆锥求几何体的体积．
【解答】
解：(1)由三视图中可以看出，该几何体是组合体，上面的几何体是圆锥，下面的几何体是长方体，且圆锥底面圆和长方体上底的一组对边相切；
(2)易得圆锥的母线长为32+12=10，
∴ 表面积S=S圆锥侧+S长方体−S锥底
=π×1×10+2×(2×3+1×3+1×2)−π×12
=(10−1)π+22(m2)，
体积为V=13π×12×3+3×2×1=6+π(m3)．
故所求几何体的表面积是[(10−1)π+22]m2，体积是(6+π)m3.
22.
【答案】
解：(1)由题设可知，几何体是一个高为2的四棱锥，其底面是长、宽分别为8和6的矩形，正侧面及其相对侧面均为底边长为8，高为h1的等腰三角形，左、右侧面均为座边长为6，高为h2的等腰三角形，如图所示．
∵h1=32+22=13，
h2=42+22=25，
∴几何体的侧面离积为S侧=2×12×6×25+12×8×13=125+813，
故S锥=5侧+S底=125+813+48．
(2)几何体的体积为V=13⋅S底⋅h=13×6×8×2=32．
【考点】
由三视图求体积
由三视图求表面积
【解析】
无
无
【解答】
解：(1)由题设可知，几何体是一个高为2的四棱锥，其底面是长、宽分别为8和6的矩形，正侧面及其相对侧面均为底边长为8，高为h1的等腰三角形，左、右侧面均为座边长为6，高为h2的等腰三角形，如图所示．
∵h1=32+22=13，
h2=42+22=25，
∴几何体的侧面离积为S侧=2×12×6×25+12×8×13=125+813，
故S锥=5侧+S底=125+813+48．
(2)几何体的体积为V=13⋅S底⋅h=13×6×8×2=32．