高中人教B版 (2019)11.4.2 平面与平面垂直教学演示ppt课件

这是一份高中人教B版 (2019)11.4.2 平面与平面垂直教学演示ppt课件，共22页。PPT课件主要包含了问题1二面角等内容，欢迎下载使用。
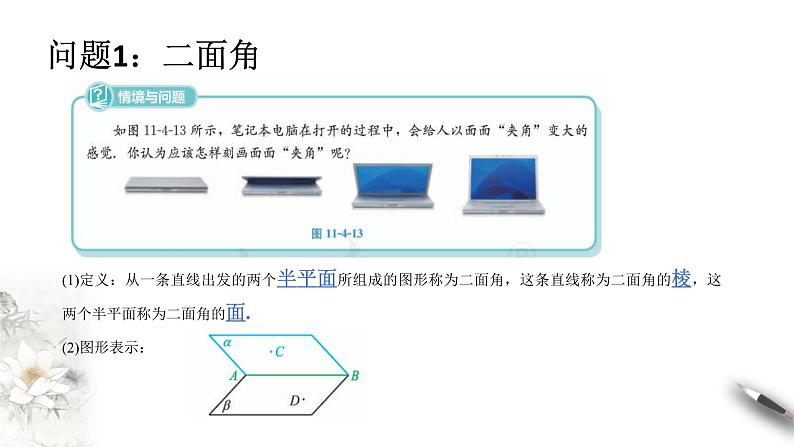
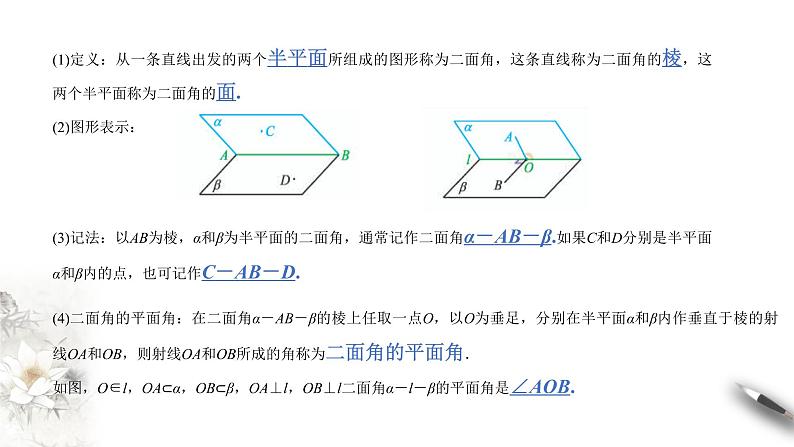
(1)定义：从一条直线出发的两个半平面所组成的图形称为二面角，这条直线称为二面角的棱，这两个半平面称为二面角的面.
(3)记法：以AB为棱，α和β为半平面的二面角，通常记作二面角α－AB－β.如果C和D分别是半平面α和β内的点，也可记作C－AB－D.
(4)二面角的平面角：在二面角α－AB－β的棱上任取一点O，以O为垂足，分别在半平面α和β内作垂直于棱的射线OA和OB，则射线OA和OB所成的角称为二面角的平面角．如图，O∈l，OA⊂α，OB⊂β，OA⊥l，OB⊥l二面角α－l－β的平面角是∠AOB.
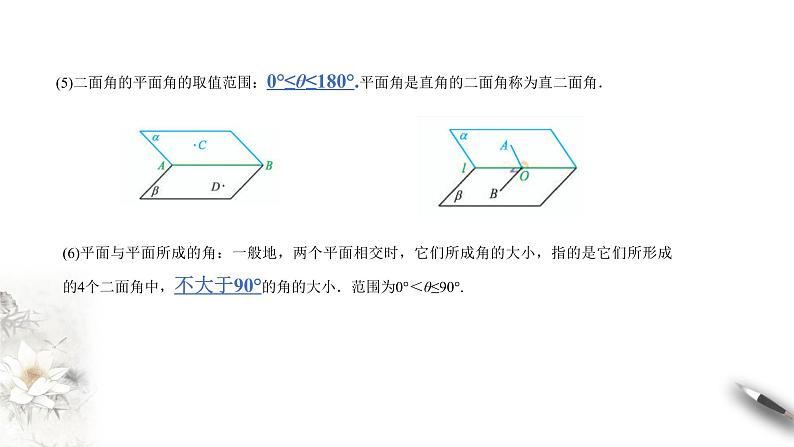
(5)二面角的平面角的取值范围：0°≤θ≤180°.平面角是直角的二面角称为直二面角．
(6)平面与平面所成的角：一般地，两个平面相交时，它们所成角的大小，指的是它们所形成的4个二面角中，不大于90°的角的大小．范围为0°＜θ≤90°.
【对点快练】判断正误.(1)两个相交平面组成的图形叫做二面角. ( )(2)异面直线a,b分别和一个二面角的两个半平面垂直,则a,b所成的角与这个二面角的平面角相等或互补. ( )(3)二面角的平面角是从棱上一点出发,分别在两个半平面内作射线所成角的最小角. ( )(4)二面角的大小与其平面角的顶点在棱上的位置没有关系. ( )
答案:(1)×　(2)√　(3)×　(4)√
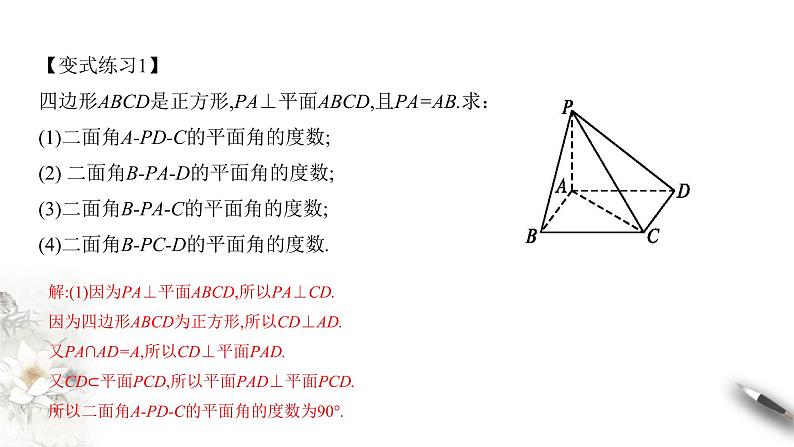
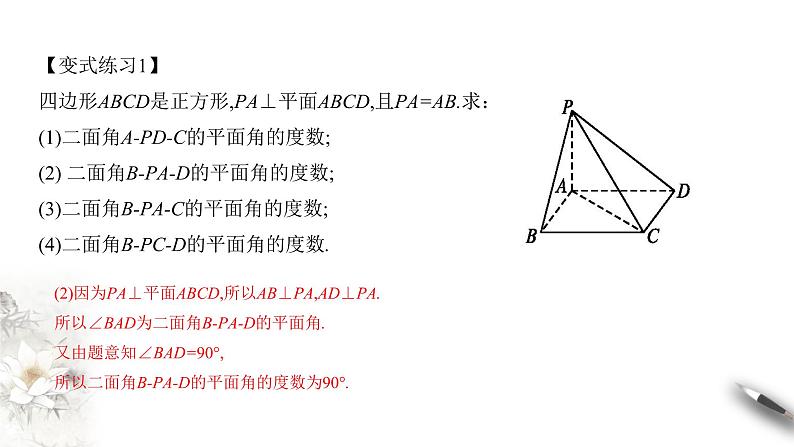
【变式练习1】四边形ABCD是正方形,PA⊥平面ABCD,且PA=AB.求：(1)二面角A-PD-C的平面角的度数;(2) 二面角B-PA-D的平面角的度数;(3)二面角B-PA-C的平面角的度数;(4)二面角B-PC-D的平面角的度数.
解:(1)因为PA⊥平面ABCD,所以PA⊥CD.因为四边形ABCD为正方形,所以CD⊥AD.又PA∩AD=A,所以CD⊥平面PAD.又CD⊂平面PCD,所以平面PAD⊥平面PCD.所以二面角A-PD-C的平面角的度数为90°.
(2)因为PA⊥平面ABCD,所以AB⊥PA,AD⊥PA.所以∠BAD为二面角B-PA-D的平面角.又由题意知∠BAD=90°,所以二面角B-PA-D的平面角的度数为90°.
(3)因为PA⊥平面ABCD,所以AB⊥PA,AC⊥PA.所以∠BAC为二面角B-PA-C的平面角.又四边形ABCD为正方形,所以∠BAC=45°.所以二面角B-PA-C的平面角的度数为45°.
【变式练习1】四边形ABCD是正方形,PA⊥平面ABCD,且PA=AB.求：(4)二面角B-PC-D的平面角的度数.
(4)作BE⊥PC于点E,连接DE,BD,且BD与AC交于点O,连接EO,如图.由题意知△PBC≌△PDC,则∠BPE=∠DPE,从而△PBE≌△PDE.所以∠DEP=∠BEP=90°,且BE=DE.所以∠BED为二面角B-PC-D的平面角.又PA⊥平面ABCD,所以PA⊥BC.又AB⊥BC,PA∩AB=A,所以BC⊥平面PAB.所以BC⊥PB.设AB=a,则PA=AB=BC=a,
【解题方法】方法一(定义法):在二面角的棱上找一个特殊点,在两个半平面内分别作垂直于棱的射线.如图所示,∠AOB为二面角α-a-β的平面角.
方法二(垂线法):过二面角的一个面内的一点作另一个平面的垂线,过垂足作棱的垂线,利用线面垂直可找到二面角的平面角或其补角.如图所示,∠AFE为二面角A-BC-D的平面角.
方法三(垂面法):过棱上一点作棱的垂直平面,该平面与二面角的两个半平面产生交线,这两条交线所成的角,即二面角的平面角.如图所示,∠AOB为二面角α-l-β的平面角.
【变式练习2】已知Rt△ABC,斜边BC⊂α,点A∉α,AO⊥α,O为垂足,∠ABO=30°,∠ACO=45°,求二面角A-BC-O的大小.
解:如图所示,在平面α内,过点O作OD⊥BC,垂足为点D,连接AD.设OC=a,∵AO⊥α,BC⊂α,∴AO⊥BC.又∵AO∩OD=O,∴BC⊥平面AOD.∵ AD⊂平面AOD,∴AD⊥BC,∴∠ADO是二面角A-BC-O的平面角.由AO⊥α,OB⊂α,OC⊂α知AO⊥OB,AO⊥OC.又∠ABO=30°,∠ACO=45°, 
问题2：平面与平面垂直
1．定义：一般地，如果两个平面α与β所成角的大小为90°，则称这两个平面互相垂直，记作α⊥β.
3．判定定理(1)文字叙述：如果一个平面经过另外一个平面的一条垂线，则这两个平面互相垂直．
(3)符号表示：如果l⊂α，l⊥β，则α⊥β.
(4)作用：证明平面与平面垂直.
注：由面面垂直的判定定理，容易证明直棱柱的每个侧面都与底面互相垂直，理由是直棱柱的侧棱垂直于底面。
【对点快练】1．经过平面α外一点和平面α内一点与平面α垂直的平面有________个．
答案：1个或无数个　设平面外一点为A，平面内一点为B，过点A作平面α的垂线l，若点B恰为垂足，则所有过AB的平面均与α垂直，此时有无数个平面与α垂直；若点B不是垂足，则l与点B确定唯一平面β满足α⊥β.
2．在三棱锥P－ABC中，已知PA⊥PB，PB⊥PC，PC⊥PA，如图，则在三棱锥P－ABC的四个面中，互相垂直的面有________对．
答案：3　平面PAB⊥平面PAC，平面PAB⊥平面PBC，平面PAC⊥平面PBC．
例2.如图，在正三棱柱ABC－A1B1C1中，D为BC的中点，点E在AC上，且DE⊥A1E.
(1)求证：平面A1AD⊥平面BCC1B1；(2)求证：平面A1DE⊥平面ACC1A1.
证明　(1)∵ABC－A1B1C1为正三棱柱，∴BB1⊥平面ABC，又AD⊂平面ABC，∴AD⊥BB1，又D为BC的中点，∴AD⊥BC，又BC∩BB1＝B，BC，BB1⊂平面BCC1B1.∴AD⊥平面BCC1B1.又AD⊂平面ADA1，∴平面A1AD⊥平面BCC1B1.
(2)∵ABC－A1B1C1为正三棱柱，∴AA1⊥平面ABC，又DE⊂平面ABC，∴AA1⊥DE，∵DE⊥A1E，又A1E∩AA1＝A1，∴DE⊥平面ACC1A1，又DE⊂平面A1DE，∴平面A1DE⊥平面ACC1A1.
【解题方法】面面垂直的方法(1)定义法:即说明两个半平面所成的二面角是直二面角;(2)判定定理法:在其中一个平面内寻找一条直线与另一个平面垂直,即把问题转化为“线面垂直”;(3)性质法:两个平行平面中的一个垂直于第三个平面,则另一个也垂直于此平面.
【变式练习1】　若本例改为：在正三棱柱ABC－A1B1C1中，F为A1C1的中点，求证：平面AB1F⊥平面ACC1A1.
【变式练习2】如图所示,已知∠BSC=90°,∠BSA=∠CSA=60°,又SA=SB=SC.求证:平面ABC⊥平面SBC.
证明:方法一:(利用定义证明)∵∠BSA=∠CSA=60°,SA=SB=SC,∴△ASB和△ASC是等边三角形,令SA=SB=SC=AB=AC=a,则△ABC和△SBC为共底边BC的等腰三角形.取BC的中点D,如图所示,连接AD,SD,
方法二:(利用判定定理)∵SA=SB=SC,且∠BSA=∠CSA=60°,∴SA=AB=AC,∴点A在平面SBC上的射影为△SBC的外心.∵△SBC为直角三角形,∴点A在△SBC上的射影D为斜边BC的中点,∴AD⊥平面SBC.又∵AD⊂平面ABC,∴平面ABC⊥平面SBC.