2021届黑龙江省大庆市高三第二次质量检测数学（文）试题

这是一份2021届黑龙江省大庆市高三第二次质量检测数学（文）试题，共17页。试卷主要包含了04，选修4-4，024等内容，欢迎下载使用。

2021.04
注意事项:
答卷前，考生务必将自己的姓名和准考证号填写在答题卡上．
回答选择题时，选出每道小题答案后，用铅笔把答题卡对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其他答案标号．回答非选择题时，将答案写在答题卡上．写在本试卷上无效．
第I卷（选择题 共60分）
一、选择题：本大题共12小题，每小题5分，满分60分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1．已知集合，，则
A．B．C．D．
2．设是虚数单位，则复数对应的点在复平面内位于
A．第一象限 B．第二象限 C．第三象限 D．第四象限
3．命题“”的否定是
A．B．
C．D．
4．
A．B．C．D．
5．已知直线与圆相交于两点，则弦的长度为
A．B． C． D．
6．已知是三条不同的直线，是两个不同的平面，则下列判断不正确的是
A．若，，则．
B．若都与相交且，则直线共面．
C．若，，，则．
D．若两两相交，且交于同一点，则直线共面．
7．已知向量，则x的值为
A． B． C． D．
8．日晷是我国古代按照日影测定时刻的仪器，晷长即为所测量影子的长度．我国天文学和数学著作《周髀算经》中记载：一年有二十四个节气，每个节气的晷长损益相同． 二十四节气及晷长变化如图所示，相邻两个节气晷长减少或增加的量相同，如此周而复始． 已知每年冬至的晷长为一丈三尺五寸，夏至的晷长为一尺五寸(一丈等于十尺，一尺等于十寸)，则下列说法不正确的是

A．白露比立秋的晷长长两尺 B．大寒的晷长为一丈五寸
C．处暑和谷雨两个节气的晷长相同 D．立春的晷长比立秋的晷长长
9．定义在上的函数满足，，当时，
，则函数的图象与的图象的交点个数为
A． B． C． D．
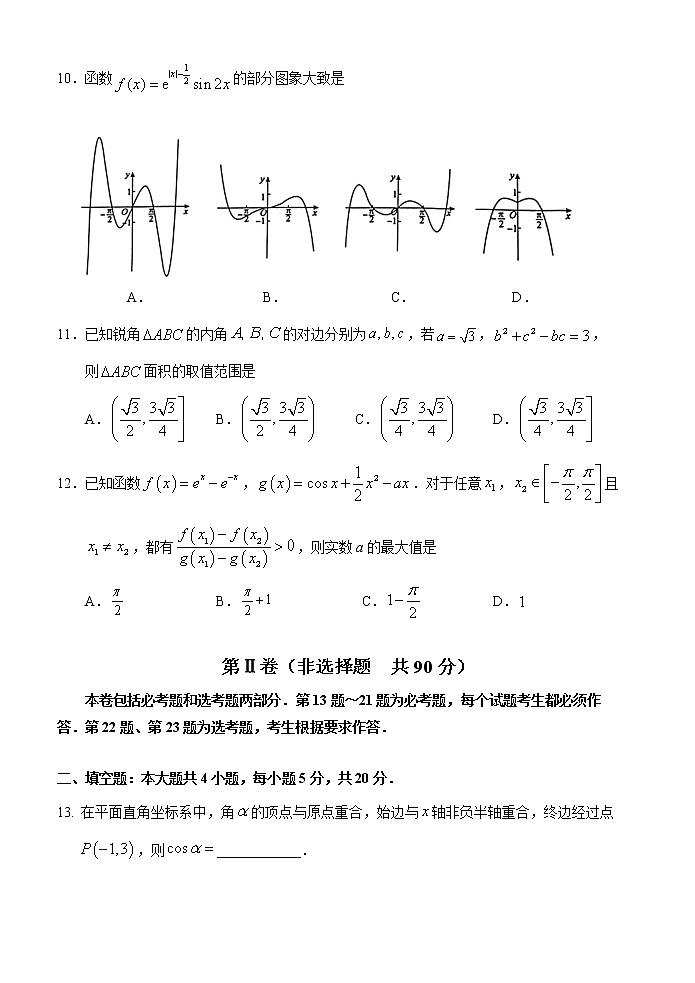
10．函数的部分图象大致是


A． B． C． D．
11．已知锐角的内角的对边分别为，若，，
则面积的取值范围是
A． B． C． D．
12．已知函数，．对于任意，且
，都有，则实数a的最大值是
A． B． C． D．
第Ⅱ卷（非选择题 共90分）
本卷包括必考题和选考题两部分．第13题～21题为必考题，每个试题考生都必须作答．第22题、第23题为选考题，考生根据要求作答．
二、填空题：本大题共4小题，每小题5分，共20分．
13. 在平面直角坐标系中，角的顶点与原点重合，始边与轴非负半轴重合，终边经过点
，则____________．
14．若满足约束条件，则的最小值为____________．
15．某机构一年需购买消毒液吨，每次购买吨，每次运费为3万元，一年的总存储费用为万元．要使一年的总运费与总存储费用之和最小，则的值是____________．
16．已知抛物线，圆与轴相切，斜率为的直线过抛物线的焦点与抛物线交于两点，与圆交于两点（两点在轴的同一侧），若，则的值为____________．
三、解答题：共70分．解答应写出必要的文字说明、证明过程和演算步骤．
17.（本小题满分12分）
已知数列的前项和为，且．
（1）求数列的通项公式；
（2）若，求数列的前项和．
18.（本小题满分12分）
随着新冠疫情防控进入常态化，人们的生产生活逐步步入正轨．为拉动消费，某市政府分批
发行亿元政府消费券．为了解政府消费券使用人群的年龄结构情况，在发行完第一批政府
消费券后，该市政府采用随机抽样的方法在全市市民中随机抽取了人，对是否使用过政
府消费券的情况进行调查，部分结果如下表所示，其中年龄在岁及以下的人数占样本总
数的，没使用过政府消费券的人数占样本总数的．
（1）请将题中表格补充完整，并判断是否有的把握认为该市市民是否使用政府消费券
与年龄有关？
（2）现从岁及以下的样本中按是否使用过政府消费券进行分层抽样，抽取人做进一步
访谈，然后再从这人中随机抽取人填写调查问卷，则抽取的人中恰好一个使用过
政府消费券，一个没使用过政府消费券的概率为多少？
附：，其中．
19.（本小题满分12分）
如图所示，正方体中，棱长为2，且分
别为的中点．
（1）求证：∥平面；
（2）求四面体的体积．
20.（本小题满分12分）
已知椭圆的长轴长为，离心率为．
（1）求椭圆的方程；
（2）设为椭圆右顶点，过点作斜率不为的直线与曲线交于两点，
求证：．

21.（本小题满分12分）
已知函数．
（1）讨论的单调性；
（2）若有两个相异零点，求证:．
请考生在第22、23二题中任意选一题作答，如果多做，则按所做的第一题记分．作答时，用铅笔在答题卡上把所选题目对应的题号涂黑．
22.（本小题满分10分）选修4-4：坐标系与参数方程
在直角坐标系中，直线的参数方程为（为参数），以坐标原点为极点，
轴正半轴为极轴建立极坐标系，曲线的极坐标方程为．
（1）求直线的普通方程和曲线的直角坐标方程；
（2）已知点，若直线与曲线相交于不同的两点，求的值．
23.（本小题满分10分）选修4-5：不等式选讲
设函数的最小值为．
（1）求；
（2）设均为正实数，且，证明：．
文科数学答案及评分标准
选择题：本大题共12小题，每小题5分，满分60分.
二、填空题:本大题共4小题，每小题5分，共20分.
13. ； 14. ； 15. ； 16. .
三.解答题
17.（本小题满分12分）
解：（1）当时，
，
解得， ……………1分
当时，
， ……………3分
得，
因为，
所以，
因为，
所以数列是以3为首项，3为公比的等比数列， ……………5分
所以. ……………6分
（2）因为， ……………7分
所以， ……………9分
所以数列的前项和
. ……………12分
18.（本小题满分12分）
解：（1）由题意得，总人数为200人，年龄在45岁及以下的人数为人，
没使用过政府消费券的人数为人，
完成表格如下：
……………2分
由列联表可知， ……………4分
因为，
所以有90%的把握认为该市市民民是否使用政府消费券与年龄有关． ……………6分
由题意可知，
从45岁及以下的市民中采用分层抽样的方法可以抽取使用过政府消费券的市民6人，
没有使用过政府消费券的市民2人， ……………7分
设使用过政府消费券的人为1，2，3，4，5，6，没使用过政府消费券的人为，，则全部情况为：
12，13，14，15，16，23，24，25，26，34，35，36，45，46，56，1，2，3，4，5，6，1，2，3，4，5，6，， 共计28种情况， ……………9分
其中，一个使用过政府消费券，一个没使用过政府消费券的情况有12种， ……………10分
所以恰好抽到“一个使用过政府消费券，一个没使用过政府消费券”的概率为．………12分
19.（本小题满分12分）
取中点为，连接、，
因为是正方体，点和为所在棱中点，
所以∥，，
所以四边形为平行四边形，
所以∥， ……………2分
在正方形中，点和为中点，
所以∥， ……………3分
所以∥， ……………4分
又因为，， ……………5分
所以//平面． ……………6分
（2）因为∥平面，
所以， ……………8分
在四面体中，
， ……………10分
到平面的距离为2，
所以． ……………12分
20．（本小题满分12分）
解：（1）因为椭圆的长轴长为4，
所以，即． ……………1分
又因为椭圆上的离心率为，
，
即， ……………2分
所以，
所以椭圆的方程为． ……………4分
（2）由（1）得，
因为，
设直线的方程为，， ……………5分
联立方程得，
化简得，
， ……………7分
且， ……………9分
因为，，
所以
， ……………11分
所以． ……………12分
21.（本小题满分12分）
解：由题意得， ……………1分
①时，恒成立，
所以，所以在单调递增． ……………3分
②时，在上，在上，
所以在单调递减，在单调递增． ……………5分
综上,
时，在单调递增．
时，在单调递减，在单调递增． ……………6分
（2）因为有两个相异零点，，
由（1）可知，，
不妨设，
因为，，
所以，，
所以， ……………7分
要证，
即证，
等价于证明，而，
所以等价于证明，
也就是. （*） ……………9分
令，则，
于是欲证（*）成立，等价于证明成立，
设函数，
求导得，
所以函数是上的增函数， ……………11分
所以，
即成立，
所以成立． ……………12分
22．（本小题满分10分）
解：（1）由（为参数），消去参数可得直线的普通方程为，
……………2分
由，
得，
即，
整理可得曲线的直角坐标方程为． ……………4分
（2）直线经过点，
将直线的参数方程（为参数）代入椭圆中，
整理得， ……………6分
显然，
设点，对应的参数分别为，，
则有，， ……………8分
因为同号，
故． ……………10分
23．（本小题满分10分）
解：（1）法一：
由绝对值三角不等式可得， ……………2分
当且仅当时，等号成立，
所以． ……………4分
法二：
因为．
= 1 \* GB3 ①当时，； ……………1分
= 2 \* GB3 ②当时，； ……………2分
= 3 \* GB3 ③当时，； ……………3分
综上，的最小值． ……………4分
（2）因为，
所以，
同理可得，， ……………6分
由基本不等式可得
， ……………9分
当且仅当时，等号成立，
因此． ……………10分
使用过政府消费券
没使用过政府消费券
总计
45岁及以下
90
45岁以上
总计
200
0.15
0.10
0.05
0.025
2.072
2.706
3.841
5.024
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
A
D
B
C
D
B
B
A
A
A
C
使用过政府消费券
没使用过政府消费券
总计
45岁及以下
90
30
120
45岁以上
50
30
80
总计
140
60
200