2020-2021学年第23章 图形的相似23.3 相似三角形3. 相似三角形的性质教课ppt课件

这是一份2020-2021学年第23章 图形的相似23.3 相似三角形3. 相似三角形的性质教课ppt课件，共20页。PPT课件主要包含了回顾复习，情境引入，对应边成比例，对应角相等，探索新知，相似三角形的性质，类似结论，自主思考---，由此可得以下结论，相似比等内容，欢迎下载使用。

(1)什么是相似三角形？相似比是什么？
对应角相等、对应边成比例的三角形,叫做相似三角形.
（2）如何判定两个三角形相似？
①平行得相似；②两个角对应相等；③两边对应成比例, 夹角相等；④三边对应成比例.
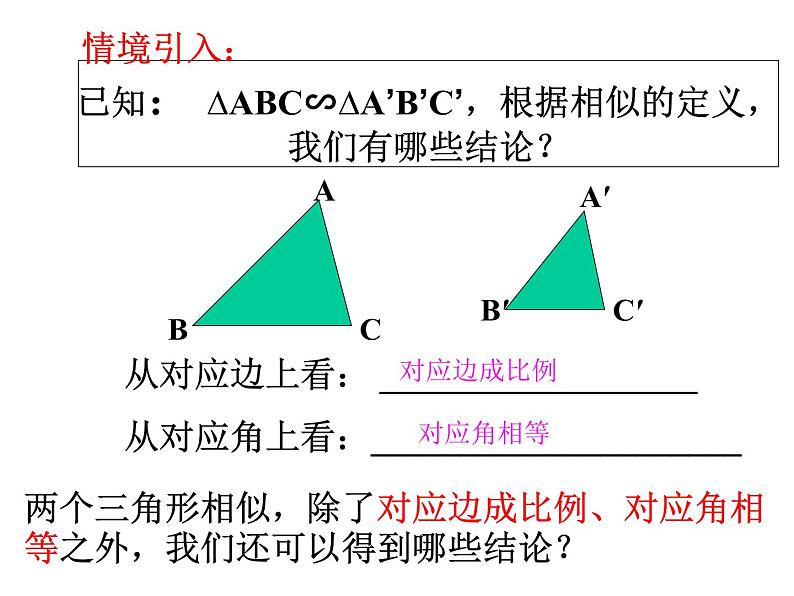
已知： ∆ABC∽∆A’B’C’，根据相似的定义，我们有哪些结论？
从对应边上看： __________________
从对应角上看：_____________________
两个三角形相似，除了对应边成比例、对应角相等之外，我们还可以得到哪些结论？
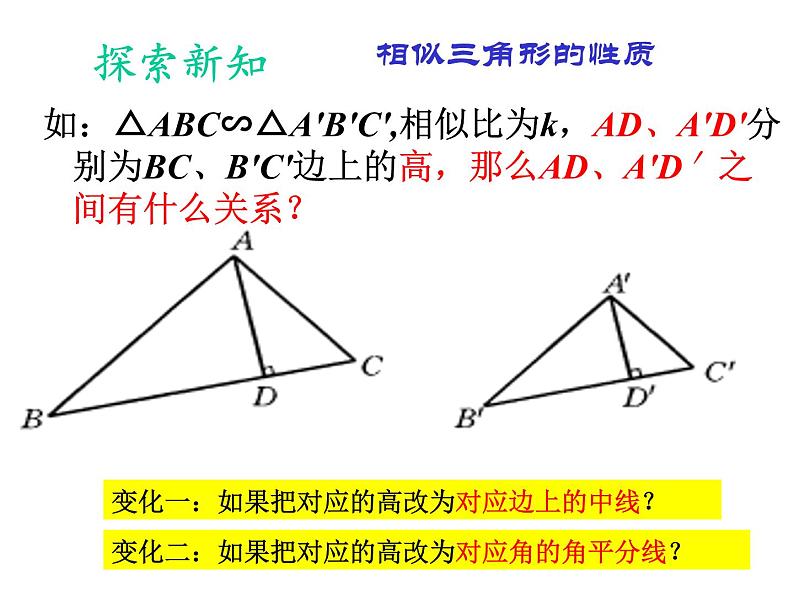
如：△ABC∽△A′B′C′,相似比为k，AD、A′D′分别为BC、B′C′边上的高，那么AD、A′D′之间有什么关系？
变化一：如果把对应的高改为对应边上的中线？
变化二：如果把对应的高改为对应角的角平分线？
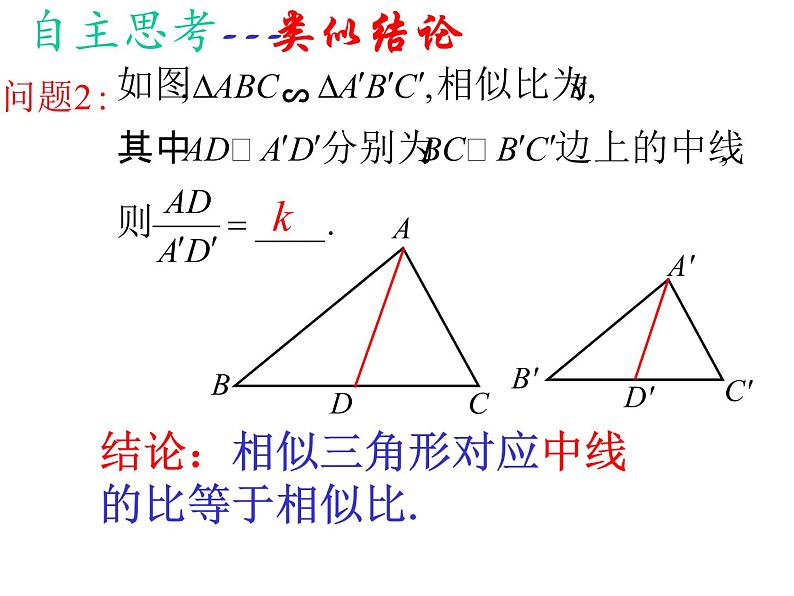
结论：相似三角形对应中线的比等于相似比.
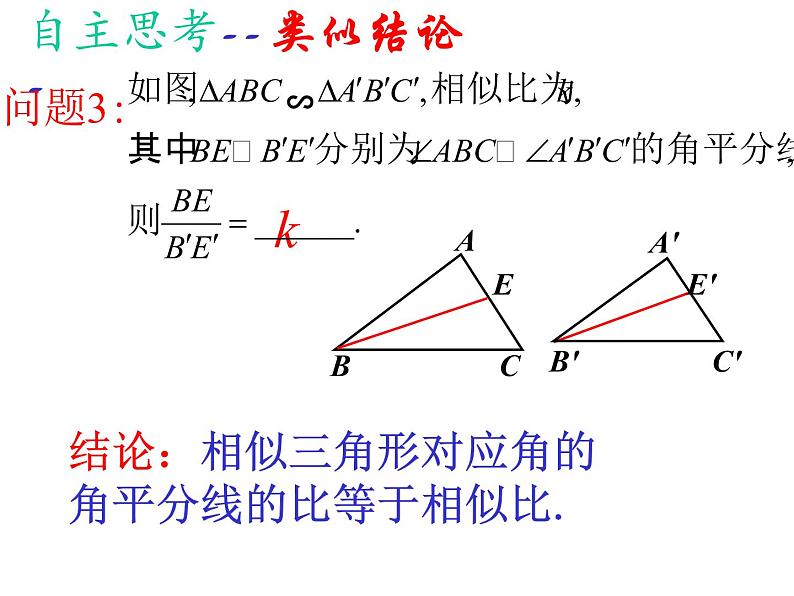
结论：相似三角形对应角的角平分线的比等于相似比.
相似三角形对应边上的高的比等于 相似三角形对应边上的中线的比等于相似三角形对应角的平分线的比等于
1.相似三角形对应边的比为2∶3,那么相似比为_________,对应角平分线的比为______.
2．两个相似三角形的相似比为1:4, 则对应高的比为_________,对应角的角平分线的比为_________.
图中(1)(2)(3)分别是边长为1、2、3的等边三角形，它们都相似吗？为什么？
（2）与（1）的相似比＝________________，  （2）与（1）的周长比＝________________;  （2）与（1）的面积比＝________________;（3）与（1）的相似比＝________________，  （3）与（1）的周长比＝________________.  （3）与（1）的面积比＝________________.  
猜想结论： 相似三角形的周长比等于_____________．  
相似三角形的面积比 等于___ ________． 
问题4：两个相似三角形的周长比
已知△ABC∽△ ，且相似比为k。求证：△ABC、 周长的比等于k
即△ABC、△ 的周长比等于相似比
结论：相似三角形对应角的周长的比等于相似比.
问题5:两个相似三角形的面积与
相似比之间有什么关系呢？
例:已知△ABC∽△ ,且相似比为k，AD、 分别是△ABC、△ 对应边BC、 、上的高，求证：
结论：相似三角形面积的比等于相似比的平方.
(1)△ADE与△ABC相似吗？如果相似， 求它们的相似比.
(2) △ADE的周长︰△ABC的周长＝_______.
例：如图，DE∥BC， DE = 1, BC = 4，
1：已知△ABC∽△DEF，BG、EH分别是△ABC和 △DEF的角平分线，BC＝6cm,EF＝4cm,BG＝4.8cm.求EH的长。
解：∵ △ABC∽△DEF 　
∴　BC∶EF＝BG∶EH
答：EH的长为3.2cm。
1、已知两个等边三角形的边长之比为 2 ：3，且它们的面积之和为26cm2，则较小的等边三角形的面积为多少？
我有哪些收获呢？与大家共分享！
学 而 不 思 则 罔
1、相似三角形对应边成____,对应角______. 2、相似三角形对应边上的高、对应边上的中线、 对应角平分线的比都等于________. 3、相似三角形周长的比等于________， 相似三角形面积的比等于______________.
相似多边形也有同样的结论哟！