数学九年级上册28.3 圆心角和圆周角授课课件ppt

这是一份数学九年级上册28.3 圆心角和圆周角授课课件ppt，共44页。PPT课件主要包含了学习目标，回顾与思考，轴对称性，圆具有旋转不变性，圆是中心对称图形，它的对称中心是圆心，弧AB弧A′B′，典例精析，证明∵，弧AB弧AC等内容，欢迎下载使用。

1.复习并巩固圆中的基本概念.2.理解并掌握圆心角的定义，能够运用其进行计算. (重点)3.理解并掌握圆心角、弧、弦间的关系.（难点）
问题1 圆的对称性有哪几方面？
问题2 将圆绕圆心任意旋转,你发现了什么？
圆是中心对称图形吗?它的对称中心在哪里?
圆心角：我们把顶点在圆心的角叫做圆心角.
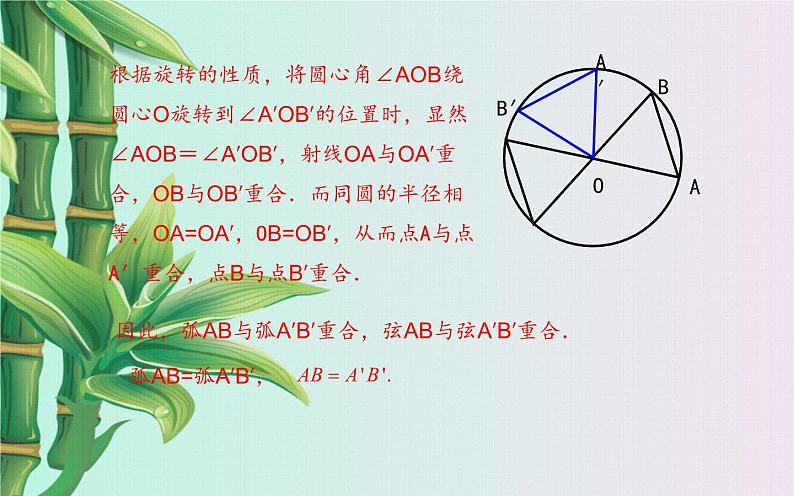
如图，将圆心角∠AOB绕圆心O旋转到∠A′ O B′ 的位置，你能发现哪些等量关系？为什么？
根据旋转的性质，将圆心角∠AOB绕圆心O旋转到∠A′OB′的位置时，显然∠AOB＝∠A′OB′，射线OA与OA′重合，OB与OB′重合．而同圆的半径相等，OA=OA′，OB=OB′，从而点A与点A′重合，点B与点B′重合．
因此，弧AB与弧A′B′重合，弦AB与弦A′B′重合．
同样，还可以得到：在同圆或等圆中，如果两条弧相等，那么它们所对的圆心角_____， 所对的弦________；在同圆或等圆中，如果两条弦相等，那么他们所对的圆心角______，所对的弧_________．
这样，我们就得到下面的定理：
在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等．
如图在⊙O中，弧AB=弧AC ，∠ACB=60°，求证：∠AOB=∠BOC=∠AOC.
∴ AB=AC, △ABC等腰三角形．
又 ∵∠ACB=60°，
∴ △ABC是等边三角形，AB=BC=CA.
∴ ∠AOB＝∠BOC＝∠AOC.
1. 如图，AB、CD是⊙O的两条弦．（1）如果AB=CD，那么___________， ________________．（2）如果弧AB=弧CD，那么____________，______________．（3）如果∠AOB=∠COD，那么_____________，____________．
相等
因为AB=CD ，所以∠AOB=∠COD.
又因为AO=CO，BO=DO，
所以△AOB≌ △COD.
又因为OE、OF分别是AB与CD边上的高，
（4）如果AB=CD，OE⊥AB于E，OF⊥CD于F，OE与OF相等吗？为什么？
2. 如图，AB是⊙O的直径，弧BC=弧CD=弧DE,∠COD=35°，求∠AOE的度数．
解：∵弧BC=弧CD=弧DE，
∴ ∠ BOC=∠COD=∠DOE=35°.
∵弧BC=弧CD=弧DE，
2.圆心角、弧、弦间的关系:1)在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等．
2)同圆或等圆中，两个圆心角、两条弧、两条弦中有一组量相等，它们所对应的其余各组量也相等．
1.圆心角：我们把顶点在圆心的角叫做圆心角.
圆心角和圆周角
1.复习圆心角的概念.2.理解并会判断圆周角.(重点)3.理解并掌握圆周角的性质并进行计算.（难点）
3.下列命题是真命题的是( )①在同圆中，相等的弦所对的圆心角相等；②相等的圆心角所对的弧相等;③圆既是轴对称图形,又是中心对称图形.A.①② B.①③ C.②③ D.①②③
答:顶点在圆心的角叫圆心角.
2.圆心角的度数和它所对的弧的度数的关系?
圆心角顶点发生变化时,我们得到几种情况?
思考：三个图中的∠BAC的顶点A各在圆的什么位置？ 角的两边和圆是什么关系？
你能仿照圆心角的定义给圆周角下定义吗?
圆周角定义: 顶点在圆上,两边都与圆相交的角叫圆周角.
②角的两边都与圆相交.
解:∵∠AOC是△ABO的外角，
∴∠AOC=∠B+∠A.
一条弧所对的圆周角等于它所对的圆心角的一半.
1.首先考虑一种特殊情况：当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系.
提示:能否转化为1的情况?
圆上一条弧所对的圆周角等于它所对的圆心角的一半.
如果圆心不在圆周角的一边上,结果会怎样?2.当圆心(O)在圆周角(∠ABC)的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?
提示:能否也转化为1的情况?
过点B作直径BD.由1可得:
3.当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?
圆周角定理:圆周角的度数等于它所对弧所得的圆心角度数的一半.
提示:圆周角定理是承上启下的知识点,要予以重视.
∵ ∠CAD=∠EBF ∴ 弧CD=弧EF
推论1：在同圆或等圆中，同弧或等弧所对的圆周角相等，相等的圆周角所对的弧也相等.
推论2：半圆或直径所对的圆周角是直角；90°的圆周角所对的弦是直径.
∵ AB是直径∴∠AC1B=90°
∵ ∠AC1B=90°∴ AB是直径.
∴ ∠AOB=2∠BOC
例.如图：OA，OB，OC都是⊙O的半径，∠AOB=2∠BOC. 求证：∠ACB=2∠BAC.
1.判断下列各图形中的角是不是圆周角.
2.如图，点B，C在⊙O上，且BO=BC，则圆周角∠BAC等于（ ）
4.如图，已知BD是⊙O的直径，⊙O的弦AC⊥BD于点E，若∠AOD=60°，则∠DBC的度数为（ ） A.30° B.40° C.50° D.60°
【规律方法】解决圆周角和圆心角的计算和证明问题,要准确找出同弧所对的圆周角和圆心角,然后再灵活运用圆周角定理.
定理：圆上一条弧都所对的圆周角等于它所对的圆心角的一半．
1.复习并巩固圆周角和圆心角的相关知识.2.理解并掌握圆内接四边形的概念及性质并学会运用. (重点)
问题1 什么是圆周角？
② 角的两边都与圆相交.
圆周角概念: 顶点在圆上,并且两边都和圆相交的角叫圆周角.
问题2 什么是圆周角定理？
圆周角定理:圆上一条弧所对的圆周角等于它所对的圆心角的一半.
若一个多边形各顶点都在同一个圆上，那么，这个多边形叫做圆内接多边形，这个圆叫做这个多边形的外接圆.
如图，四边形ABCD为⊙O的内接四边形；⊙O为四边形ABCD的外接圆.
∵ 弧BCD和弧BAD所对的圆心角的和是周角，
∴∠A＋∠C＝180°，
同理∠B＋∠D＝180°，
∠BCD＋∠DCE＝180°.
定理：圆的内接四边形的对角互补，且任何一个外角都等于它的内对角.
由于∠A是∠DCE的补角∠BCD的对角（简称∠DCE的内对角），于是我们得到圆内接四边形的性质：
1.在⊙O中，∠CBD=30°，∠BDC=20°,求∠A.
解：∵∠CBD=30°，∠BDC=20°∴∠C=180°-∠CBD-∠BDC=130°∴∠A=180°-∠C=50°（圆内接四边形对角互补）
变式：已知∠OAB等于40°,求∠C的度数.
2.判断.（1）等弧所对的圆周角相等；（ ）（2）相等的弦所对的圆周角也相等；（ ）（3）90°的角所对的弦是直径；（ ）（4）同弦所对的圆周角相等.（ ）
2.圆内接四边形的性质定理：圆的内接四边形的对角互补，且任何一个外角都等于它的内对角.
1.若一个四边形各顶点都在同一个圆上，那么，这个四边形叫做圆内接四边形，这个圆叫做这个四边形的外接圆.