初中人教版13.2.2 用坐标表示轴对称评课课件ppt

这是一份初中人教版13.2.2 用坐标表示轴对称评课课件ppt，共13页。PPT课件主要包含了教学目标，重点难点，教学设计等内容，欢迎下载使用。

1．能在直角坐标系中画点关于坐标轴的对称点．2．能表示点关于坐标轴对称的点的坐标，表示关于平行于坐标轴的直线的对称点的坐标．
重点用坐标表示点关于坐标轴对称的点的坐标．难点找对称点的坐标之间的关系．
一、问题导入教材图13.2－3是一张老北京城的示意图，其中西直门和东直门是关于中轴线对称的，如果以天安门为原点，分别以长安街和中轴线为x轴和y轴建立平面直角坐标系，根据如图所示的东直门的坐标，你能说出西直门的坐标吗？二、探究新知【探究1】　(1)在直角坐标系中画出下列已知点A(2，－3)，B(－1，2)，C(－6，－5)，D(3，5)，E(4，0)，F(0，－3)；(2)画出这些点分别关于x轴、y轴对称的点，并填写表格；
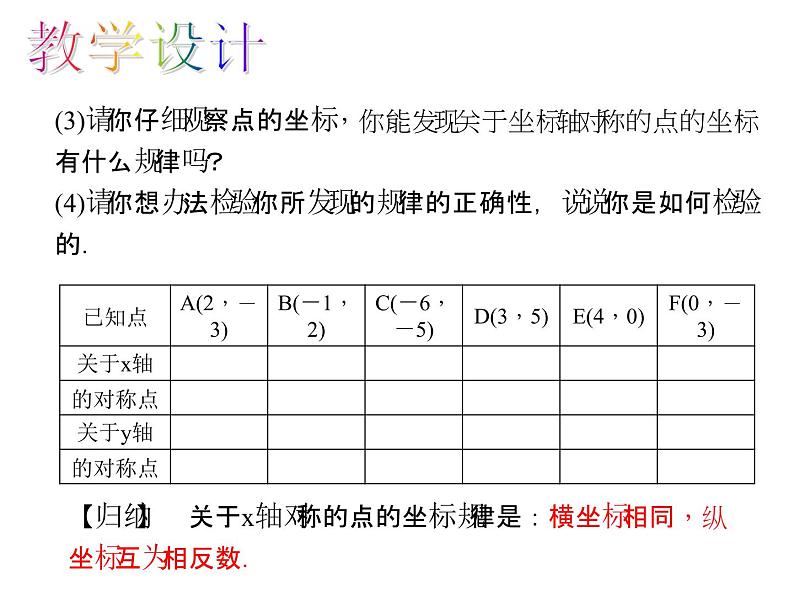
(3)请你仔细观察点的坐标，你能发现关于坐标轴对称的点的坐标有什么规律吗？(4)请你想办法检验你所发现的规律的正确性，说说你是如何检验的．
【归纳】　关于x轴对称的点的坐标规律是：横坐标相同，纵坐标互为相反数．
【探究2】　在同一平面直角坐标系内描出以上各点关于y轴的对称点并写出坐标，观察关于y轴对称的两个点的坐标有什么规律？【归纳】　关于y轴对称的点的坐标规律是：纵坐标相同，横坐标互为相反数．【探究3】　按以上规律，说出点P(x，y)关于x轴的对称点P1的坐标，再说出P1关于y轴的对称点P2坐标．观察点P经过两次轴对称所得点P2的坐标有什么规律？【归纳】　一个点经历关于x轴、y轴两次轴对称得到的对称点坐标规律是：横坐标互为相反数，纵坐标也互为相反数．在以后学了“中心对称”后，两点被称为关于原点对称．
三、举例分析【例1】　已知A(2，a)，B(－b，4)，分别根据下列条件求a，b的值．(1)A，B关于y轴对称；(2)A，B关于x轴对称；(3)A，C关于x轴对称，B，C关于y轴对称．【解析】　(1)A，B关于y轴对称，说明纵坐标相同，横坐标相反，a＝4，b＝2；(2)A，B关于x轴对称，说明横坐标相同，纵坐标相反，a＝－4，b＝－2；(3)A，C关于x轴对称，B，C关于y轴对称，说明A，B经过x轴、y轴两次对称变换，即关于原点对称，横、纵坐标各互为相反数，a＝－4，b＝2.
【例2】　如下图，四边形ABCD的四个顶点的坐标分别为A(－5，1)，B(－2，1)，C(－2，5)，D(－5，4)，分别画出与四边形ABCD关于y轴和x轴对称的图形．
学生独立完成，教师用多媒体出示出正确答案并讲评．
四、课堂巩固1．平面直角坐标系中，点P(4，－5)关于x轴的对称点在(　　)A．第一象限　　　　　　B．第二象限C．第三象限　　　　　　D．第四象限2．已知点P(－2，3)关于y轴对称点为Q(a，b)，则a＋b的值为(　　)A．1　　　　B．－1　　　　C．5　　　　D．－5
3．点P(a，b)关于x轴对称的点为P1，点P1关于y轴的对称点为P2，则P2的坐标为(　　)A．(a，b) B．(a，－b)C．(－a，b) D．(－a，－b)4．若点(a，b)与点(m，n)满足a＋m＝0，b－n＝0，则这两点关于(　　)对称．A．x轴 B．y轴C．x轴或y轴 D．不确定
五、拓展思维如图，点A(1，4)，B(4，1)，l为第一、三象限角∠xOy的平分线．(1)求证：l垂直平分AB；(2)A，B关于l成轴对称吗？(3)如果点A，B的坐标分别为(6，8)和(8，6)，它们还关于l对称吗？(4)如果你发现了对称点的坐标规律，写出点P(m，n)关于第一、三象限角平分线的对称点Q的坐标．
六、小结与作业小结：(1)点关于某条直线对称的点的坐标可以通过寻找线段之间的关系来求．(2)点(x，y)关于x轴对称的点的坐标为(x，－y)，即横坐标相等，纵坐标互为相反数；点(x，y)关于y轴对称的点的坐标为(－x，y)即横坐标互为相反数，纵坐标相等．作业：教材习题13.2第3，4题．