2018-2019学年北京市东城区汇文中学九上期中数学试卷

这是一份2018-2019学年北京市东城区汇文中学九上期中数学试卷，共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共8小题；共40分）
1. 如图，图中的图象对应的函数解析式可能是
A. y=5xB. y=2xC. y=−2xD. y=−1x

2. 如图，AB 为 ⊙O 的直径，C，D 为 ⊙O 上的两点，若 AB=14，BC=7．则 ∠BDC 的度数是
A. 15∘B. 30∘C. 45∘D. 60∘

3. 一个扇形的圆心角是 120∘，面积为 3π cm2，那么这个扇形的半径是
A. 1 cmB. 3 cmC. 6 cmD. 9 cm

4. 如图，在平面直角坐标系 xOy 中，点 A，B 分别为 △OCD 中边 OC，OD 上的两个点，且 AB∥CD，若点 A1,2，B2,0，C5,0，则点 A 的对应点 C 的坐标是
A. 2,5B. 52,5C. 3,5D. 3,6

5. 若抛物线 y=x2−2x+m 与 x 轴有交点，则 m 的取值范围是
A. m>1B. m≥1C. m<1D. m≤1

6. 如图，反比例函数 y=kx 在第二象限的图象上有一点 A，过点 A 作 AB⊥x 轴于 B，且 S△AOB=2，则 k 的值为
A. −4B. 2C. −2D. 4

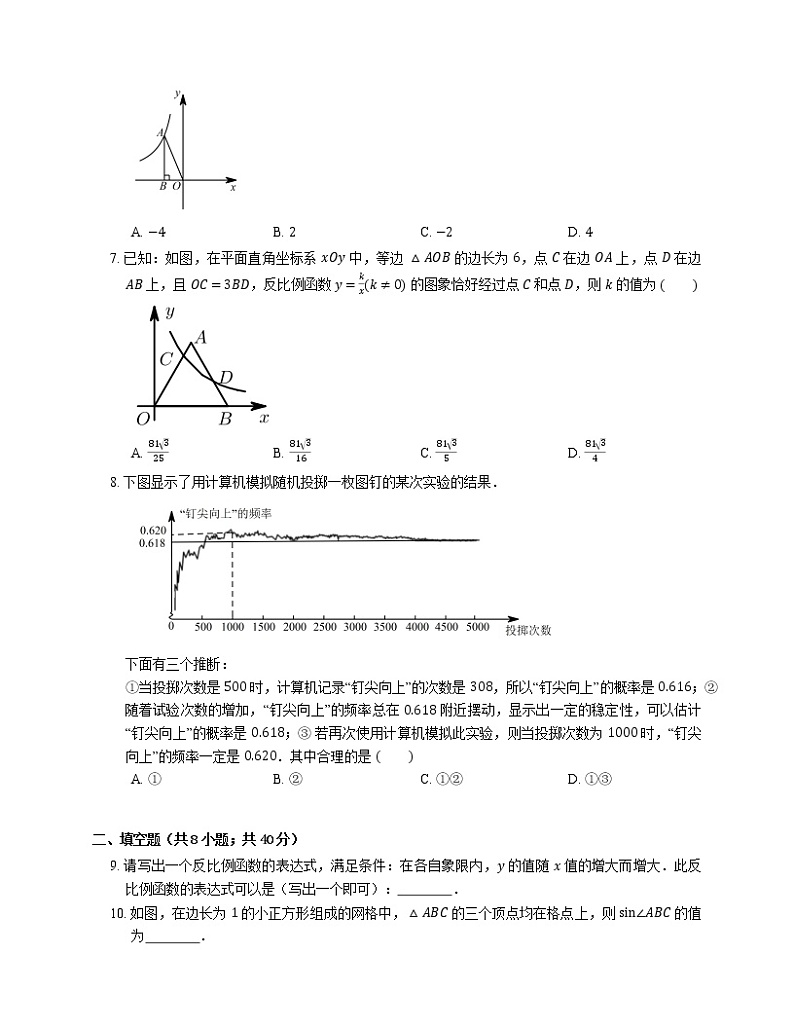
7. 已知：如图，在平面直角坐标系 xOy 中，等边 △AOB 的边长为 6，点 C 在边 OA 上，点 D 在边 AB 上，且 OC=3BD，反比例函数 y=kxk≠0 的图象恰好经过点 C 和点 D，则 k 的值为
A. 81325B. 81316C. 8135D. 8134

8. 下图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果．
下面有三个推断：
①当投掷次数是 500 时，计算机记录“钉尖向上”的次数是 308，所以“钉尖向上”的概率是 0.616；②随着试验次数的增加，“钉尖向上”的频率总在 0.618 附近摆动，显示出一定的稳定性，可以估计“钉尖向上”的概率是 0.618；③ 若再次使用计算机模拟此实验，则当投掷次数为 1000 时，“钉尖向上”的频率一定是 0.620．其中合理的是
A. ①B. ②C. ①②D. ①③

二、填空题（共8小题；共40分）
9. 请写出一个反比例函数的表达式，满足条件：在各自象限内，y 的值随 x 值的增大而增大．此反比例函数的表达式可以是（写出一个即可）： ．

10. 如图，在边长为 1 的小正方形组成的网格中，△ABC 的三个顶点均在格点上，则 sin∠ABC 的值为 ．

11. 如图，在 △ABC 中，DE∥BC，DE 分别与 AB，AC 相交于点 D，E，若 AD=2，DB=1，S△ADE=4，则 S△ABC 的值为 ．

12. 掷一枚质地均匀的正方体骰子，骰子的六个面上分别有 1 到 6 的点数，掷得面朝上的点数为偶数的概率为 ．

13. 半径为 2 的圆中，60∘ 的圆心角所对的弧的弧长为 ．

14. 二次函数 y=ax2+bx+ca≠0 的图象如图所示，那么一元二次方程 ax2+bx+c=m（a≠0，m 为常数且 m≤4）的两根之和为 ．

15. “割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣”这是我国古代著名数学家刘徽在《九章算术注》中提到的“如何求圆的周长和面积”的方法，即“割圆术”“割圆术”的主要意思是用圆内接正多边形去逐步逼近圆．刘徽从圆内接正六边形出发，将边数逐次加倍，并逐次得到正多边形的周长和面积．如图，AB 是圆内接正六边形的一条边，半径 OB=1，OC⊥AB 于点 D，则 AB 的长为 ，圆内接正十二边形的边 BC 的平方是 ．

16. 数学课上，老师提出如下问题：△ABC 是 ⊙O 的内接三角形，OD⊥BC 于点 D．请借助直尺，画出 △ABC 中 ∠BAC 的平分线．
晓龙同学的画图步骤如下：
（1）延长 OD 交 BC 于点 M；
（2）连接 AM 交 BC 于点 N．
所以线段 AN 为所求 △ABC 中 ∠BAC 的平分线．
请回答：晓龙同学画图的依据是 ．

三、解答题（共12小题；共156分）
17. 计算：tan45∘+27−2−20180−4cs30∘．

18. 如图，△ABC 在方格纸中．
（1）请在方格纸上建立平面直角坐标系 xOy，使 A2,3，C4,2，并写出 B 点坐标；
（2）以原点 O 为位似中心，相似比为 2，在第一象限内将 △ABC 放大，画出放大后的图形 △AʹBʹCʹ．

19. 已知二次函数 y=x2−2x−3．
（1）用方法将 y=x2−2x−3 化成 y=ax−h2+k 的形式．
（2）在平面直角坐标系 xOy 中画出该函数的图象（不用列表）．
（3）当 0≤x≤3 时，y 的取值范围是 ．

20. 在某一电路中，电源电压 U 保持不变，电流 IA 与电阻 RΩ 之间的函数关系如图所示．
（1）求 I 与 R 之间的函数解析式；
（2）结合图象直接写出当电路中的电流不超过 12 A 时，电路中电阻 R 的取值范围是 ．

21. 如图，已知 AB 为 ⊙O 的直径，PA，PC 是 ⊙O 的切线，A，C 为切点，∠BAC=30∘．
（1）求 ∠P 的大小；
（2）若 AB=6，求 PA 的长．

22. 从共享单车，共享汽车等共亨出行到共享充电宝，共亨雨伞等共享物品，各式各样的共经济模式在各个领域迅速普及应用，越来越多的金业与个人成为参与者与受益者、小宇和小强分别对共享经济中的“共享出行”“和“共享知识”最感兴趣，他们上网查了相关资料，顺便收集到四个共享经济领域的图标，并将其制成编号为，A，B，C，D的四张卡片（除编号和内容外，其余完全相同），他们将这四张卡片背面朝上，洗匀放好，从中随机抽取一张不放回，再从中随机抽取一张，请用列表或画树状图的方法，求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率．（这四张卡片分别用它们的编号A，B，C，D表示）

23. 为了维护国家主权和海洋权利，海监部门对我国领海实现了常态化巡航管理，如图，正在执行巡航任务的海监船以每小时 50 海里的速度向正东方航行，在 A 处测得灯塔 P 在北偏东 60∘ 方向上，继续航行 1 小时到达 B 处，此时测得灯塔 P 在北偏东 30∘ 方向上．
（1）∠APB= ；
（2）已知在灯塔 P 的周围 25 海里内有暗礁，问海监船继续向正东方向航行是否安全?

24. 在平面直角坐标系 xOy 中，反比例函数 y=mx 的图象过点 A6,1．
（1）反比例函数的表达式为 ．
（2）若一次函数 y=kx 过点 A，则不等式 kx>mx 的解集为 ．
（3）过点 A 的直线与反比例函数 y=mx 图象的另一个交点为 B，与 y 轴交于点 P，若 AP=3PB，求点 B 的坐标．

25. 己知：如图，在 △ABC 中，AB=AC，以 C 为直径作 ⊙O 交 BC 于点 D，过点 D 作 ⊙O 的切线交 AB 于点 E，交 AC 的延长线于点 F．
（1）求证：DE⊥AB；
（2）若 tan∠BDE=12，CF=3，求 DF 的长．

26. 如图，在四边形 ABCD 中，AD∥BC，∠ADC=90∘，点 E 是 BC 边上一动点，连接 AE，过点 E 作 AE 的垂线交直线 CD 于点 F．已知 AD=4 cm，CD=2 cm，BC=5 cm，设 BE 的长为 x cm，CF 的长为 y cm．小东根据学习函数的经验，对函数 y 随自变量 x 的变化而变化的规律进行探究．下面是小东的探究过程，请补充完整：
（1）通过取点、画图、测量，得到了 x 与 y 的几组值，如下表：
（说明：补全表格时相关数据保留一位小数）
（2）建立直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象．
（3）结合画出的函数图象，解决问题：当 BE=CF 时，BE 的长度约为 cm．

27. 在平面直角坐标系 xOy 中，抛物线 y=nx2−4nx+4n−1n≠0，与 x 轴交于点 C，D（点 C 在点 D 的左侧），与 y 轴交于点 A．
（1）求抛物线顶点 M 的坐标．
（2）若点 A 的坐标为 0,3，AB∥x 轴，交抛物线于点 B，求点 B 的坐标．
（3）在（2）的条件下，将抛物线在 B，C 两点之间的部分沿 y 轴翻折，翻折后的图象记为 G，若直线 y=12x+m 与图象 G 有一个交点，结合函数的图象，求 m 的取值范围．

28. 已知边长为 2a 的正方形 ABCD，对角线 AC，BD 交于点 Q，对于平面内的点 P 与正方形 ABCD，给出如下定义：如果 a≤PQ≤2a，则称点 P 为正方形 ABCD 的“关联点”．
在平面直角坐标系 xOy 中，若 A−1,1，B−1,−1，C1,−1，D1,1．
（1）在 P1−12,0，P212,32，P30,2 中，正方形 ABCD 的“关联点”有 ．
（2）已知点 E 的横坐标是 m，若点 E 在直线 y=3x 上，并且 E 是正方形 ABCD 的“关联点”，求 m 的取值范围．
（3）若将正方形 ABCD 沿 x 轴平移，设该正方形对角线交点 Q 的横坐标是 n，直线 y=3x+1 与 x 轴，y 轴分别相交于 M，N 两点．如果线段 MN 上的每一个点都是正方形 ABCD 的“关联点”，求 n 的取值范围
答案
第一部分
1. C【解析】根据反比例函数的概念可知，y=kxk≠0，则 k=x⋅y，
根据图象信息得，图象过点 1,−2，则 k=k−2=−2，
则 y=−2x．
2. B【解析】连接 CO．
∵AB 为 ⊙O 的直径，AB=14，BC=7，
∴△BCO 为等边三角形，
∴∠BOC=60∘，
∴∠BDC=12∠BOC=30∘．
3. B【解析】设扇形的半径为 R，由题意：3π=120π⋅R2360，
解得 R=±3，
∵ R>0，
∴ R=3 cm，
∴ 这个扇形的半径为 3 cm．
4. B【解析】以原点 O 为位似中心，把线 AB 放大后得到线段 CD．
∵B2,0，D5,0，
∴OBOD=25．
∵A1,2，
∴B52,5．
5. D
6. A
7. A【解析】过点 C 作 CE⊥x 轴于点 E，过点 D 作 DF⊥x 轴于点 F，如图所示．
设 BD=a，则 OC=3a．
∵△AOB 为边长为 6 的等边三角形，
∴∠COE=∠DBF=60∘，OB=6．
在 Rt△COE 中，∠COE=60∘，∠CEO=90∘，OC=3a，
∴∠OCE=30∘，
∴OE=32a，CE=OC2−OE2=332a，
∴ 点 C32a,332a．
同理，可求出点 D 的坐标为 6−12a,32a．
∵ 反比例函数 y=kxk≠0 的图象恰好经过点 C 和点 D，
∴k=32a×332a=6−12a×32a，
∴a=65，k=81325．
8. B
第二部分
9. y=−1x（答案不唯一）
【解析】由题可知：k<0，
∴ 可令 k=−1．
故反比例函数可为 y=−1x．
10. 31010
【解析】∵BC=12+32=10 ，
∴sin∠ABC=310=31010．
11. 36
【解析】∵DE∥BC，
∴△ADE∽△ABC，
∵AD=2，DB=1，
∴AB=3，
∴S△ADES△ABC=ADAB2=19，
∴S△ABC=9S△ADE=9×4=36．
12. 12
13. 2π3
【解析】∵ 圆的半径为 2，
∴60∘ 的圆心角所对的弧的弧长为 60×2π180=2π3．
14. −2
15. 1，2−3
【解析】∵AB 是圆内接正六边形的一条边，
∴∠AOB=60∘，
∵OA=OB，
∴△AOB 为等边三角形，
∴AB=OB=1，
∵OC⊥AB，
∴DA=DB=12AB=12，
由勾股定理可得：OD=OB2−BD2=32，
∴CD=OC−OD=1−32，
∴BC2=BD2+CD2=122+1−322=2−3．
16. 垂径定理，等弧所对的圆周角相等
第三部分
17. tan45∘+27−2−20180−4cs30∘=1+33−1−4×32=3.
18. （1） B5,4．
（2） 如图：
19. （1） y=x2−2x−3=x2−2x+1−4=x−12−4．
（2） 如下图：
（3） −4≤y≤0
【解析】由图象可知，当 x=1 时，y 有最小值 ymin=−4，
当 x=3 时，y 有最大值，ymax=0，
∴ 当 0≤x≤3 时，−4≤y≤0．
20. （1） 设 I=UR，代入 A6,6，则 6=U6，
∴U=36，
∴I=36R．
（2） R≥3 Ω
【解析】令 I=12 A，则 R=3612=3 Ω，
∴ 电流不超过 12 A 时，电阻 R 的取值范围为 R≥3 Ω．
21. （1） ∵PA，PC 是 ⊙O 的切线，A，C 为切点，
∴OA⊥AP，PA=PC，
∴∠PAC=60∘，
∴∠P=60∘．
（2） PA=AC=32AB=33．
22. 共有 12 种可能，每种可能概率相同，其中抽出A和D共有 12 种可能，
∴ 概率为 P=212=16．
23. （1） 30∘
【解析】作 PQ⊥AB 于点 Q，
∴∠APQ=60∘，∠BPQ=30∘，
∴∠APB=∠APQ−∠BPQ=30∘．
（2） 设 BQ=x 海里，在 Rt△BPQ 中，PQ=3BQ=3x 海里，
由（1）知 ∠APB=30∘=∠PAB，
∴AB=50 海里，
∴x=25，
∴PQ=3x=253 海里 >25 海里．
∴ 海监船继续向正东方向航行安全．
24. （1） y=6x
【解析】将 A6,1 代入 y=mx 中，得 m=6．
∴y=6x．
（2） −66
【解析】一次函数 y=kx 与 y=6x 均过点 A6,1，
由中心对称可得另一交点为 −6,−1，
由图象可知：kx6．
（3） 如图①，作 AM，B1N⊥y 轴于点 M，N．
∴AM∥BN，
∴△AMP1∽△B1NP1，
∵AM=6，即 P1A=3P1B1，
∴B1N=2，
∴xB1=−2，
∴yB1=−3，
∴B1−2,−3．
如图②作 AQ，B2T⊥y 轴于点 Q，T．
∴AQ∥B2T，
∴△AQP2∽B2TP2，
∵AQ=6，P2A=3P2B2，
∴B2T=2，
∴xB2=2，
∴yB2=3．
∴B22,3．
∴ 点 B 的坐标为 2,3 或 −2,−3．
25. （1） 连接 OD．
∵OC=OD，
∴∠OCD=∠ODC，
∵AB=AC，
∴∠B=∠ACB，
∴∠B=∠ODC，
∴AB∥OD．
∵DE 于 ⊙O 相切，OD 为半径，
∴OD⊥DE，
∴DE⊥AB．
（2） 方法一：连接 AD．
∵AC 为 ⊙O 直径，
∴∠ADC=90∘，
∴∠BDE=∠BAD，
∵tan∠BDE=12，
设 BE=a，则 DE=2a，AE=4a，
∴AB=AC=5a，
∴OA=OC=OD=12AC=52a，
∴OF=OC+CF=52a+3，AF=AC+CF=5a+3．
由（1）知，OD∥AB，
∴△ODF∽△AEF，
∴ODAE=OFAF=DFEF，
∴52a4a=52a+35a+3，解得 a=95．
∴DFDF+2a=52a4a，
∴DF=6．
【解析】方法二：连接 AD．
∵AC 为 ⊙O 直径，
∴∠ADC=90∘，
∵AB=AC，
∴∠BAD=∠CAD，
∵∠BDE=∠BAD，∠BDE=∠CDF，
∴∠CDF=∠CAD，
∵∠F=∠F，
∴△FCD∽△FDA，
∴FCFD=CDAD，
∵tan∠CAD=CDAD=tan∠BDE=12．
∴FD=2FC=6．
26. （1） 1.5
（2） 如图．
（3） 0.7（0.6−0.8 均可以）
27. （1） M2,−1．
（2） B4,3．
（3） ∵ 抛物线 y=nx2−4nx+4n−1n≠0 与 y 轴交于点 A0,3，
∴4n−1=3．
∴n=1．
∴ 抛物线的表达式为 y=x2−4x+3．
由 12x+m=x2+4x+3．
由 Δ=0，得：m=−116．
∵ 抛物线 y=x2−4x+3 与 x 轴的交点 C 的坐标为 1,0，
∴ 点 C 关于 y 轴的对称点 C1 的坐标为 −1,0．
把 −1,0 代入 y=12x+m，得：m=12．
把 −4,3 代入 y=12x+m，得：m=5．
∴ 所求 m 的取值范围是 m=−116 或 1228. （1） P2，P3
【解析】由题意正方形 ABCD 的“关联点”中正方形的内切圆和外切圆之间（包括两个圆上的点），
观察图象可知：正方形 ABCD 的“关联点”为 P2，P3．
（2） 作出正方形 ABCD 的内切圆和外接圆，
∴OF=1，OG=2．
∵E 是正方形 ABCD 的“关联点”，
∴E 在正方形 ABCD 的内切圆和外接圆之间，
∵ 点 E 在直线 y=3x 上，
∴ 点 E 在线段 FG 上．
分别做 FFʹ⊥x 轴，GGʹ⊥x 轴，
∵OF=1，OG=2，
∴OFʹ=12，OGʹ=22．
∴12≤m≤22．
根据对称性，可以得出 −22≤m≤−12．
∴12≤m≤22，−22≤m≤−12．
（3） ∵M−33,0，N0,1，
∴OM=33，ON=1．
∴OMN=60∘．
∵ 线段 MN 上的每一个点都是正方形 ABCD 的“关联点”，
① MN 与小 ⊙Q 相切于点 F，如图：
∵QF=1，∠OMN=60∘，
∴QM=233．
∵OM=33，
∴OQ=33．
∴Q133,0．
② M 落在大 ⊙Q 上，如图：
∵QM=2，OM=33，
∴OQ=2−33．
∴Q22−33,0．
综上：33≤n≤2−33．