初中数学人教版八年级上册13.3.2 等边三角形教案

这是一份初中数学人教版八年级上册13.3.2 等边三角形教案，共4页。教案主要包含了情境引入，探究新知，当堂训练，小结归纳，作业设计等内容，欢迎下载使用。
年 级
八年级
课题
12.3.2等边三角形（1）
课型
新授
教 学 媒 体
多 媒 体
教
学
目
标
知识技 能
1. 掌握并会运用等边三角形的性质.
2. 掌握并会运用等边三角形的判定.
过程方 法
经过应用等边三角形的性质与判定的过程培养学生分析问题、解决问题的能力.
情感态 度
经过应用等边三角形的性质与判定的过程增强学生挑战困难的勇气，体会成功的喜悦，增强学习的信心.
教学重点
等边三角形的性质和判定.
教学难点
等边三角形的性质的应用.
教 学 程 序 及 教 学 内 容
师生行为
设计意图
一、情境引入
在一次探究活动中，老师给同学们出了一道题目：“如果等腰三角形有一个角是60°，那么这个三角形的三边有什么关系？”。
小明假设底角为60°，得出了三个角都是60°，小亮假设顶角为60°，也得出了三个角都是60°，根据“等角对等边”，最后得出结论：三边都相等.
老师告诉他们“这种三条边都相等的叫做等边三角形”。小明、小亮也发表了自己的看法，小明认为“三条边都相等的三角形是等边三角形，而不是等腰三角形”；小亮认为“等边三角形也还是等腰三角形，只是比一般的等腰三角形特殊而已”.， 小明、小亮谁说的有道理呢？学完这节课就能见分晓。
二、探究新知
探究：
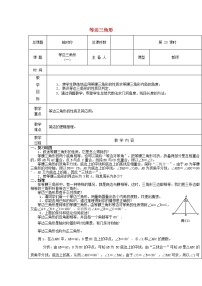
观察右图，回答下面的问题
等边三角形边、角具有什么性质？
在△ABC中，∠A=∠B=∠C，你能得到AB=BC=CA吗？为什么？
在△ABC中，AB=BC，∠A=60°（ ∠B=60°或
∠C =60°）你能得到AB=BC=CA吗？为什么？
等边三角形是轴对称图形吗？有几条对称轴？
等边三角形与等腰三角形有什么关系呢？
归纳等边三角形的性质：
等边三角形的三个内角都相等，并且每一个内角都等于60°。
等边三角形的判定：
三个角都相等的三角形是等边三角形。
有一个角是60°的等腰三角形是等边三角形。
【例题】如图，已知、均为等边三角形，且B、C、E在一条直线上，连结BD、AE分别交AC、DC于F、G.
(1) 求证：AE=BD；
(2) 求证：CF=CG；
(3)连结FG，求证：
为等边三角形.
【分析】（1）由于等边三角形各边都相等，各角都是60°，不难证明，所以AE＝BD；
（2）利用（1）中的全等，不难证明，所以CF=CG；
（3）因为等腰三角形，只须证其有60°角。
【点拨】本题条件中，即使B、C、E不在一条直线上，所证线段依然相等，只是为一般等腰三角形，请同学们自己验证。
三、当堂训练
1. 对于等边三角形，下列说法不成立的是（ ）
A．三条边都相等 B．每个角都是60°
C．有三条对称轴 D．两条高互相垂直
2．下列说法中正确的个数是（ ）
①有三条对称轴的三角形是等边三角形；
②三个外角都相等的三角形是等边三角形；
③有一个外角为120°的等腰三角形是等边三角形；
④腰上的高与底边上的高相等的等腰三角形是等边三角形。
A．1 B．2 C．3 D．4
3．等腰三角形的腰长为2，顶角与底角相等，则这个等腰三角形的周长为（ ）
A．4 B．5 C．6 D．无法确定
4．若等腰三角形的腰长为2，顶角大于底角，则这个等腰三角形的周长为（ ）
A．6 B．大于6 C．小于6 D无法确定
5．如图，已知等边中，BD=CE，AD与BE交于点P，求∠APE的度数.
6．已知、都是等边三角形.
求证：AE=CD.
7．如图所示，E是等边中AC边上的点，BE=CD，∠1=∠2.
求证：为等边三角形.
8．在中，∠ACB=90°，、都是等边三角形，请你探究EC与AD的位置关系，并证明你的结论.
拓展思维：
如图，延长的各边，使得BF=AC，AE=CD=AB，顺次连接D、E、F，得到
为等边三角形。
求证：（1）≌
（2）为等边三角形.
四、小结归纳
学生本节课的主要收获
1. 掌握等边三角形的性质。
2. 掌握等边三角形的判定。
五、作业设计
1. 教材第57页习题第11题。
2. 教材第65页习题第12题。
3. 教材第66页习题第14题。
教师展示问题，板书课题。
。
学生观察图形，回答问题。

教师给出性质、判定的准确描述，并板书性质、判定。
（1）、（2）教师引导学生根据图形选择恰当的方法证明两条线段相等。（3）教师引导学生选择恰当的判定方法证明等边三角形。
学生相互交流、相互讨论解决问题。
学生独立思考，自己解决问题。
学生独立思考，自己解决问题。
第3、4题学生画图、比较，体会前后图形底边的变化，然后选择答案。
学生先独立思考，在相互交流。
教师引导学生把外角∠APE转化。
学生观察图形，选择恰当的方法证明两条线段相等。
学生先独立思考，在相互交流。
教师引导学生证出
△ABE≌△ACD。
学生先独立思考，在相互交流，通过观察、画图猜出结论。
教师引导学生延长
EC。
（1）教师引导学生证出运用等式的性质证出AF=CE。
（2）教师引导学生
运用恰当的方法判定等边三角形。
教师引导学生回顾本节课知识，并总结、归纳本节课的重点。
通过情境引入本节课课题，增加学生的学习兴趣。
学生通过观察、思考、证明、归纳，培养学生的语言表达能力、观察能力、归纳能力、养成良好的自觉探索几何命题的习惯。
巩固等边三角形性质与判定。培养学生合作意识及分析问题、解决问题的能力。
考察学生对等边三角形性质的掌握。
考察学生对等边三角形判定的掌握。
考察学生对等边三角形判定的掌握，培养学生的动手能力。
考察学生对等边三角形性质的掌握，体会数学中转化的思想。
考察学生对等边三角形性质的掌握。
考察学生对等边三角形性质、判定的掌握。培养学生分析问题、解决问题的能力。
考察学生对等边三角形性质的掌握，知道等腰三角形的“三线合一”对等边三角形也适用。
培养学生大胆尝试，勇于探索，提高学生的思维能力和证明能力。
一、等边三角形的性质。 三、、例题解析。
二、等边三角形的判定。 拓展思维解析。

教学反思