

还剩19页未读,
继续阅读
2021年重庆市北碚区西南大学附属中学校中考数学仿真押题试卷(八)
展开
这是一份2021年重庆市北碚区西南大学附属中学校中考数学仿真押题试卷(八),共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
1下列各数中,比﹣3小的数是( )
A.0B.﹣2C.|﹣3|D.﹣4
2成渝历来地理相近,文化相亲,下列成渝文化标志可以抽象成轴对称图形的是( )
A.B.
C.D.
3下列运算正确的是( )
A.a9÷a3=a3B.(a3)3=a6
C.(﹣2a3)2=4a6D.(1﹣2a)2=4a2﹣2a+1
4如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠ACE=20°,则∠BDE的度数为( )
A.90°B.100°C.110°D.120°
5如图,在△ABC中,点A的坐标为(3,6),以原点O为位似中心,将△ABC位似缩小后得到△A′B′C′.若点A′的坐标为(1,2),△A′B′C′的面积为1,则△ABC的面积为( )
A.2B.3C.4D.9
6按如图所示的运算程序,若输出结果为y=5,则输入的值可以是( )
A.3B.6C.﹣3或6D.﹣3或1或6
7《九章算术)中有这样一个题:“今有五雀、六燕,集称之衡,雀俱重,燕俱轻,一雀一燕交而处,衡适平.并燕、雀重一斤.问燕、雀一枚各重几何?”译文:“今有5只雀、6只燕,分别放在一起而且用称称重,5只雀总重量比6只燕的总重量要重、若交换一只雀、一只燕,它们重量相等,5只雀,6只燕重量为1斤.问每1只雀、燕各重多少斤?”设每一只雀的重量为x斤,每一只燕的重量为y斤,则可建立方程组为( )
A.B.
C.D.
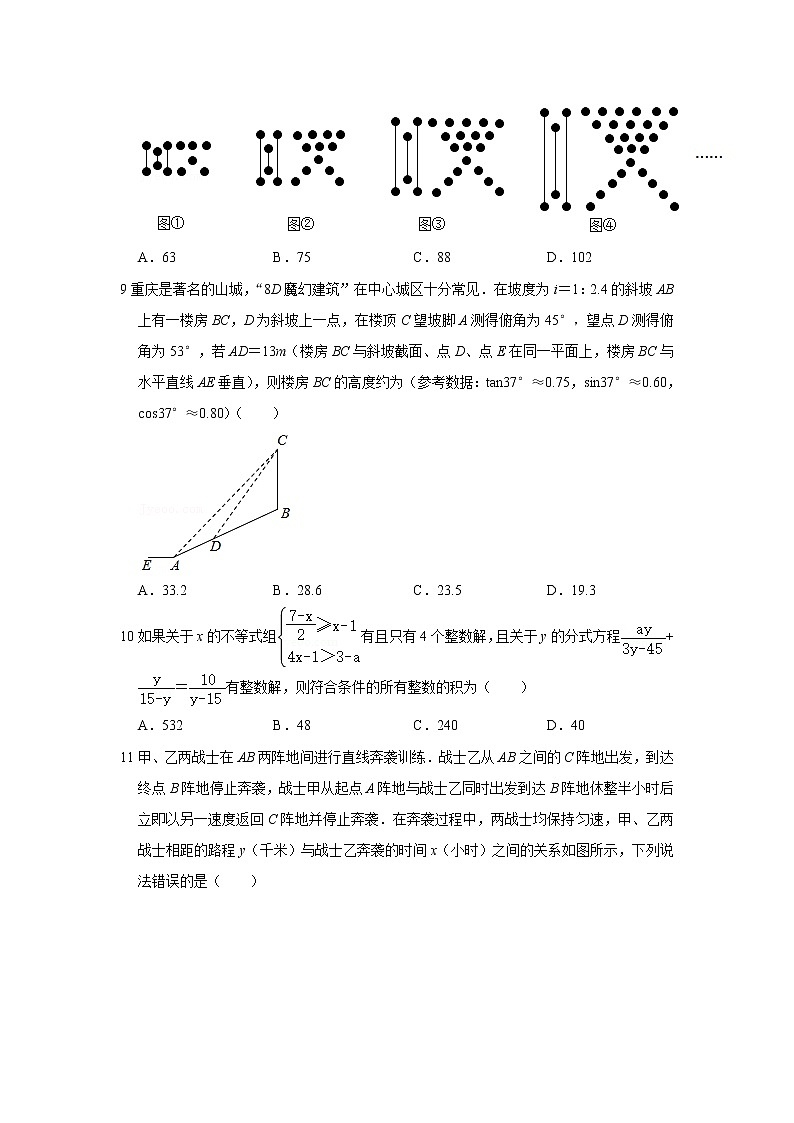
8汉字文化正在走进人们的日常消费生活.下列图形都是由同样大小的圆点和线段按照一定的规律排列组成的篆书简化“汉”字,其中,图①中共有12个圆点,图②中共有18个圆点,图③中共有25个圆点,图④中共有33个圆点…依此规律则,图⑧中共有圆点的个数是( )
A.63B.75C.88D.102
9重庆是著名的山城,“8D魔幻建筑”在中心城区十分常见.在坡度为i=1:2.4的斜坡AB上有一楼房BC,D为斜坡上一点,在楼顶C望坡脚A测得俯角为45°,望点D测得俯角为53°,若AD=13m(楼房BC与斜坡截面、点D、点E在同一平面上,楼房BC与水平直线AE垂直),则楼房BC的高度约为(参考数据:tan37°≈0.75,sin37°≈0.60,cs37°≈0.80)( )
A.33.2B.28.6C.23.5D.19.3
10如果关于x的不等式组有且只有4个整数解,且关于y的分式方程+=有整数解,则符合条件的所有整数的积为( )
A.532B.48C.240D.40
11甲、乙两战士在AB两阵地间进行直线奔袭训练.战士乙从AB之间的C阵地出发,到达终点B阵地停止奔袭,战士甲从起点A阵地与战士乙同时出发到达B阵地休整半小时后立即以另一速度返回C阵地并停止奔袭.在奔袭过程中,两战士均保持匀速,甲、乙两战士相距的路程y(千米)与战士乙奔袭的时间x(小时)之间的关系如图所示,下列说法错误的是( )
A.战士乙奔袭的速度为每小时40千米
B.战士甲到达B阵地的时间为7小时
C.战士甲返回C阵地比战士乙到B阵地时间晚3小时
D.战士甲全程共行驶了840千米
12如图,在平面直角坐标系中,等腰△ABC底边BC的中点D的坐标为(﹣1,0),顶点C的坐标为(0,﹣3),双曲线y=与线段AB交于点E,与AC交于点F,且点E,F分别为AB,AC的中点,则k的值为( )
A.﹣B.﹣C.﹣D.﹣
二、填空题:(本大题共6个小题,每小题4分,共24分)请将每小题的答案直接填在答题卡中对应的横线上
13据媒体报道,上海微电子装备(集团)股份有限公司宣布在2021年至2022年交付国产第一台28nm的沉浸式光刻机.28纳米可换算为0.000000028米,数据0.000000028用科学记数法表示为 .
14计算:cs60°﹣π0+(﹣)﹣2= .
15现有3张正面分别标有数字﹣1,1,2的不透明卡片,它们除数字外其余完全相同,将它们背面朝上洗均匀,随机抽取一张,并记下数字m,不放回,再随机抽取一张记下数字n,则二次函数y=mx2+nx的对称轴在y轴左侧的概率是 .
16如图,正方形ABCD的边长为6,以点D为圆心,4为半径作圆弧于正方形的边相交,则图中由圆弧和正方形的边围成的阴影部分的面积为 .(结果保留π)
17如图,在△ABC中,∠ACB=90°,AC=4,BC=3,E是AB的中点.将△ABC沿着直线BC翻折,得到△DBC,再将△CAE沿着直线CE翻折,得到△CFE,G为CD的中点,连接FG,则线段FG的长等于 .
18新世纪百货推出A,B,C三种零食大礼包,每种礼包都由一定数量的坚果、牛肉干和薄脆饼组合搭配构成.三种大礼包的成本分别为礼包中三种零食的成本之和,同种零食的单价相同.已知2袋牛肉干和5袋薄脆饼的价格相同,一份A礼包包含6袋坚果、4袋牛肉干和2袋薄脆饼,一份B礼包包含4袋坚果、6袋牛肉干和4袋薄脆饼.若一份B,C礼包的成本相同,均比一份A礼包的成本贵40%,一份C礼包中的零食袋数与一份A礼包中的零食袋数之比为3:2,且一份C礼包中坚果袋数比牛肉干袋数多,则一份C礼包中的薄脆饼袋数比牛肉干袋数少 袋.
三、解答题:(本大题共7个小题,每小题10分,共70分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上
19化简:
(1)(x﹣y)2﹣y(x﹣2y);
(2)(a+)÷.
20如图,在△ABC中,BC=3+,∠B=60°,∠C=45°.
(1)用尺规作图的方法作出∠B的角平分线;(保留作图痕迹,不写作法)
(2)若(1)中的角平分线交AC于点D,求△BDC的面积.
21为庆祝中国共产党建党100周年,某学校组织全校学生参加青少年党史知识竞赛,老师从全校学生中随机抽取了男、女同学各40名,并将数据进行整理分析,得到了如下信息:
①女生成绩扇形统计图和男生成绩频数分布直方图如图所示.
(数据分组为A组:x<70,B组:70≤x<80,C组:80≤x<90,D组:90≤x≤100)
②女生C组中全部15名学生的成绩为:86,87,81,83,89,84,85,87,86,89,82,88,89,85,89.
③两组数据的相关统计数据如下表(单位:分)
(1)扇形统计图中A组学生对应的圆心角α的度数为 度,认真分析以上数据信息后填空:中位数b= ,众数c= .
(2)通过以上的数据分析你认为 (填“女生”或“男生”)知识竞赛成绩更好,并说明理由.
(3)若成绩在90分(包含90分)以上为优秀,请你估计我校2400名学生此次知识竞赛中优秀的人数.
22香椿是大家非常喜欢的时令蔬菜,3月份是香椿上市的旺季.某蔬菜超市销售香椿,第一周每千克香椿的销售单价比第二周销售单价高10元,该蔬菜超市这两周共销售香椿180千克,且第一周香椿的销量与第二周的销量之比为4:5,该蔬菜超市这两周香椿销售总额为11600元.
(1)第二周香椿销售单价是每千克多少元?
(2)随着香椿的大量上市,3月份第三周,香椿定价与第二周保持一致,且该蔬菜超市推出会员优惠活动,所有的会员均可享受a%的价格优惠,而非会员需要按照原价购买,第三周香椿的销量比第二周增加了a%,其中通过会员优惠活动购买的销量占第三周香椿总销量的,而第三周香椿的销售总额比第二周销售额提高了a%,求a的值.
23探究函数性质时,我们经历了列表、描点、连线画出函数图象,观察分析图象特征,概括函数性质的过程结合已有的学习经验,请画出函数y=|x﹣|的图象并探究该函数的性质.
(1)列表如下:
写出表中a,b的值:a= ,b= ,c= ;
(2)描点、连线,在所给的平面直角坐标系中画出该函数的图象,观察函数图象,写出该函数的一条性质:
;
(3)结合你所画的函数图象,直接写出不等式组|x﹣|≥x+2的解(保留一位小数,误差不超过0.2).
24在数的学习过程中,我们总会对其中一些具有某种特性的数充满好奇,如学习自然数时,我们发现一种特殊的自然数﹣﹣“三牛数”.
定义1:对于四位自然数n,若千位数字为6,各个数位数字均不为0,n能被6整除,且数n的各个数位数字之和也恰好能被6整除,则称这个自然数n为“三牛数”.
例如:6174是“三牛数”,因为6174÷6=1029,且(6+1+7+4)÷6=3;6834不是“三牛数”,因为6834÷6=1139,但6+8+3+4=21不能被6整除.
定义2:将任意一个“三牛数”n的前两位数字与后两位数字交换,交换后得到一个新的四位数n′,规定:T(n)=.
(1)判断6342,6738是否为“三牛数”,并说明理由;
(2)若n是一个“三牛数”,它的百位数字比十位数字的2倍小2,求T(n)的最大值.
25如图,已知抛物线y=ax2+bx﹣4与x轴交于A,B两点,与y轴交于点C,且点A的坐标为(﹣2,0),直线BC的解析式为y=x﹣4.
(1)求抛物线的解析式.
(2)如图1,过点A作AD∥BC交抛物线于点D(异于点A),P是直线BC下方抛物线上一点,过点P作PQ∥y轴,交AD于点Q,过点Q作QR⊥BC于点R,连接PR.求△PQR面积的最大值及此时点P的坐标.
(3)如图2,点C关于x轴的对称点为点C′,将抛物线沿射线C′A的方向平移2个单位长度得到新的抛物线y′,新抛物线y′与原抛物线交于点M,原抛物线的对称轴上有一动点N,平面直角坐标系内是否存在一点K,使得以D,M,N,K为顶点的四边形是矩形?若存在,请直接写出点K的坐标;若不存在,请说明理由.
四、解答题:(本大题1个小题,共8分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上
26如图,在正方形ABCD中,E,F分别是边BC,AB上一动点,且AF=BE,连接DF,AE交于点G,连接CG.
(1)如图1,若CG=AD,求证:CE=AD;
(2)如图2,当点E,F分别在边BC,AB上运动时,在以GC为斜边构造等腰直角△CGH,连接DH,猜想∠HDG的大小是否为定值,并证明你的结论;
(3)如图3,在(2)的条件下,连接BH,当BH取得最小值时,请直接写出的值.
答案
一、选择题:(本大题共12个小题,每小题4分,共48分)在每个小题的下面都给出了代号为A、B、C、D的四个答案其中只有一个是正确的,请将答题卡上题号右侧正确答案所对应的方框涂黑
1:D.
2:C.
3:C.
4:C.
5:D.
6:D.
7:C.
8:B.
9:D.
10:B.
11:D.
12:A.
二、填空题:(本大题共6个小题,每小题4分,共24分)请将每小题的答案直接填在答题卡中对应的横线上
13:2.8×10﹣8.
14:3.
15:.
16 .36﹣12﹣4π.
17 ..
18:1.
三、解答题:(本大题共7个小题,每小题10分,共70分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上
19
解:(1)(x﹣y)2﹣y(x﹣2y)
=x2﹣2xy+y2﹣xy+2y2
=x2﹣3xy+3y2;
(2)(a+)÷
=
=
=
=.
20
解:(1)如图,BD为所作;
(2)过D点作DE⊥BC于E,如图,
∵BD平分∠ABC,
∴∠DBC=∠ABC=×60°=30°,
设CE=x,
∵∠C=45°,
∴DE=CE=x,
在Rt△BDE中,BE=DE=x,
∵BC=3+,
∴x+x=3+,解得x=,
∴△BDC的面积=×(3+)×=.
21
解:(1)女生C组所占的百分比为:15÷40=37.5%,
360°×(1﹣37.5%﹣40%﹣20%)=9°,
中位数落在C组,将成绩从小到大排列处在第20、21位的两个数的平均数为=88.5,因此中位数b=88.5;
A组人数为:40×(1﹣37.5%﹣40%﹣20%)=1(人),
B组人数为:40×20%=8(人),
C组人数为:15(人),出现次数最多的是89,共4个,
D组人数为:40×40%=16(人),得100分的有40×25%=10个,
故众数c=100,
故答案为:9,88.5,100;
(2)女生的知识竞赛成绩更好,
理由:∵男生和女生的平均数相等,但女生的中位数和满分率都高于男生,
∴女生的知识竞赛成绩更好;
(3)估计该校2400名学生此次考试中优秀的人数2400×=870(名).
答:估计我校2400名学生此次知识竞赛中优秀的人数是870名.
22
解:(1)设第一周香椿销售单价是每千克x元,第二周香椿销售单价是每千克y元,
依题意得:,
解得:.
答:第二周香椿销售单价是每千克60元.
(2)依题意得:60(1﹣a%)×180×(1+a%)×+60×180×(1+a%)×(1﹣)=60×180×(1+a%),
令m=a%,则原方程可变形为5000m2﹣700m=0,
解得:m1=0.14,m2=0(不合题意,舍去).
又∵m=a%,
∴a=14.
答:a的值为14.
23
解:(1)将x=﹣2代入y=|x﹣|,得y=0,
将x=2代入y=|x﹣|,得y=0,
将x=3代入y=|x﹣|,得y=,
∴a=0,b=0,c=;
(2)函数图象如下图所示:
(3)令y2=x+2,其图象如图2所示,
由图可知不等式组|x﹣|≥x+2的解是:x≤﹣2.8或﹣1.3≤x≤0或0≤x≤1.2或x≥4.
24
(1)∵6342÷6=1057,(6+3+4+2)÷6=2.5.
∴6342不是“三牛数”.
∵6738÷6=1123,(6+7+3+8)÷6=4.
∴6738是“三牛数”.
(2)设n=,即这个四位数的百位,十位,个位数字分别为a,b,c.
∴n′=.
∴n=×100+,n′=×100+.
∴T(n)==(×100+﹣×100﹣)
=﹣.
当﹣最大时,T(n)最大,此时应该使b尽可能小.
①当b=1时,a=2b﹣2=0.
∴n=,此时6+0+1+c=c+7能被6整除,故c=5.
但6015不能被6整除.
②b=2时,a=2b﹣2=2,此时,n=.
6+2+2+c=10+c能被6整除,取c=2,n=6222.
6222÷6=1037.
∴T(n)的最大值=62﹣22=40.
25
解:(1)∵B点在x轴上,且B点在y=x﹣4上,
∴B(8,0),
∵A(﹣2,0),B(8,0),都在抛物线y=ax2+bx﹣4上,
∴x=﹣2,x=8是方程ax2+bx﹣4=0的两个根,
∴﹣16=﹣,=6,
∴a=,b=﹣,
∴y=x2﹣x﹣4;
(2)∵AD∥BC,直线BC的解析式为y=x﹣4,
∴直线AD的解析式为y=x+1,
过点B作BG⊥AD交点G,
∵QR⊥BC,
∴QR=BG,
在Rt△ABG中,AB=10,tan∠BAG=,
∴BG=2,
设P(m,m2﹣m﹣4),R(n,n﹣4),则Q(m,m+1),
∵QR=2,
∴20=(m﹣n)2+,
∴n﹣m=2,
∴R(m+2,m﹣3),
S△PQR=×(m+1﹣m2+m+4)×2=﹣m2+2m+5=﹣(m﹣4)2+9,
∴当m=4时,S△PQR有最大值9,
∴P(4,﹣6);
(3)∵点C关于x轴的对称点为点C′,
∴C'(0,﹣4),
∴直线AC的解析式为y=2x+4,
∵抛物线沿射线C′A的方向平移2个单位长度,
∴抛物线沿着x轴负方向平移2个单位长度,沿着y轴负方向平移4个单位长度,
∵y=x2﹣x﹣4=(x﹣3)2﹣,
∴y'=(x﹣1)2﹣,
联立(x﹣3)2﹣=(x﹣1)2﹣,解得x=6,
∴M(6,﹣4),
联立x+1=x2﹣x﹣4,解得x=10或x=﹣2,
∵D异于点A,
∴D(10,6),
∵y=x2﹣x﹣4的对称轴为直线x=3,
设N(3,t),K(x,y),
①当DM与KN为矩形对角线时,
DM的中点与KN的中点重合,
∴8=,1=,
∴x=13,t=2﹣y,
∵DM=KN,
∴16+100=(3﹣x)2+(t﹣y)2,
∴y=﹣1或y=3,
∴K(13,﹣1)或K(13,3);
②当DN与MK为矩形对角线时,
DN的中点与MK的中点重合,
∴=,=,
∴x=7,t=y﹣10,
∵DN=MK,
∴49+(6﹣t)2=(6﹣x)2+(y+4)2,
∴y=,
∴K(7,);
③当KD与MN为矩形对角线时,
KD的中点与MN的中点重合
∴=,=,
∴x=﹣1,t=10+y,
∵KD=MN,
∴(x﹣10)2+(6﹣y)2=9+(t+4)2,
∴y=﹣,
∴K(﹣1,﹣);
综上所述:以D,M,N,K为顶点的四边形是矩形时,K点坐标为(﹣1,﹣)或(7,)或(13,﹣1)或(13,3).
四、解答题:(本大题1个小题,共8分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上
26
(1)延长DC、AE相交于点K,如图:
∵四边形ABCD是正方形,
∴AD=BA,∠DAF=90°=∠ABE,
∵AF=BE,
∴△ADF≌△BAE(SAS),
∴∠ADF=∠BAE,
∴∠AFG+∠BAE=∠AFG+∠ADF=90°,
∴DF⊥AE,
∴∠K+∠CDG=90°=∠DGK=∠CGD+∠CGK,
∵CG=CD,
∴∠CDG=∠CGD,
∴∠K=∠CGK,
∴CK=CG=CD=AB,
又∠CEK=∠AEB,∠ECK=∠EBA=90°,
∴△CEK≌△BAE(AAS),
∴CE=BE=BC=AD;
(2)∠HDG=45°;证明如下:
连接AC,如图:
∵四边形ABCD是正方形,
∴CA=CD,∠ACD=45°,
∵等腰直角△HGC,
∴CG=CH,∠GCH=45°,
∴==,∠ACG=∠DCH,
∴△ACG∽△DCH,
∴∠CHD=∠CGA=∠CGH+∠AGD+∠DGH=135°+∠DGH,
∴∠DHG=360°﹣∠CHG﹣∠CHD
=360°﹣90°﹣(135°+∠DGH)
=135°﹣∠DGH,
∵∠DHG=180°﹣∠HDG﹣∠DGH,
∴135°﹣∠DGH=180°﹣∠HDG﹣∠DGH,
∴∠HDG=45°;
(3)过点C作CN⊥DF于点N,取CD的中点M,以DM为斜边在正方形外作等腰Rt△DOM,过点O作OT⊥BC,交BC的延长线于点T,过点H作HL⊥BC于点L,过点O作OS⊥CD于点S,连接OH、MN、OB,
∵∠CDN+∠ADG=90°=∠DAG+∠ADG,
∴∠CDN=∠DAG,
∵∠CND=90°=∠DGA,CD=DA,
∴△CDN≌△DAG(AAS),
∴DN=AG,
由(2)可知:∠GDH=45°,AG=DH,
∴DN=DH,∠GDH=45°=∠MDO,
∴∠NDM=∠HDO,
∵DM=DO,
∴==,
∴△DMN∽△DOH,
∴=,
∵MN是Rt△CDN斜边上的中线,
∴DM=MN,
∴OH=DO=DM=CD,
∵TC=OS=DM=CD,
∴OT=CS=CD,BT=CD,
∴OB==CD,
∴BH≥OB﹣OH=CD,
故当BH取得最小值时,B、H、O共线,
此时由HL∥OT,可得:
==,
即:=,
∴=,
∴==•=.
平均数
中位数
众数
满分率
女生
90
b
c
25%
男生
90
88
98
15%
x
…
﹣5
﹣4
﹣3
﹣2
﹣1
1
2
3
4
5
6
…
y
…
3
a
3
3
b
c
3
…
1下列各数中,比﹣3小的数是( )
A.0B.﹣2C.|﹣3|D.﹣4
2成渝历来地理相近,文化相亲,下列成渝文化标志可以抽象成轴对称图形的是( )
A.B.
C.D.
3下列运算正确的是( )
A.a9÷a3=a3B.(a3)3=a6
C.(﹣2a3)2=4a6D.(1﹣2a)2=4a2﹣2a+1
4如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠ACE=20°,则∠BDE的度数为( )
A.90°B.100°C.110°D.120°
5如图,在△ABC中,点A的坐标为(3,6),以原点O为位似中心,将△ABC位似缩小后得到△A′B′C′.若点A′的坐标为(1,2),△A′B′C′的面积为1,则△ABC的面积为( )
A.2B.3C.4D.9
6按如图所示的运算程序,若输出结果为y=5,则输入的值可以是( )
A.3B.6C.﹣3或6D.﹣3或1或6
7《九章算术)中有这样一个题:“今有五雀、六燕,集称之衡,雀俱重,燕俱轻,一雀一燕交而处,衡适平.并燕、雀重一斤.问燕、雀一枚各重几何?”译文:“今有5只雀、6只燕,分别放在一起而且用称称重,5只雀总重量比6只燕的总重量要重、若交换一只雀、一只燕,它们重量相等,5只雀,6只燕重量为1斤.问每1只雀、燕各重多少斤?”设每一只雀的重量为x斤,每一只燕的重量为y斤,则可建立方程组为( )
A.B.
C.D.
8汉字文化正在走进人们的日常消费生活.下列图形都是由同样大小的圆点和线段按照一定的规律排列组成的篆书简化“汉”字,其中,图①中共有12个圆点,图②中共有18个圆点,图③中共有25个圆点,图④中共有33个圆点…依此规律则,图⑧中共有圆点的个数是( )
A.63B.75C.88D.102
9重庆是著名的山城,“8D魔幻建筑”在中心城区十分常见.在坡度为i=1:2.4的斜坡AB上有一楼房BC,D为斜坡上一点,在楼顶C望坡脚A测得俯角为45°,望点D测得俯角为53°,若AD=13m(楼房BC与斜坡截面、点D、点E在同一平面上,楼房BC与水平直线AE垂直),则楼房BC的高度约为(参考数据:tan37°≈0.75,sin37°≈0.60,cs37°≈0.80)( )
A.33.2B.28.6C.23.5D.19.3
10如果关于x的不等式组有且只有4个整数解,且关于y的分式方程+=有整数解,则符合条件的所有整数的积为( )
A.532B.48C.240D.40
11甲、乙两战士在AB两阵地间进行直线奔袭训练.战士乙从AB之间的C阵地出发,到达终点B阵地停止奔袭,战士甲从起点A阵地与战士乙同时出发到达B阵地休整半小时后立即以另一速度返回C阵地并停止奔袭.在奔袭过程中,两战士均保持匀速,甲、乙两战士相距的路程y(千米)与战士乙奔袭的时间x(小时)之间的关系如图所示,下列说法错误的是( )
A.战士乙奔袭的速度为每小时40千米
B.战士甲到达B阵地的时间为7小时
C.战士甲返回C阵地比战士乙到B阵地时间晚3小时
D.战士甲全程共行驶了840千米
12如图,在平面直角坐标系中,等腰△ABC底边BC的中点D的坐标为(﹣1,0),顶点C的坐标为(0,﹣3),双曲线y=与线段AB交于点E,与AC交于点F,且点E,F分别为AB,AC的中点,则k的值为( )
A.﹣B.﹣C.﹣D.﹣
二、填空题:(本大题共6个小题,每小题4分,共24分)请将每小题的答案直接填在答题卡中对应的横线上
13据媒体报道,上海微电子装备(集团)股份有限公司宣布在2021年至2022年交付国产第一台28nm的沉浸式光刻机.28纳米可换算为0.000000028米,数据0.000000028用科学记数法表示为 .
14计算:cs60°﹣π0+(﹣)﹣2= .
15现有3张正面分别标有数字﹣1,1,2的不透明卡片,它们除数字外其余完全相同,将它们背面朝上洗均匀,随机抽取一张,并记下数字m,不放回,再随机抽取一张记下数字n,则二次函数y=mx2+nx的对称轴在y轴左侧的概率是 .
16如图,正方形ABCD的边长为6,以点D为圆心,4为半径作圆弧于正方形的边相交,则图中由圆弧和正方形的边围成的阴影部分的面积为 .(结果保留π)
17如图,在△ABC中,∠ACB=90°,AC=4,BC=3,E是AB的中点.将△ABC沿着直线BC翻折,得到△DBC,再将△CAE沿着直线CE翻折,得到△CFE,G为CD的中点,连接FG,则线段FG的长等于 .
18新世纪百货推出A,B,C三种零食大礼包,每种礼包都由一定数量的坚果、牛肉干和薄脆饼组合搭配构成.三种大礼包的成本分别为礼包中三种零食的成本之和,同种零食的单价相同.已知2袋牛肉干和5袋薄脆饼的价格相同,一份A礼包包含6袋坚果、4袋牛肉干和2袋薄脆饼,一份B礼包包含4袋坚果、6袋牛肉干和4袋薄脆饼.若一份B,C礼包的成本相同,均比一份A礼包的成本贵40%,一份C礼包中的零食袋数与一份A礼包中的零食袋数之比为3:2,且一份C礼包中坚果袋数比牛肉干袋数多,则一份C礼包中的薄脆饼袋数比牛肉干袋数少 袋.
三、解答题:(本大题共7个小题,每小题10分,共70分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上
19化简:
(1)(x﹣y)2﹣y(x﹣2y);
(2)(a+)÷.
20如图,在△ABC中,BC=3+,∠B=60°,∠C=45°.
(1)用尺规作图的方法作出∠B的角平分线;(保留作图痕迹,不写作法)
(2)若(1)中的角平分线交AC于点D,求△BDC的面积.
21为庆祝中国共产党建党100周年,某学校组织全校学生参加青少年党史知识竞赛,老师从全校学生中随机抽取了男、女同学各40名,并将数据进行整理分析,得到了如下信息:
①女生成绩扇形统计图和男生成绩频数分布直方图如图所示.
(数据分组为A组:x<70,B组:70≤x<80,C组:80≤x<90,D组:90≤x≤100)
②女生C组中全部15名学生的成绩为:86,87,81,83,89,84,85,87,86,89,82,88,89,85,89.
③两组数据的相关统计数据如下表(单位:分)
(1)扇形统计图中A组学生对应的圆心角α的度数为 度,认真分析以上数据信息后填空:中位数b= ,众数c= .
(2)通过以上的数据分析你认为 (填“女生”或“男生”)知识竞赛成绩更好,并说明理由.
(3)若成绩在90分(包含90分)以上为优秀,请你估计我校2400名学生此次知识竞赛中优秀的人数.
22香椿是大家非常喜欢的时令蔬菜,3月份是香椿上市的旺季.某蔬菜超市销售香椿,第一周每千克香椿的销售单价比第二周销售单价高10元,该蔬菜超市这两周共销售香椿180千克,且第一周香椿的销量与第二周的销量之比为4:5,该蔬菜超市这两周香椿销售总额为11600元.
(1)第二周香椿销售单价是每千克多少元?
(2)随着香椿的大量上市,3月份第三周,香椿定价与第二周保持一致,且该蔬菜超市推出会员优惠活动,所有的会员均可享受a%的价格优惠,而非会员需要按照原价购买,第三周香椿的销量比第二周增加了a%,其中通过会员优惠活动购买的销量占第三周香椿总销量的,而第三周香椿的销售总额比第二周销售额提高了a%,求a的值.
23探究函数性质时,我们经历了列表、描点、连线画出函数图象,观察分析图象特征,概括函数性质的过程结合已有的学习经验,请画出函数y=|x﹣|的图象并探究该函数的性质.
(1)列表如下:
写出表中a,b的值:a= ,b= ,c= ;
(2)描点、连线,在所给的平面直角坐标系中画出该函数的图象,观察函数图象,写出该函数的一条性质:
;
(3)结合你所画的函数图象,直接写出不等式组|x﹣|≥x+2的解(保留一位小数,误差不超过0.2).
24在数的学习过程中,我们总会对其中一些具有某种特性的数充满好奇,如学习自然数时,我们发现一种特殊的自然数﹣﹣“三牛数”.
定义1:对于四位自然数n,若千位数字为6,各个数位数字均不为0,n能被6整除,且数n的各个数位数字之和也恰好能被6整除,则称这个自然数n为“三牛数”.
例如:6174是“三牛数”,因为6174÷6=1029,且(6+1+7+4)÷6=3;6834不是“三牛数”,因为6834÷6=1139,但6+8+3+4=21不能被6整除.
定义2:将任意一个“三牛数”n的前两位数字与后两位数字交换,交换后得到一个新的四位数n′,规定:T(n)=.
(1)判断6342,6738是否为“三牛数”,并说明理由;
(2)若n是一个“三牛数”,它的百位数字比十位数字的2倍小2,求T(n)的最大值.
25如图,已知抛物线y=ax2+bx﹣4与x轴交于A,B两点,与y轴交于点C,且点A的坐标为(﹣2,0),直线BC的解析式为y=x﹣4.
(1)求抛物线的解析式.
(2)如图1,过点A作AD∥BC交抛物线于点D(异于点A),P是直线BC下方抛物线上一点,过点P作PQ∥y轴,交AD于点Q,过点Q作QR⊥BC于点R,连接PR.求△PQR面积的最大值及此时点P的坐标.
(3)如图2,点C关于x轴的对称点为点C′,将抛物线沿射线C′A的方向平移2个单位长度得到新的抛物线y′,新抛物线y′与原抛物线交于点M,原抛物线的对称轴上有一动点N,平面直角坐标系内是否存在一点K,使得以D,M,N,K为顶点的四边形是矩形?若存在,请直接写出点K的坐标;若不存在,请说明理由.
四、解答题:(本大题1个小题,共8分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上
26如图,在正方形ABCD中,E,F分别是边BC,AB上一动点,且AF=BE,连接DF,AE交于点G,连接CG.
(1)如图1,若CG=AD,求证:CE=AD;
(2)如图2,当点E,F分别在边BC,AB上运动时,在以GC为斜边构造等腰直角△CGH,连接DH,猜想∠HDG的大小是否为定值,并证明你的结论;
(3)如图3,在(2)的条件下,连接BH,当BH取得最小值时,请直接写出的值.
答案
一、选择题:(本大题共12个小题,每小题4分,共48分)在每个小题的下面都给出了代号为A、B、C、D的四个答案其中只有一个是正确的,请将答题卡上题号右侧正确答案所对应的方框涂黑
1:D.
2:C.
3:C.
4:C.
5:D.
6:D.
7:C.
8:B.
9:D.
10:B.
11:D.
12:A.
二、填空题:(本大题共6个小题,每小题4分,共24分)请将每小题的答案直接填在答题卡中对应的横线上
13:2.8×10﹣8.
14:3.
15:.
16 .36﹣12﹣4π.
17 ..
18:1.
三、解答题:(本大题共7个小题,每小题10分,共70分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上
19
解:(1)(x﹣y)2﹣y(x﹣2y)
=x2﹣2xy+y2﹣xy+2y2
=x2﹣3xy+3y2;
(2)(a+)÷
=
=
=
=.
20
解:(1)如图,BD为所作;
(2)过D点作DE⊥BC于E,如图,
∵BD平分∠ABC,
∴∠DBC=∠ABC=×60°=30°,
设CE=x,
∵∠C=45°,
∴DE=CE=x,
在Rt△BDE中,BE=DE=x,
∵BC=3+,
∴x+x=3+,解得x=,
∴△BDC的面积=×(3+)×=.
21
解:(1)女生C组所占的百分比为:15÷40=37.5%,
360°×(1﹣37.5%﹣40%﹣20%)=9°,
中位数落在C组,将成绩从小到大排列处在第20、21位的两个数的平均数为=88.5,因此中位数b=88.5;
A组人数为:40×(1﹣37.5%﹣40%﹣20%)=1(人),
B组人数为:40×20%=8(人),
C组人数为:15(人),出现次数最多的是89,共4个,
D组人数为:40×40%=16(人),得100分的有40×25%=10个,
故众数c=100,
故答案为:9,88.5,100;
(2)女生的知识竞赛成绩更好,
理由:∵男生和女生的平均数相等,但女生的中位数和满分率都高于男生,
∴女生的知识竞赛成绩更好;
(3)估计该校2400名学生此次考试中优秀的人数2400×=870(名).
答:估计我校2400名学生此次知识竞赛中优秀的人数是870名.
22
解:(1)设第一周香椿销售单价是每千克x元,第二周香椿销售单价是每千克y元,
依题意得:,
解得:.
答:第二周香椿销售单价是每千克60元.
(2)依题意得:60(1﹣a%)×180×(1+a%)×+60×180×(1+a%)×(1﹣)=60×180×(1+a%),
令m=a%,则原方程可变形为5000m2﹣700m=0,
解得:m1=0.14,m2=0(不合题意,舍去).
又∵m=a%,
∴a=14.
答:a的值为14.
23
解:(1)将x=﹣2代入y=|x﹣|,得y=0,
将x=2代入y=|x﹣|,得y=0,
将x=3代入y=|x﹣|,得y=,
∴a=0,b=0,c=;
(2)函数图象如下图所示:
(3)令y2=x+2,其图象如图2所示,
由图可知不等式组|x﹣|≥x+2的解是:x≤﹣2.8或﹣1.3≤x≤0或0≤x≤1.2或x≥4.
24
(1)∵6342÷6=1057,(6+3+4+2)÷6=2.5.
∴6342不是“三牛数”.
∵6738÷6=1123,(6+7+3+8)÷6=4.
∴6738是“三牛数”.
(2)设n=,即这个四位数的百位,十位,个位数字分别为a,b,c.
∴n′=.
∴n=×100+,n′=×100+.
∴T(n)==(×100+﹣×100﹣)
=﹣.
当﹣最大时,T(n)最大,此时应该使b尽可能小.
①当b=1时,a=2b﹣2=0.
∴n=,此时6+0+1+c=c+7能被6整除,故c=5.
但6015不能被6整除.
②b=2时,a=2b﹣2=2,此时,n=.
6+2+2+c=10+c能被6整除,取c=2,n=6222.
6222÷6=1037.
∴T(n)的最大值=62﹣22=40.
25
解:(1)∵B点在x轴上,且B点在y=x﹣4上,
∴B(8,0),
∵A(﹣2,0),B(8,0),都在抛物线y=ax2+bx﹣4上,
∴x=﹣2,x=8是方程ax2+bx﹣4=0的两个根,
∴﹣16=﹣,=6,
∴a=,b=﹣,
∴y=x2﹣x﹣4;
(2)∵AD∥BC,直线BC的解析式为y=x﹣4,
∴直线AD的解析式为y=x+1,
过点B作BG⊥AD交点G,
∵QR⊥BC,
∴QR=BG,
在Rt△ABG中,AB=10,tan∠BAG=,
∴BG=2,
设P(m,m2﹣m﹣4),R(n,n﹣4),则Q(m,m+1),
∵QR=2,
∴20=(m﹣n)2+,
∴n﹣m=2,
∴R(m+2,m﹣3),
S△PQR=×(m+1﹣m2+m+4)×2=﹣m2+2m+5=﹣(m﹣4)2+9,
∴当m=4时,S△PQR有最大值9,
∴P(4,﹣6);
(3)∵点C关于x轴的对称点为点C′,
∴C'(0,﹣4),
∴直线AC的解析式为y=2x+4,
∵抛物线沿射线C′A的方向平移2个单位长度,
∴抛物线沿着x轴负方向平移2个单位长度,沿着y轴负方向平移4个单位长度,
∵y=x2﹣x﹣4=(x﹣3)2﹣,
∴y'=(x﹣1)2﹣,
联立(x﹣3)2﹣=(x﹣1)2﹣,解得x=6,
∴M(6,﹣4),
联立x+1=x2﹣x﹣4,解得x=10或x=﹣2,
∵D异于点A,
∴D(10,6),
∵y=x2﹣x﹣4的对称轴为直线x=3,
设N(3,t),K(x,y),
①当DM与KN为矩形对角线时,
DM的中点与KN的中点重合,
∴8=,1=,
∴x=13,t=2﹣y,
∵DM=KN,
∴16+100=(3﹣x)2+(t﹣y)2,
∴y=﹣1或y=3,
∴K(13,﹣1)或K(13,3);
②当DN与MK为矩形对角线时,
DN的中点与MK的中点重合,
∴=,=,
∴x=7,t=y﹣10,
∵DN=MK,
∴49+(6﹣t)2=(6﹣x)2+(y+4)2,
∴y=,
∴K(7,);
③当KD与MN为矩形对角线时,
KD的中点与MN的中点重合
∴=,=,
∴x=﹣1,t=10+y,
∵KD=MN,
∴(x﹣10)2+(6﹣y)2=9+(t+4)2,
∴y=﹣,
∴K(﹣1,﹣);
综上所述:以D,M,N,K为顶点的四边形是矩形时,K点坐标为(﹣1,﹣)或(7,)或(13,﹣1)或(13,3).
四、解答题:(本大题1个小题,共8分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上
26
(1)延长DC、AE相交于点K,如图:
∵四边形ABCD是正方形,
∴AD=BA,∠DAF=90°=∠ABE,
∵AF=BE,
∴△ADF≌△BAE(SAS),
∴∠ADF=∠BAE,
∴∠AFG+∠BAE=∠AFG+∠ADF=90°,
∴DF⊥AE,
∴∠K+∠CDG=90°=∠DGK=∠CGD+∠CGK,
∵CG=CD,
∴∠CDG=∠CGD,
∴∠K=∠CGK,
∴CK=CG=CD=AB,
又∠CEK=∠AEB,∠ECK=∠EBA=90°,
∴△CEK≌△BAE(AAS),
∴CE=BE=BC=AD;
(2)∠HDG=45°;证明如下:
连接AC,如图:
∵四边形ABCD是正方形,
∴CA=CD,∠ACD=45°,
∵等腰直角△HGC,
∴CG=CH,∠GCH=45°,
∴==,∠ACG=∠DCH,
∴△ACG∽△DCH,
∴∠CHD=∠CGA=∠CGH+∠AGD+∠DGH=135°+∠DGH,
∴∠DHG=360°﹣∠CHG﹣∠CHD
=360°﹣90°﹣(135°+∠DGH)
=135°﹣∠DGH,
∵∠DHG=180°﹣∠HDG﹣∠DGH,
∴135°﹣∠DGH=180°﹣∠HDG﹣∠DGH,
∴∠HDG=45°;
(3)过点C作CN⊥DF于点N,取CD的中点M,以DM为斜边在正方形外作等腰Rt△DOM,过点O作OT⊥BC,交BC的延长线于点T,过点H作HL⊥BC于点L,过点O作OS⊥CD于点S,连接OH、MN、OB,
∵∠CDN+∠ADG=90°=∠DAG+∠ADG,
∴∠CDN=∠DAG,
∵∠CND=90°=∠DGA,CD=DA,
∴△CDN≌△DAG(AAS),
∴DN=AG,
由(2)可知:∠GDH=45°,AG=DH,
∴DN=DH,∠GDH=45°=∠MDO,
∴∠NDM=∠HDO,
∵DM=DO,
∴==,
∴△DMN∽△DOH,
∴=,
∵MN是Rt△CDN斜边上的中线,
∴DM=MN,
∴OH=DO=DM=CD,
∵TC=OS=DM=CD,
∴OT=CS=CD,BT=CD,
∴OB==CD,
∴BH≥OB﹣OH=CD,
故当BH取得最小值时,B、H、O共线,
此时由HL∥OT,可得:
==,
即:=,
∴=,
∴==•=.
平均数
中位数
众数
满分率
女生
90
b
c
25%
男生
90
88
98
15%
x
…
﹣5
﹣4
﹣3
﹣2
﹣1
1
2
3
4
5
6
…
y
…
3
a
3
3
b
c
3
…












