2019_2020学年深圳市宝安区新华中学八下期末数学模拟试卷

这是一份2019_2020学年深圳市宝安区新华中学八下期末数学模拟试卷，共14页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共12小题；共60分）
1. 下列图形中，绕某个点旋转 180∘ 后．能与自身重合的有
（1）正方形；（2）长方形；（3）等边三角形；（4）线段；（5）角；（6）平行四边形．
A. 5 个B. 4 个C. 3 个D. 2 个

2. 将矩形纸片 ABCD 对折，设折痕为 MN，再把 B 点叠在折痕线 MN 上（如图点 Bʹ），若 AB=3，则折痕 AE 的长为
A. 323B. 343C. 2D. 23

3. 如图，在正方形 ABCD 中，E 为 DC 边上的点，连接 BE，将 △BCE 绕点 C 顺时针方向旋转 90∘ 得到 △DCF，连接 EF，若 ∠BEC=60∘，则 ∠EFD 的度数为
A. 10∘B. 15∘C. 20∘D. 25∘

4. 受今年五月份雷暴雨影响，深圳某路段长 120 米的铁路被水冲垮了，施工队抢分夺秒每小时比原计划多修 5 米，结果提前 4 小时开通了列车．若原计划每小时修 x 米，则所列方程正确的是
A. 120x−120x+5=4B. 120x+5−120x=4C. 120x−5−120x=4D. 120x−120x−5=4

5. 解方程 2x+1+51−x=mx2−1 会产生增根，则 m 等于
A. −10B. −10 或 −3C. −3D. −10 或 −4

6. 若分式 3yx−y 的值为 5，则 x，y 同时 扩大 2 倍后，这个分式的值为
A. 52B. 5C. 10D. 25

7. 如图，平行四边形 ABCD 中，EF 过对角线的交点 O，AB=4，AD=3，OF=1.3，则四边形 BCEF 的周长为
A. 8.3B. 9.6C. 12.6D. 13.6

8. 某种商品的进价为 800 元，出售时标价为 1200 元，后来由于该商品积压，商店准备打折销售，但要保证利润率不低于 5%，则至多可打
A. 6 折B. 7 折C. 8 折D. 9 折

9. 如图，已知直角坐标系中的点 A，B 的坐标分别为 A2,4，B4,0，且 P 为 AB 的中点．若将线段 AB 向右平移 3 个单位后，与点 P 对应的点为 Q，则点 Q 的坐标是
A. 3,2B. 6,2C. 6,4D. 3,5

10. 如图，平行四边形 ABCD 绕点 A 逆时针旋转 30∘，得到平行四边形 ABʹCʹDʹ（点 Bʹ 与点 B 是对应点，点 Cʹ 与点 C 是对应点，点 Dʹ 与点 D 是对应点），点 Bʹ 恰好落在 BC 边上，则 ∠C 等于
A. 100∘B. 105∘C. 115∘D. 120∘

11. 在四边形 ABCD 中，对角线 AC，BD 相交于点 O，在① AB=CD；② AB∥CD；③ OA=OC；④ OB=OD；⑤ AC⊥BD；⑥ AC 平分 ∠BAD 这六个条件，则下列各组组合中，不能推出四边形 ABCD 为菱形的是
A. ①②⑤B. ①②⑥C. ③④⑥D. ①②④

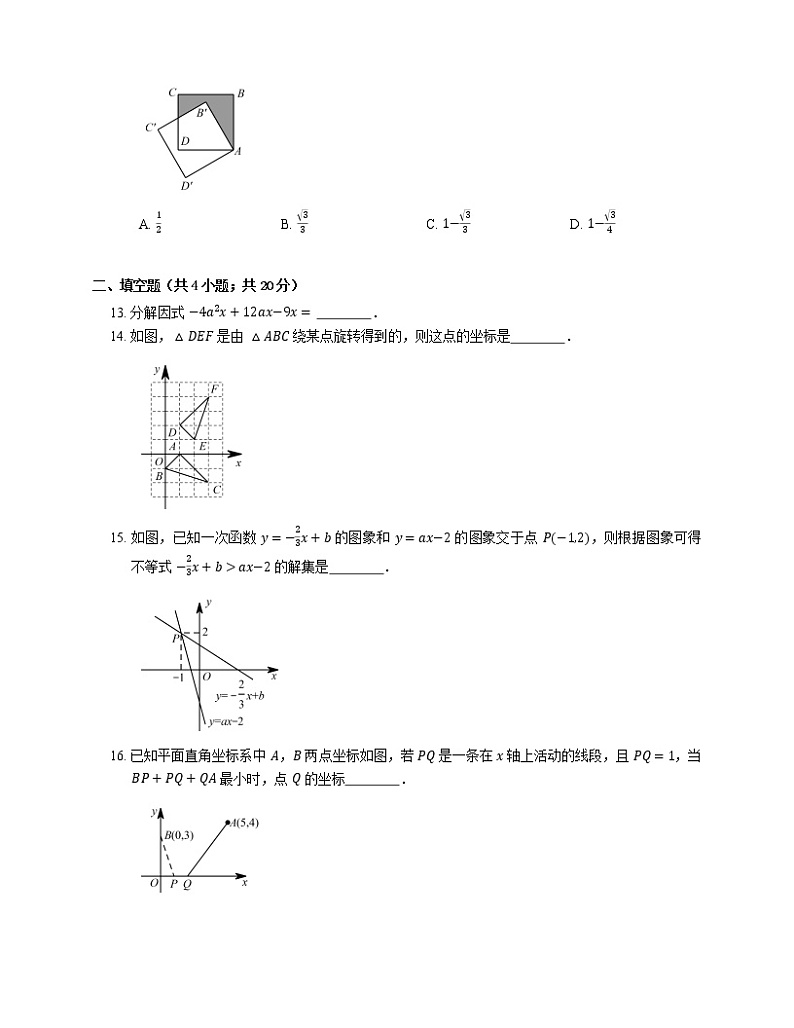
12. 如图，边长为 1 的正方形 ABCD 绕点 A 逆时针旋转 30∘ 到正方形 ABʹCʹDʹ，图中阴影部分的面积为
A. 12B. 33C. 1−33D. 1−34

二、填空题（共4小题；共20分）
13. 分解因式 −4a2x+12ax−9x= ．

14. 如图，△DEF 是由 △ABC 绕某点旋转得到的，则这点的坐标是 ．

15. 如图，已知一次函数 y=−23x+b 的图象和 y=ax−2 的图象交于点 P−1,2，则根据图象可得不等式 −23x+b>ax−2 的解集是 ．

16. 已知平面直角坐标系中 A，B 两点坐标如图，若 PQ 是一条在 x 轴上活动的线段，且 PQ=1，当 BP+PQ+QA 最小时，点 Q 的坐标 ．

三、解答题（共8小题；共104分）
17. 解不等式组 7x−5+2x+1>−15,2x+13−3x−12<0, 并求出其整数解．

18. 先化简，再求值：a2−1a2+6a+9÷a+1×a2−9a−1，其中 a=−2．

19. 解分式方程：3−12−x=x−1x−2．

20. 如图所示，在边长为 1 的网格中作出 △ABC 绕点 A 按逆时针方向旋转 90∘，再向下平移 2 格后的图形 △AʹBʹCʹ．

21. 如图，已知 △ABC，AB=AC，∠A=36∘．
（1）用尺规作线段 AB 的垂直平分线，垂足为 M，交 AC 于 N（不写作法，保留作图痕迹）；
（2）求证：△BNC 是等腰三角形．

22. 如图，在平行四边形 ABCD 中，F 是 AD 的中点，延长 BC 到点 E，使 CE=12BC，连接 DE，CF．
（1）求证：四边形 CEDF 是平行四边形；
（2）若 AB=4，AD=6，∠B=60∘，求 DE 的长．

23. 绿谷商场“家电下乡”指定型号冰箱、彩电的进价和售价如下表所示：
类别冰箱彩电进价元/台23201900售价元/台24201980
（1）按国家政策，农民购买“家电下乡”产品可享受售价 13% 的政府补贴．农民田大伯到该商场购买了冰箱、彩电各一台，可以享受多少元的政府补贴?
（2）为满足农民需求，商场决定用不超过 85000 元采购冰箱、彩电共 40 台，且冰箱的数量不少于彩电数量的 56．
①请你帮助该商场设计相应的进货方案；
②哪种进货方案商场获得利润最大（利润=售价−进价），最大利润是多少?

24. 如图，在平面直角坐标系中，O 是坐标原点，平行四边形的顶点 C 的坐标为 8,8，顶点 A 的坐标为 −6,0，边 AB 在 x 轴上，点 E 为线段 AD 的中点，点 F 在线段 DC 上，且横坐标为 3，直线 EF 与 y 轴交于点 G，有一动点 P 以每秒 1 个单位长度的速度，从点 A 沿折线 A−B−C−F 运动，当点 P 到达点 F 时停止运动，设点 P 运动时间为 t 秒．
（1）求直线 EF 的表达式及点 G 的坐标；
（2）点 P 在运动的过程中，设 △EFP 的面积为 S（P 不与 F 重合），试求 S 与 t 的函数关系式；
（3）在运动的过程中，是否存在点 P，使得 △PGF 为直角三角形?若存在，请直接写出所有符合条件的点 P 的坐标；若不存在，请说明理由．
答案
第一部分
1. B【解析】所有的平行四边形绕对角线的交点旋转 180∘ 后都能与原图形重合，所以（1），（2），（6）正确；
线段绕中点旋转 180∘ 能与原图形重合，（4）正确．
所以绕某个点旋转 180∘ 后，能与自身重合的有（1）正方形，（2）长方形，（4）线段，（6）平行四边形，共有 4 个．
2. C【解析】如图延长 EBʹ 与 AD 交于点 F；
∵∠ABʹE=∠B=90∘，MN 是对折折痕，
∴EBʹ=FBʹ，∠ABʹE=∠ABʹF,
在 △AEBʹ 和 △AFBʹ，
ABʹ=ABʹ,∠ABʹE=∠ABʹF,EBʹ=FBʹ,
∴△AEBʹ≌△AFBʹ，
∴AE=AF，
∴∠BʹAE=∠BʹAD．
故根据题意，易得 ∠BAE=∠BʹAE=∠BʹAD；
故 ∠EAB=30∘，
∴EB=12EA，
设 EB=x，AE=2x，
∴2x2=x2+AB2，得 x=1，
∴AE=2，
则折痕 AE=2．
3. B【解析】因为 △BCE 绕点 C 顺时针方向旋转 90∘ 得到 △DCF，
所以 CE=CF，∠DFC=∠BEC=60∘，∠EFC=45∘，
所以 ∠EFD=60∘−45∘=15∘
4. A【解析】题中原计划修 120x 小时，实际修了 120x+5 小时，
可列得方程 120x−120x+5=4．
5. D
【解析】2x−2−5x−5=m，即 −3x−7=m，由分式方程有增根，得到 x+1x−1=0，即 x=1 或 x=−1，把 x=1 代入整式方程得：m=−10，把 x=−1 代入整式方程得：m=−4．
6. B
7. B
8. B【解析】设打了 x 折.
由题意得，1200×0.1x−800≥800×5%，
解得：x≥7．
答：至多打 7 折．
9. B【解析】根据中点坐标的求法可知点 P 坐标为 3,2，因为左右平移点的纵坐标不变，由题意向右平移 3 个单位，则各点的横坐标加 3，所以点 Q 的坐标是 6,2．
10. B
【解析】∵ 平行四边形 ABCD 绕点 A 逆时针旋转 30∘，得到平行四边形 ABʹCʹDʹ（点 Bʹ 与点 B 是对应点，点 Cʹ 与点 C 是对应点，点 Dʹ 与点 D 是对应点），
∴AB=ABʹ，∠BABʹ=30∘，
∴∠B=∠ABʹB=180∘−30∘÷2=75∘，
∴∠C=180∘−75∘=105∘．
11. D【解析】∵ AB=CD；AB∥CD，
∴ 四边形 ABCD 是平行四边形，
如果加上条件⑤ AC⊥BD 可利用对角线互相垂直的平行四边形是菱形进行判定；
如果加上条件⑥ AC 平分 ∠BAD 可证明邻边相等，根据邻边相等的平行四边形是菱形进行判定；
∵ OA=OC，OB=OD，
∴ 四边形 ABCD 是平行四边形，
如果加上条件⑥ AC 平分 ∠BAD 可证明邻边相等，根据邻边相等的平行四边形是菱形进行判定．
12. C【解析】如图，设 BʹCʹ 与 CD 的交点为 E，连接 AE，
在 Rt△ABʹE 和 Rt△ADE 中，
AE=AE,ABʹ=AD,
∴Rt△ABʹE≌Rt△ADE，
∴∠DAE=∠BʹAE，
∵ 旋转角为 30∘，
∴∠DABʹ=60∘，
∴∠DAE=12×60∘=30∘，
∴DE=1×33=33，
∴ 阴影部分的面积 =1×1−2×12×1×33=1−33．
第二部分
13. −x2a−32
【解析】−4a2x+12ax−9x=−x4a2−12a+9=−x2a−32.
14. 0,1
【解析】如图，连接 AD,BE，作线段 AD,BE 的垂直平分线，
两线的交点即为旋转中心 Oʹ．其坐标是 0,1．
15. x>−1
【解析】∵ 一次函数 y=−23x+b 的图象和 y=ax−2 的图象交于点 P−1,2，
∴ 不等式 −23x+b>ax−2 的解集是 x>−1．
16. 197,0
【解析】如图把点 B 向右平移 1 个单位得到 E1,3，作点 E 关于 x 轴的对称点 F1,−3，连接 AF，AF 与 x 轴的交点即为点 Q，此时 BP+PQ+QA 的值最小．
设直线 AF 的解析式为 y=kx+b，则有 k+b=−3,5k+b=4, 解得 k=74,b=−194,
∴ 直线 AF 的解析式为 y=74x−194，
令 y=0，得到 x=197，
∴ Q197,0．
第三部分
17. 解不等式
7x−5+2x+1>−15.
得：
x>2.
解不等式
2x+13−3x−12<0.
得：
x>1.
则不等式组的解集为 x>2，
∴ 不等式组的整数解为大于 2 的所有整数．
18. 原式=a+1a−1a+32⋅1a+1⋅a+3a−3a−1=a−3a+3.
当 a=−2 时，原式=−5．
19. 分式的两边都乘以 x−2 得：
3x−2+1=x−1,∴3x−6+1=x−1,∴2x=4,
即
x=2,
检验：当 x=2 时，
x−2=0,∴x=2
是原方程的增根，
∴ 原方程无解．
20. 如图所示，红色三角形为 △ABC 绕点 A 按逆时针方向旋转 90∘ 的三角形，△AʹBʹCʹ 即为所要求作的三角形．
21. （1） 如图 1 直线 MN 即为所求．
（2） 连接 BN，如图 2．
∵MN 是 AB 的垂直平分线，
∴NA=NB，
∴∠A=∠NBA=36∘，
∴∠BNC=∠A+∠ABN=72∘，
∵AB=AC，∠A=36∘，
∴∠C=∠ABC=12×180∘−36∘=72∘，
∴∠C=∠CNB，
∴BN=BC，
∴△BNC 是等腰三角形．
22. （1） 在平行四边形 ABCD 中，AD∥BC，AD=BC．
∵ F 是 AD 中点，
∴ DF=12AD．
又 CE=12BC，
∴ DF=CE 且 DF∥CE．
∴ 四边形 CEDF 为平行四边形．
（2） 过点 D 作 DH⊥BE 于点 H，
在平行四边形 ABCD 中，
∵ ∠B=60∘，
∴ ∠DCE=60∘．
∵ AB=4，
∴ CD=4．
∴ CH=2，DH=23．
在平行四边形 CEDF 中，CE=DF=12AD=3．
∴ EH=1．
在 Rt△DHE 中，DE=232+12=13．
23. （1） 2420+1980×13%=572（元），
答：可以享受政府 572 元的补贴；
（2） ①设冰箱采购 x 台，则彩电采购 40−x 台，根据题意得
2320x+190040−x≤85000,x≥5640−x,
解不等式组得 18211≤x≤2137，
因为 x 为正整数，
所以 x=19,20,21．
所以该商场共有 3 种进货方案．
方案一：冰箱购买 19 台，彩电购买 21 台，
方案二：冰箱购买 20 台，彩电购买 20 台，
方案三：冰箱购买 21 台，彩电购买 19 台；
②设商场获得总利润 y 元，根据题意得
y=2420−2320x+1980−190040−x=20x+3200，
因为 20>0，
所以 y 随 x 的增大而增大，
所以当 x=21 时，y最大=20×21+3200=3620 （元），
答：方案三商场获得利润最大，最大利润是 3620 元．
24. （1） 因为 C8,8，DC∥x 轴，点 F 的横坐标为 3，
所以 OD=CD=8．
所以点 F 的坐标为 3,8，
因为 A−6,0，
所以 OA=6，
所以 AD=10，
过点 E 作 EH⊥x 轴于点 H，如图 1，
则 △AHE∽△AOD．
又因为 E 为 AD 的中点，
所以 AHAO=AEAD=EHDO=12．
所以 AH=3，EH=4．
所以 OH=3．
所以点 E 的坐标为 −3,4，
设过 E，F 的直线为 y=kx+b，
所以 3k+b=8,−3k+b=4.
所以 k=23,b=6.
所以直线 EF 为 y=23x+6，
令 x=0，则 y=6，即点 G 的坐标为 0,6．
（2） 延长 HE 交 CD 的延长线于点 M，如图 2，
则 EM=EH=4．
因为 DF=3，
所以 S△DEF=12×3×4=6，
且 S平行四边形ABCD=CD⋅OD=8×8=64．
①当点 P 在 AB 上运动时，如图 3，
S=S平行四边形ABCD−S△DEF−S△APE−S四边形PBCF．
因为 AP=t，EH=4，
所以 S△APE=12×4t=2t，
S四边形PBCF=125+8−t×8=52−4t．
所以 S=64−6−2t−52−4t，即：S=2t+6．
②当点 P 在 BC 边上运动时，如图 4，
S=S平行四边形ABCD−S△DEF−S△PCF−S四边形ABPE．
过点 P 作 PN⊥CD 于点 N．
因为 ∠C=∠A，sin∠A=ODAD=45，
所以 sin∠C=45．
因为 PC=18−t，
所以 PN=PC⋅sin∠C=4518−t．
因为 CF=5，
所以 S△PCF=12×5×4518−t=36−2t．
过点 B 作 BK⊥AD 于点 K．
因为 AB=CD=8，
所以 BK=AB⋅sin∠A=8×45=325．
因为 PB=t−8，
所以 S四边形ABPE=12t−8+5×325=165t−485．
所以 S=64−6−36−2t−165t−485，即 S=−65t+1585．
③当点 P 在 CF 上运动时，如图 5，
因为 PC=t−18，
所以 PF=5−t−18=23−t．
因为 EM=4，
所以 S△PEF=12×4×23−t=46−2t．
综上：S=2t+6,0≤t<8−65t+1585,8≤t<1846−2t,18≤t<23．
（3） 存在．
P15217,2417．
P29117,7617．