2018年广东省佛山市禅城区中考一模数学试卷

这是一份2018年广东省佛山市禅城区中考一模数学试卷，共14页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
1. −3 的倒数是
A. 13B. −13C. 3D. −3

2. 下列汽车标志中，不是轴对称图形的是
A. B.
C. D.

3. 1 cm2 的电子屏上约有细菌 135000 个，135000 用科学记数法表示为
A. 0.135×106B. 1.35×105C. 13.5×104D. 135×103

4. 下列计算正确的是
A. 3+2=6B. x6÷x3=x2C. 4=2D. a2−a2=a4

5. 如图，AB∥CD，∠1=30∘，则 ∠2 的大小是
A. 30∘B. 120∘C. 130∘D. 150∘

6. 下列因式分解正确的是
A. x2+2x−1=x−12B. x2+1=x+12
C. x2−x+1=xx−1+1D. 2x2−2=2x+1x−1

7. 如图，△ABC 内接于 ⊙O，若 ∠A=40∘，则 ∠BCO=
A. 40∘B. 50∘C. 60∘D. 80∘

8. 下列判断错误的是
A. 对角线相等四边形是矩形
B. 对角线相互垂直平分四边形是菱形
C. 对角线相互垂直且相等的平行四边形是正方形
D. 对角线相互平分的四边形是平行四边形

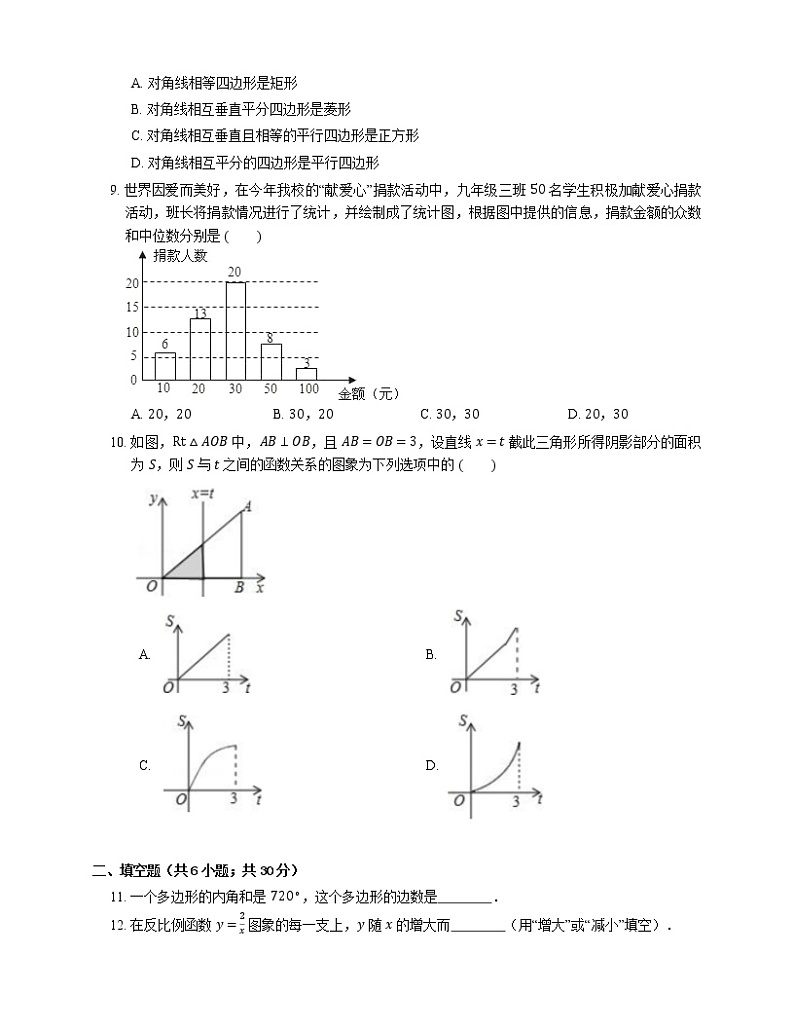
9. 世界因爱而美好，在今年我校的“献爱心”捐款活动中，九年级三班 50 名学生积极加献爱心捐款活动，班长将捐款情况进行了统计，并绘制成了统计图，根据图中提供的信息，捐款金额的众数和中位数分别是
A. 20，20B. 30，20C. 30，30D. 20，30

10. 如图，Rt△AOB 中，AB⊥OB，且 AB=OB=3，设直线 x=t 截此三角形所得阴影部分的面积为 S，则 S 与 t 之间的函数关系的图象为下列选项中的
A. B.
C. D.

二、填空题（共6小题；共30分）
11. 一个多边形的内角和是 720∘，这个多边形的边数是 ．

12. 在反比例函数 y=2x 图象的每一支上，y 随 x 的增大而 （用“增大”或“减小”填空）．

13. △ABC 与 △DEF 是位似图形，且对应面积比为 4:9，则 △ABC 与 △DEF 的位似比为 ．

14. 已知关于 x 的方程 x2−6x+m=0 有两个不相等的实数根，则 m 的取值范围是 ．

15. 如图，在四个小正方体搭成的几何体中，每个小正方体的棱长都是 1，则该几何体的三视图的面积之和是 ．

16. 如图，一根 5 m 长的绳子，一端拴在围墙墙角的柱子上，另一端拴着一只小羊 A（羊只能在草地上活动），那么小羊 A 在草地上的最大活动区域面积是 平方米．

三、解答题（共9小题；共117分）
17. 计算：−12−2−12−3−20+4sin60∘．

18. 先化简再求值：x−3x÷x+9−6xx，其中 x=2+3．

19. 如图，在 △ABC 中，∠C=90∘．
（1）用尺规作图法作 ∠ABC 的平分线 BD，交 AC 于点 D（保留作图痕迹，不要求写作法和证明）；
（2）若 BD=AD=2，求 BC．

20. 已知：如图，在 △ABC 中，AB=AC，AD 是 BC 边的中线，AN 为 △ABC 的外角 ∠CAM 的平分线，CE⊥AN 于点 E，线段 DE 交 AC 于点 F．
（1）求证：四边形 ADCE 为矩形；
（2）线段 DF 与 AB 有怎样的关系?证明你的结论．

21. 某校在开展“校园献爱心”活动中，准备向南部山区学校捐赠男、女两种款式的书包．已知男款书包的单价 50 元/个，女款书包的单价 70 元/个．
（1）原计划募捐 3400 元，购买两种款式的书包共 60 个，那么这两种款式的书包各买多少个?
（2）在捐款活动中，由于学生捐款的积极性高涨，实际共捐款 4800 元，如果购买两种款式的书包共 80 个，那么女款书包最多能买多少个?

22. 某校为了解本校九年级学生足球训练情况，随机抽查该年级若干名学生进行测试，然后把测试结果分为 4 个等级：A，B，C，D，并将统计结果绘制成两幅不完整的统计图．请根据图中的信息解答下列问题．
（1）补全条形统计图；
（2）该年级共有 700 人，估计该年级足球测试成绩为 D 等的人数为 人；
（3）在此次测试中，有甲、乙、丙、丁四个班的学生表现突出，现决定从这四个班中随机选取两个班在全校举行一场足球友谊赛．请用画树状图或列表的方法，求恰好选到甲、乙两个班的概率．

23. 如图，抛物线 y=ax2+bx+2 经过 A−2,0，B−12,0 两点．
（1）求抛物线的函数表达式；
（2）求抛物线的顶点坐标，直接写出当 y<0 时，x 的取值范围；
（3）设点 M 是抛物线的顶点，试判断抛物线上是否存在点 H 满足 ∠AMH=90∘?若存在，请求出点 H 的坐标；若不存在，请说明理由．

24. 在等边 △ABC 中．
（1）如图 1，P，Q 是 BC 边上的两点，AP=AQ，∠BAP=20∘，求 ∠AQB 的度数；
（2）点 P，Q 是 BC 边上的两个动点（不与点 B，C 重合），点 P 在点 Q 的左侧，且 AP=AQ，点 Q 关于直线 AC 的对称点为 M，连接 AM，PM．
①依题意将图 2 补全；
②小茹通过观察、实验提出猜想：在点 P，Q 运动的过程中，始终有 PA=PM，小茹把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：
想法 1：要证明 PA=PM，只需证 △APM 是等边三角形；
想法 2：在 BA 上取一点 N，使得 BN=BP，要证明 PA=PM，只需证 △ANP≌△PCM；
想法 3：将线段 BP 绕点 B 顺时针旋转 60∘，得到线段 BK，要证 PA=PM，只需证 PA=CK，PM=CK⋯
请你参考上面的想法，帮助小茹证明 PA=PM（一种方法即可）．

25. 如图，AB 是 ⊙O 的直径，D 是 BC 的中点，DE⊥AB 于 E，交 CB 于点 F．过点 D 作 BC 的平行线 DM，连接 AC 并延长与 DM 相交于点 G．
（1）求证：GD 是 ⊙O 的切线；
（2）求证：GD2=GC⋅AG；
（3）若 CD=6，AD=8，求 cs∠ABC 的值．
答案
第一部分
1. B【解析】−3 的倒数是 −13．
2. C【解析】A．是轴对称图形，故此选项不合题意；
B．是轴对称图形，故此选项不合题意；
C．不是轴对称图形，故此选项错误；
D．是轴对称图形，故此选项不合题意．
3. B【解析】将 135000 用科学记数法表示为：1.35×105．
4. C【解析】A．原式不能合并，错误；
B．原式=x3，错误；
C．原式=2，正确；
D．原式=−a4，错误．
5. D
【解析】如图，
∵AB∥CD，
∴∠1=∠CEF=30∘，
又 ∵∠2+∠CEF=180∘，
∴∠2=180∘−30∘=150∘．
6. D【解析】A．x2+2x−1，无法直接分解因式，故此选项错误；
B．x2+1，无法直接分解因式，故此选项错误；
C．x2−x+1，无法直接分解因式，故此选项错误；
D．2x2−2=2x+1x−1，正确．
7. B【解析】由圆周角定理得，∠BOC=2∠A=80∘，
∵OB=OC，
∴∠BCO=∠CBO=50∘．
8. A【解析】A．对角线相等四边形是矩形，错误；
B．对角线相互垂直平分四边形是菱形，正确；
C．对角线相互垂直且相等的平行四边形是正方形，正确；
D．对角线相互平分的四边形是平行四边形，正确．
9. C【解析】根据如图提供的信息，捐款金额的众数和中位数分别是 30，30．
10. D
【解析】∵Rt△AOB 中，AB⊥OB，且 AB=OB=3，
∴∠AOB=∠A=45∘，
∵CD⊥OB，
∴CD∥AB，
∴∠OCD=∠A，
∴∠AOD=∠OCD=45∘，
∴OD=CD=t，
∴S△OCD=12×OD×CD=12t20≤t≤3.
即 S=12t20≤t≤3，
故 S 与 t 之间的函数关系的图象应为定义域为 0,3 、开口向上的二次函数图象．
第二部分
11. 6
【解析】∵ 多边形的内角和公式为 n−2⋅180∘，
∴n−2×180∘=720∘，解得 n=6．
∴ 这个多边形的边数是 6．
12. 减小
【解析】∵k=2>0，
∴y 随 x 的增大而减小．
13. 2:3
【解析】△ABC 与 △DEF 是位似图形，且对应面积比为 4:9，
∴△ABC 与 △DEF 的相似比为 2:3．
14. m<9
【解析】∵ 关于 x 的方程 x2−6x+m=0 有两个不相等的实数根，
∴Δ=b2−4ac=−62−4m=36−4m>0，解得：m<9．
15. 9
【解析】主视图是第一层是三个小正方形，第二层右边一个小正方形，主视图的面积是 4，
俯视图是三个小正方形，俯视图的面积是 3，
左视图是下边一个小正方形，第二层一个小正方形，左视图的面积是 2，
几何体的三视图的面积之和是 4+3+2=9．
16. 7712π
【解析】如图．
小羊的活动范围是：S=90π×52360+60π×1360=7712π（平方米）．
第三部分
17. 原式=4−23−1+4×32=3.
18. 原式=x−3x÷x2−6x+9x=x−3x⋅xx−32=1x−3.
当 x=2+3 时，
原式=12=22.
19. （1） 射线 BD 如图所示．
（2） ∵DA=DB=2，
∴∠A=∠ABD，
∵BD 平分 ∠ABC，
∴∠ABD=∠DBC，
∵∠C=90∘，
∴∠A=∠ABD=∠DBC=30∘，
∴BC=BD⋅cs30∘=3．
20. （1） ∵ 在 △ABC 中，AB=AC，AD 是 BC 边的中线，
∴AD⊥BC，∠BAD=∠CAD，
∴∠ADC=90∘，
∵AN 为 △ABC 的外角 ∠CAM 的平分线，
∴∠MAN=∠CAN，
∴∠DAE=90∘，
∵CE⊥AN，
∴∠AEC=90∘，
∴ 四边形 ADCE 为矩形．
（2） DF∥AB，DF=12AB．
理由：
∵ 四边形 ADCE 为矩形，
∴AF=CF，
∵BD=CD，
∴DF 是 △ABC 的中位线，
∴DF∥AB，DF=12AB．
21. （1） 设原计划买男款书包 x 个，则女款书包 60−x 个，
根据题意得：
50x+7060−x=3400.
解得：
x=40.60−x=60−40=20
．
答：原计划买男款书包 40 个，则女款书包 20 个．
（2） 设女款书包能买 y 个，则男款书包 80−y 个，
根据题意得：
70y+5080−y≤4800.
解得：
y≤40.∴
女款书包最多能买 40 个．
22. （1） 总人数为 14÷28%=50 人，B 等人数为 50×40%=20 人．
条形图补充如下：
（2） 56
【解析】该年级足球测试成绩为 D 等的人数为 700×450=56（人）．
（3） 画树状图：
共有 12 种等可能的结果数，其中选取的两个班恰好是甲、乙两个班的情况占 2 种，
∴ 恰好选到甲、乙两个班的概率是 212=16．
23. （1） 将 A−2,0，B−12,0 两点代入抛物线 y=ax2+bx+2 中，可得：4a−2b+2=0,14a−12b+2=0,
解得：a=2,b=5,
所以抛物线的解析式为：y=2x2+5x+2．
（2） −2【解析】抛物线的解析式为：y=2x2+5x+2=2x+542−98．
∴ 抛物线的顶点坐标为 −54,−98，
当 y<0 时，x 的取值范围为：−2 （3） 存在点 H 满足 ∠AMH=90∘，
由（2）知 M 点的坐标为 −54,−98，
如图：作 MH⊥AM 交 x 轴于点 Kx,0，作 MN⊥x 轴于点 N，
∵∠AMN+∠KMN=90∘，∠NKM+∠KMN=90∘，
∴∠AMN=∠NKM，
∵∠ANM=∠MNK，
∴△AMN∽△MKN，
∴ANMN=MNNK，
∴MN2=AN⋅NK，
∴982=2−54x+54，
解得 x=716，
∴K 点坐标为 716,0，
直线 MK 的解析式为 y=23x−724，
∴y=23x−724, ⋯⋯①y=2x2+5x+2. ⋯⋯②
把 ① 代入 ②，化简得 48x2+104x+55=0，
Δ=1042−4×48×55=64×4=256>0，
∴x1=−54，x2=−1112，
将 x2=−1112 代入 y=23x−724，
解得 y=−6572，
∴ 直线 MK 与抛物线有两个交点 M，H，
∴ 抛物线上存在点 H，满足 ∠AMH=90∘，
此时点 H 的坐标为 −1112,−6572．
24. （1） ∵AP=AQ，
∴∠APQ=∠AQP，
∴∠APB=∠AQC，
∵△ABC 是等边三角形，
∴∠B=∠C=60∘，
∴∠BAP=∠CAQ=20∘，
∴∠AQB=∠APQ=∠BAP+∠B=80∘．
（2） 如图 2．
∵AP=AQ，
∴∠APQ=∠AQP，
∴∠APB=∠AQC，
∵△ABC 是等边三角形，
∴∠B=∠C=60∘，
∴∠BAP=∠CAQ，（将线段 BP 绕点 B 顺时针旋转 60∘，得到线段 BK，要证 PA=PM，只需证 PA=CK，PM=CK⋯，请你参考上面的想法，帮助小茹证明 PA=PM）
∵ 点 Q 关于直线 AC 的对称点为 M，
∴AQ=AM，∠QAC=∠MAC，
∴∠MAC=∠BAP，
∴∠BAP+∠PAC=∠MAC+∠CAP=60∘，
∴∠PAM=60∘，
∵AP=AQ，
∴AP=AM，
∴△APM 是等边三角形，
∴AP=PM．证明 △ABP≌△ACM≌△BCK．
25. （1） 连接 OD，如图所示：
∵D 是 BC 的中点，
∴OD⊥BC，OD 平分 BC，
∵AB 是 ⊙O 的直径，
∴∠ACB=90∘，即 AG⊥BC，
∵DM∥BC，
∴DM⊥OD，
∴GD 是 ⊙O 的切线．
（2） ∵GD 是 ⊙O 的切线，AG 是 ⊙O 的割线，
∴GD2=GC⋅AG．
（3） ∵D 是 BC 的中点，
∴BD=CD=6，
∴BN=12BC，AB=AD2+BD2=82+62=10，
∵∠DCH=∠BAH，∠CHD=∠AHB，
∴△CDH∽△ABH，
∴CHAH=DHBH=CDAB=610=35，
∵AB 是 ⊙O 的直径，
∴∠ACB=∠ADB=90∘，
∵DHBH=35，
∴BDBH=45，
∴BH=54BD=54×6=152，
∴DH=35BH=92，
∴AH=AD−DH=8−92=72，
∴CH=35AH=2110，
∴BC=BH+CH=152+2110=485，
∴cs∠ABC=BCAB=48510=2425．