2018年广东省佛山市顺德区中考模拟数学试卷

这是一份2018年广东省佛山市顺德区中考模拟数学试卷，共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
1. sin60∘ 的值为
A. 3B. 32C. 22D. 12

2. 在 △ABC 中，∠C=90∘，AB=10，csA=45，则 BC 的长为
A. 6B. 7.5C. 8D. 12.5

3. 已知 ⊙O 的半径为 3，圆心 O 到直线 L 的距离为 2，则直线 L 与 ⊙O 的位置关系是
A. 相交B. 相切C. 相离D. 不能确定

4. 抛物线 y=x−12+3
A. 有最大值 1B. 有最小值 1C. 有最大值 3D. 有最小值 3

5. 如图，⊙O 是 △ABC 的外接圆，已知 ∠ACO=30∘，则 ∠B 的度数是
A. 30∘B. 45∘C. 60∘D. 75∘

6. 三角形的内心是三角形中
A. 三条高的交点B. 三边垂直平分线的交点
C. 三条中线的交点D. 三条角平分线的交点

7. 正六边形 ABCDEF 内接于 ⊙O，正六边形的周长是 12，则 ⊙O 的半径是
A. 3B. 2C. 22D. 23

8. 二次函数 y=ax2+bx+c 的图象如图所示，则下列结论中错误的是
A. 函数有最小值
B. c<0
C. 当 −10
D. 当 x<12 时，y 随 x 的增大而减小

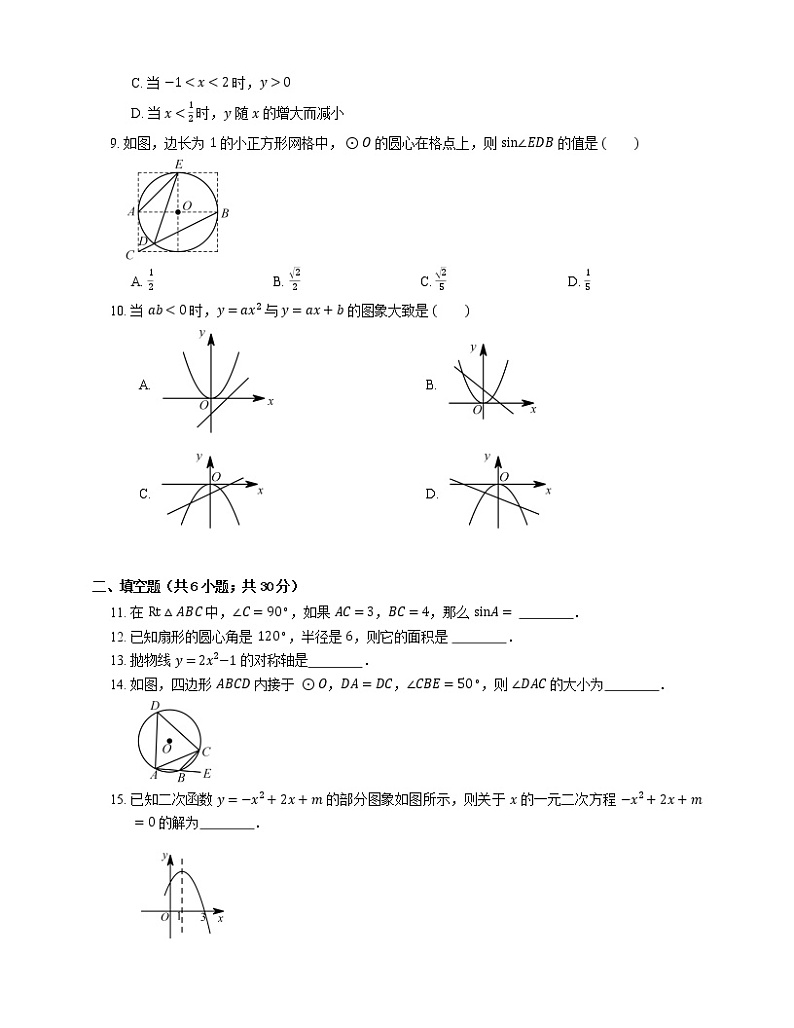
9. 如图，边长为 1 的小正方形网格中，⊙O 的圆心在格点上，则 sin∠EDB 的值是
A. 12B. 22C. 25D. 15

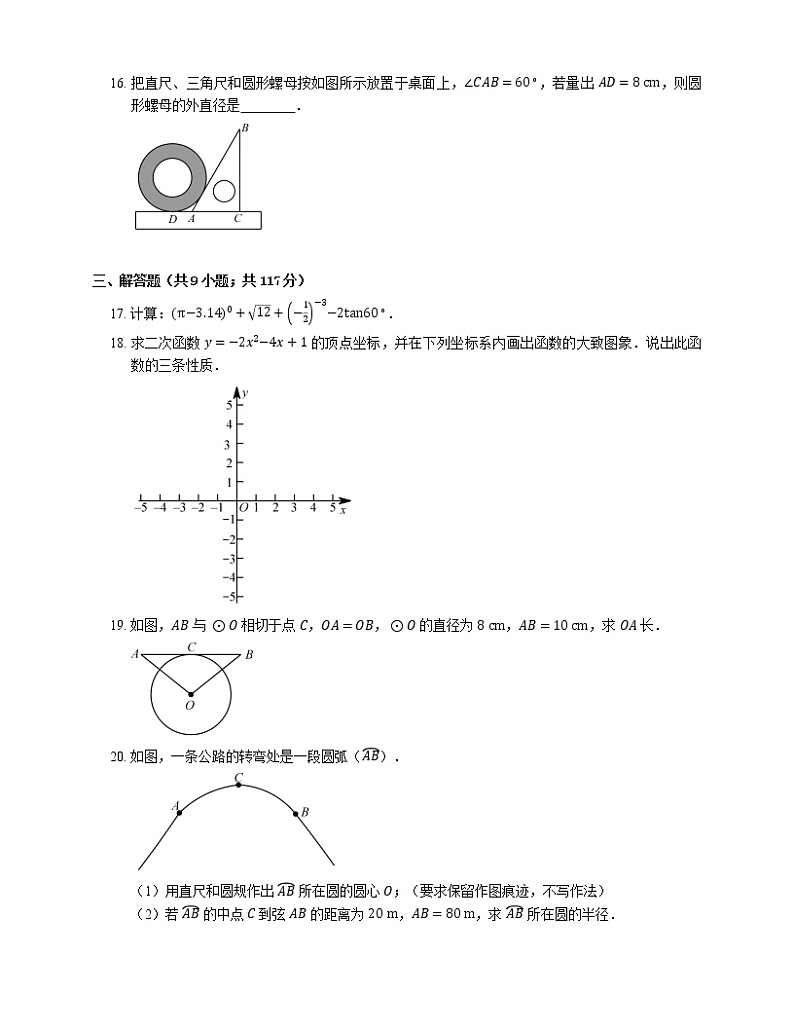
10. 当 ab<0 时，y=ax2 与 y=ax+b 的图象大致是
A. B.
C. D.

二、填空题（共6小题；共30分）
11. 在 Rt△ABC 中，∠C=90∘，如果 AC=3，BC=4，那么 sinA= ．

12. 已知扇形的圆心角是 120∘，半径是 6，则它的面积是 ．

13. 抛物线 y=2x2−1 的对称轴是 ．

14. 如图，四边形 ABCD 内接于 ⊙O，DA=DC，∠CBE=50∘，则 ∠DAC 的大小为 ．

15. 已知二次函数 y=−x2+2x+m 的部分图象如图所示，则关于 x 的一元二次方程 −x2+2x+m=0 的解为 ．

16. 把直尺、三角尺和圆形螺母按如图所示放置于桌面上，∠CAB=60∘，若量出 AD=8 cm，则圆形螺母的外直径是 ．

三、解答题（共9小题；共117分）
17. 计算：π−3.140+12+−12−3−2tan60∘．

18. 求二次函数 y=−2x2−4x+1 的顶点坐标，并在下列坐标系内画出函数的大致图象．说出此函数的三条性质．

19. 如图，AB 与 ⊙O 相切于点 C，OA=OB，⊙O 的直径为 8 cm，AB=10 cm，求 OA 长．

20. 如图，一条公路的转弯处是一段圆弧（AB）．
（1）用直尺和圆规作出 AB 所在圆的圆心 O；（要求保留作图痕迹，不写作法）
（2）若 AB 的中点 C 到弦 AB 的距离为 20 m，AB=80 m，求 AB 所在圆的半径．

21. 一座隧道的截面由抛物线和长方形构成，长方形的长为 8 m，宽为 2 m，隧道最高点 P 位于 AB 的中央且距地面 6 m，建立如图所示的坐标系．
（1）求抛物线的表达式；
（2）一辆货车高 4 m，宽 4 m，能否从该隧道内通过，为什么?

22. 如图，在电线杆上的 C 处引拉线 CE，CF 固定电线杆，拉线 CE 和地面所成的角 ∠CED=60∘，在离电线杆 6 米的 B 处安置测角仪 AB，在 A 处测得电线杆上 C 处的仰角为 30∘，已知测角仪高 AB 为 1.5 米，求拉线 CE 的长（结果精确到 0.1 米，参考数据：2≈1.414，3≈1.732）．

23. 为了美化生活环境，小明的爸爸要在院墙外的一块空地上修建一个矩形花圃．如图所示，矩形花圃的一边利用长 10 米的院墙，另外三条边用篱笆围成，篱笆的总长为 32 米．设 AB 的长为 x 米，矩形花圃的面积为 y 平方米．
（1）用含有 x 的代数式表示 BC 的长，BC= 米；
（2）求 y 与 x 的函数关系式，写出自变量 x 的取值范围；
（3）当 x 为何值时，y 有最大值?

24. 如图，在 Rt△ABC 中，∠A=90∘，O 是 BC 边上一点，以 O 为圆心的半圆与 AB 边相切于点 D，与 AC，BC 边分别交于点 E，F，G，连接 OD，已知 BD=2，AE=3，tan∠BOD=23．
（1）求 ⊙O 的半径 OD；
（2）求证：AE 是 ⊙O 的切线；
（3）求图中两部分阴影面积的和．

25. 如图，抛物线 y=−x2+bx+c 交 x 轴于点 A−3,0 和点 B，交 y 轴于点 C0,3．
（1）求抛物线的函数表达式；
（2）若点 P 在抛物线上，且 S△AOP=4S△BOC，求点 P 的坐标；
（3）如图 b，设点 Q 是线段 AC 上的一动点，作 DQ⊥x 轴，交抛物线于点 D，求线段 DQ 长度的最大值．
答案
第一部分
1. B
2. A
3. A
4. D
5. C
【解析】连接 OA，如图，
∵OA=OC，∠ACO=30∘，
∴∠ACO=∠CAO=30∘，
∴∠AOC=120∘，
∴∠B=60∘．
6. D
7. B【解析】连接 OB，OC，
因为多边形 ABCDEF 是正六边形，
所以 ∠BOC=60∘，
因为 OB=OC，
所以 △OBC 是等边三角形，
所以 OB=BC，
因为正六边形的周长是 12，
所以 BC=2，
所以 ⊙O 的半径是 2．
8. C
9. B
10. A
【解析】根据题意，ab>0，即 a，b 同号，当 a>0 时，b>0，y=ax2 开口向上，过原点，y=ax+b 过一、二、三象限；此时，没有选项符合，
当 a<0 时，b<0，y=ax2 开口向下，过原点，y=ax+b 过二、三、四象限，此时，D选项符合．
第二部分
11. 45
12. 12π
13. y 轴
14. 65∘
15. x1=−1，x2=3
16. 163 cm
第三部分
17. π−3.140+12+−12−3−2tan60∘=1+23−8−23=−7.
18. ∵y=−2x2−4x+1=−2x+12+3，
∴ 抛物线开口向下，对称轴为直线 x=−1，顶点坐标为 −1,3，
在 y=−2x2−4x+1 中，令 y=0 可求得 x=1±62，令 x=0 可得 y=1，
∴ 抛物线与 x 轴的交点坐标为 1+62,0 和 1−62,0，与 y 轴的交点坐标为 0,1，
其图象如图所示，
其性质有：①开口向下，②有最大值 3，③对称轴为直线 x=−1．
19. 连接 OC，
∵AB 与 ⊙O 相切于点 C，
∴OC⊥AB，
∵OA=OB，
∴AC=BC=5，
在 Rt△AOC 中，OA=AC2+OC2=52+42=41cm．
答：OA 的长为 41 cm．
20. （1） 如图，点 O 为所求．
（2） 如图，连接 OA，OC，OC 交 AB 于 D．
∵ C 为 AB 的中点，
∴ OC⊥AB，
∴ AD=BD=12AB=40，
设 ⊙O 的半径为 r，则 OA=r，OD=OD−CD=r−20，
在 Rt△OAD 中，
∵ OA2=OD2+BD2，
∴ r2=r−202+402，解得 r=50，
即 AB 所在圆的半径是 50 m．
21. （1） 设抛物线的解析式为 y=ax−h2+k，
∵ 顶点 4,6，
∴y=ax−42+6，
∵ 它过点 0,2，
∴a0−42+6=2，解得 a=−14，
∴ 设抛物线的解析式为 y=−14x−42+6．
（2） 当 x=2 时，y=5>4，
∴ 该货车能通过隧道．
22. 过点 A 作 AH⊥CD，垂足为 H，
由题意可知四边形 ABDH 为矩形，∠CAH=30∘，
∴AB=DH=1.5，BD=AH=6，
在 Rt△ACH 中，tan∠CAH=CHAH，
∴CH=AH⋅tan∠CAH，
∴CH=6tan30∘=6×33=23，
∵DH=1.5，
∴CD=23+1.5，
在 Rt△CDE 中，
∵∠CED=60∘，sin∠CED=CDCE，
∴CE=CDsin60∘=4+3≈5.7（米）．
答：拉线 CE 的长约为 5.7 米．
23. （1） 32−2x
（2） 由题意可得，
y=x32−2x=−2x2+32x，
因为 32−2x>0,32−2x≤10,
所以 11≤x<16，
即 y 与 x 的函数关系式是 y=−2x2+32x11≤x<16．
（3） 因为 y=−2x2+32x=−2x−82+128，11≤x<16，
所以 x=11 时，y 取得最大值，此时 y=110，
即当 x=11 时，y 取得最大值．
24. （1） ∵AB 与圆 O 相切，
∴OD⊥AB，
在 Rt△BDO 中，BD=2，tan∠BOD=BDOD=23，
∴OD=3．
（2） 连接 OE，
∵AE=OD=3，AE∥OD，
∴ 四边形 AEOD 为平行四边形，
∴AD∥EO，
∵DA⊥AE，
∴OE⊥AC，
∵OE 为圆的半径，
∴AC 为圆 O 的切线；
（3） ∵OD∥AC，
∴BDAB=ODAC，即 22+3=3AC，
∴AC=7.5，
∴EC=AC−AE=7.5−3=4.5，
∴S阴影=S△BDO+S△OEC−S扇形BOD−S扇形EOG=12×2×3+12×3×4.5−90π×32360=3+274−9π4=39−9π4.
25. （1） 把 A−3,0，C0,3 代入 y=−x2+bx+c，
得 0=−9−3b+c,3=c,
解得 b=−2,c=3.
故该抛物线的解析式为：y=−x2−2x+3．
（2） 由（1）知，该抛物线的解析式为 y=−x2−2x+3，则易得 B1,0．
∵S△AOP=4S△BOC，
∴12×3×−x2−2x+3=4×12×1×3．．
整理，得 x+12=0 或 x2+2x−7=0，
解得 x=−1 或 x=−1±22．
则符合条件的点 P 的坐标为：−1,4 或 −1+22,−4 或 −1−22,−4．
（3） 设直线 AC 的解析式为 y=kx+t，将 A−3,0，C0,3 代入，
得 −3k+t=0,t=3,
解得 k=1,t=3.
即直线 AC 的解析式为 y=x+3．
设 Q 点坐标为 x,x+3−3≤x≤0，则 D 点坐标为 x,−x2−2x+3，
QD=−x2−2x+3−x+3=−x2−3x=−x+322+94，
∴ 当 x=−32 时，QD 有最大值 94．