

2020-2021年浙江省杭州市六校九年级上学期数学12月月考试卷及答案
展开
这是一份2020-2021年浙江省杭州市六校九年级上学期数学12月月考试卷及答案,共12页。
九年级上学期数学12月月考试卷
一、选择题〔此题有10小题,每题3分,共30分〕
1.假设 ,那么 = 〔 〕
A. 3:2 B. 2:3 C. 2:1 D. 1:2
2.圆心角为 的弧长为 ,那么扇形的半径为〔 〕
A. 6 B. C. 4 D.
3.函数 的图象与坐标轴的交点个数是〔 〕
A. 0 B. 1 C. 2 D. 3
4.⊙O的半径为5,点 的坐标为〔-1,0〕,点 的坐标为〔-3,4〕,那么点 与⊙O的位置关系是〔 〕
A. 点P在⊙O的外 B. 点P在⊙O的上 C. 点P在⊙O的内 D. 不能确定
5.某校举行以“我为词霸〞为主题的英语单词比赛.决赛阶段只剩下甲,乙,丙,丁四名同学,那么甲.乙同学获得前两名的概率是 〔 〕
A. B. C. D.
6.抛物线 经变换后得到抛物线 ,那么这个变换可以是〔 〕
A. 向左平移2个单位 B. 向右平移2个单位 C. 向左平移5个单位 D. 向右平移5个单位
7.A,B,C在⊙O上,△ABO为正三角形,那么 〔 〕
A. 150° B. 120° C. 150°或 30° D. 120°或 60°
8.如图,假设△ 中, , , 是 的中点, , ,那么点 到边 的距离是 〔 〕
A. 4 B. 6 C. 8 D. 12
9.抛物线 经过 , ,且 ,那么以下不等式中一定成立的是 〔 〕
A. B. C. D.
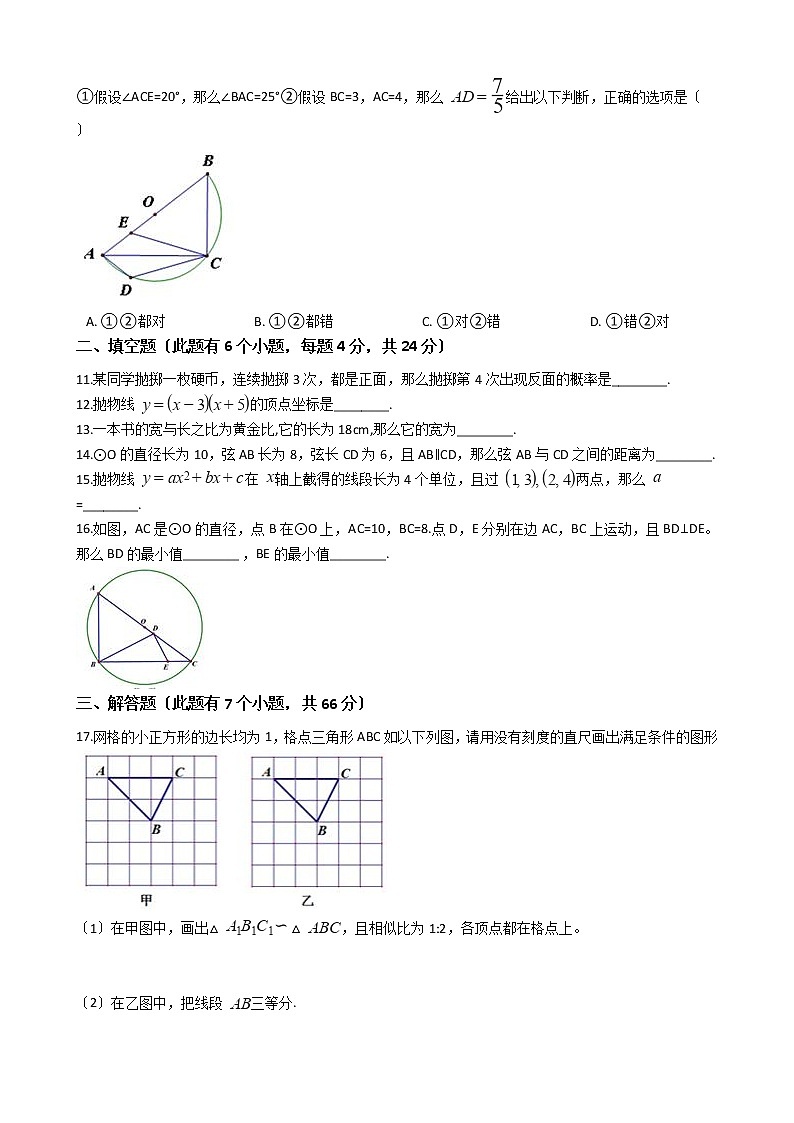
10.如图,在Rt△ABC中,∠ACB=90°,以AB为直径作半圆。点D在弧 上〔不与A,C重合〕,点E在AB上,且点D.E关于AC对称. 给出以下结论:
①假设∠ACE=20°,那么∠BAC=25°②假设BC=3,AC=4,那么 给出以下判断,正确的选项是〔 〕
A. ①②都对 B. ①②都错 C. ①对②错 D. ①错②对
二、填空题〔此题有6个小题,每题4分,共24分〕
11.某同学抛掷一枚硬币,连续抛掷3次,都是正面,那么抛掷第4次出现反面的概率是________.
12.抛物线 的顶点坐标是________.
13.一本书的宽与长之比为黄金比,它的长为18cm,那么它的宽为________.
14.⊙O的直径长为10,弦AB长为8,弦长CD为6,且AB∥CD,那么弦AB与CD之间的距离为________.
15.抛物线 在 轴上截得的线段长为4个单位,且过 两点,那么 =________.
16.如图,AC是⊙O的直径,点B在⊙O上,AC=10,BC=8.点D,E分别在边AC,BC上运动,且BD⊥DE。那么BD的最小值________ ,BE的最小值________.
三、解答题〔此题有7个小题,共66分〕
17.网格的小正方形的边长均为1,格点三角形ABC如以下列图,请用没有刻度的直尺画出满足条件的图形
〔1〕在甲图中,画出△ △ ,且相似比为1:2,各顶点都在格点上。
〔2〕在乙图中,把线段 三等分.
18.四张小卡片上分别写有数字-1,1,2,3,它们除数字外没有任何区别,现将它们放在盒子里搅匀.
〔1〕随机地从盒子里抽取一张,求抽到数字2的概率;
〔2〕随机地从盒子里抽取一张,将数字记为 ,不放回再抽取第二张,将数字记为 ,请你用画树状图或列表的方法表示所有等可能的结果,并求出点 在函数 图象上的概率.
19.如图,在平行四边形ABCD中,EF∥AB.
〔1〕写出所有相似三角形;
〔2〕假设 , ,求 的长.
20.菱形的的两条对角线分别为 与 ,设菱形的面积为 .
〔1〕求y关于x的函数表达式,请写出自变量的取值范围;
〔2〕判断命题“当面积取到最大值时,此菱形为正方形〞是真命题还是假命题?请说明理由.
21.如图,⊙O是△ABC的外接圆,AB=AC,D是优弧BC上的一个动点,连结AD交BC于点E,连结BD.
〔1〕假设AE=2,DE=8,求AC的长;
〔2〕假设D是优弧BC上中点时,求证: .
22.二次函数 的图象经过三点〔1,0〕,〔-3,0〕,〔0, 〕.
〔1〕求该二次函数的解析式;
〔2〕假设反比例函数 图像与二次函数 的图像在第一象限内交于点 , 落在两个相邻的正整数之间,请写出这两个相邻的正整数;
〔3〕假设反比例函数 的图像与二次函数 的图像在第一象限内的交点为A,点A的横坐标为 满足 ,试求实数 的取值范围。
23.如图,在菱形ABCD中, , ,点E是边BC的中点,连接DE,AE.
〔1〕求DE的长;
〔2〕点F为边CD上的一点,连接AF,交DE于点G,连接EF,假设 ,
①求证:△ △ ;
②求DF的长.
答案解析局部
一、选择题〔此题有10小题,每题3分,共30分〕
1.【解析】【解答】解:∵a=2b,∴a∶b=2b∶b=2∶1.
故答案为:C.
【分析】将a=2b代入a∶b就可算出答案.
2.【解析】【解答】解:设该扇形的半径为r,由题意
得 ,
解得 r=.
故答案为:.
【分析】根据弧长的计算公式列出方程,求解即可.
3.【解析】【解答】解:∵ 函数 中a=1>0,
∴图象开口向上,
又∵该函数与y轴交点的坐标为〔0,1〕,
∴ 函数 的图象与坐标轴的交点个数是 1.
故答案为:B.
【分析】根据函数图象的开口方向及与y轴交点坐标即可判断得出答案.
4.【解析】【解答】解:∵ 点 的坐标为〔-1,0〕,点 的坐标为〔-3,4〕 ,
∴OP=,
又∵<5,
∴点P在⊙O的内 .
故答案为:C.
【分析】根据两点间的距离公式算出OP的长,由于OP的长小于该圆的半径,故该点在圆内.
5.【解析】【解答】解:根据题意画出树状图:
由图可知:共有12种等可能的结果数,其中甲、乙恰好是第一名和第二名的结果数为2,
所以甲、乙恰好是第一名和第二名的概率=.
故答案为:D.
【分析】根据题意画出树状图,由图可知:共有12种等可能的结果数,其中甲、乙恰好是第一名和第二名的结果数为2,根据概率公式即可算出答案.
6.【解析】【解答】解:∵ =〔x+1〕2-4,∴其顶点坐标为:〔-1,4〕,
∵ =〔x-1〕2-4,∴其顶点坐标为:〔1,4〕,
∴ 抛物线 向右平移2个单位得到 抛物线 .
故答案为:B.
【分析】首先将各个抛物线的解析式配成顶点式得出其顶点坐标,然后根据点的坐标的平移规律“左减右加〞即可判断得出答案.
7.【解析】【解答】解:∵△ABO为正三角形,∴∠AOB=60°,当点C在优弧上的时候,∠ACB=∠AOB=30°,当点C在劣弧AB上的时候,∠ACB=180°-30°=150°,∴∠ACB的度数为 150°或 30° .
故答案为:C.
【分析】根据等边三角形的性质得出∠AOB的度数,然后分当点C在优弧上的时候与当点C在劣弧AB上的时候两种情况,根据同弧所对的圆周角等于圆心角的一半得出答案.
8.【解析】【解答】解:如图:过点F作FN⊥BC于点点N,过点G作GH⊥BC于点H,过点F作FM⊥AB于点M交FM于点O,
∵ ,
∴∠ADE=∠B=90°,
∵FM⊥AB,∴∠FMB=90°,
∴∠FMB=∠ADE=∠B=90°,
∴DE∥FM∥BC,
∴,
∴DM=BM=6,
∵FN⊥BC,FM⊥AB,
∴∠FNBB=90°,∠FMB=90°,
又∵∠B=90°,
∴四边形FNBM是矩形,
∴FN=BM=6,
∵GH⊥BC,∠B=90°,
∴GH∥BD,
∴,
即,
∴GO=2,
∴GH=GO+OH=8.
故答案为:C.
【分析】首先推出DE∥FM∥BC,根据平行线分线段成比例定理得出, 故DM=BM=6,然后再推出GH∥BD,根据平行线分线段成比例得出, 故GO=2,接着判断出四边形FNBM是矩形,根据矩形的对边相等得出FN=BM=6,最后根据线段的和差即可得出答案.
9.【解析】【解答】解:①a>0时,二次函数图象开口向上,
∵|x1+1|<|x2+1|,
∴y1<y2 ,
∴a(y1−y2)<0,
②a0时与②a
相关试卷
这是一份浙江省杭州市文澜中学2023-2024学年上学期九年级数学12月月考试卷(无答案),共4页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2020-2021年浙江省宁波市九年级上学期数学12月月考试卷及答案,共17页。试卷主要包含了解答题〔共8小题,66分〕等内容,欢迎下载使用。
这是一份2020-2021年浙江省杭州市萧山区九年级上学期数学10月月考试卷及答案,共8页。试卷主要包含了单项选择题,填空题,解答题等内容,欢迎下载使用。









