2020-2021年江苏省东台市九年级上学期数学第二次月考试卷及答案

这是一份2020-2021年江苏省东台市九年级上学期数学第二次月考试卷及答案，共12页。试卷主要包含了单项选择题，填空题，解答题等内容，欢迎下载使用。
 九年级上学期数学第二次月考试卷
一、单项选择题
1.以下方程中，是关于x的一元二次方程的是〔   〕
A. 2x=1﹣x                   B. ax2+bx+c=0                   C. x2﹣2x﹣1                   D. 〔x﹣1〕〔x+2〕=1
2.一组数据﹣1，3，2，0，3，2的中位数是〔   〕
A. 0                                           B. 1                                           C. 2                                           D. 3
3.如果一个多边形的内角和等于1440°，那么这个多边形的边数为〔   〕
A. 8                                          B. 9                                          C. 10                                          D. 11
4.九一(1)班在参加学校4×100 m接力赛时，安排了甲，乙，丙，丁四位选手，他们的顺序由抽签随机决定，那么甲跑第一棒的概率为(   )
A. 1                                          B.                                           C.                                           D. 
5.以下说法中正确的选项是〔  〕

A. 两个平行四边形一定相似                                    B. 两个菱形一定相似
C. 两个矩形一定相似                                              D. 两个等腰直角三角形一定相似
6.设A ，B ，C 是抛物线 上的三点，那么 ， ， 的大小关系为〔 〕
A.                      B.                      C.                      D. 
7.如图，∠MON=90°，△ABC中，AC=BC=13，AB=10，△ABC的顶点A、B分别在边OM、ON上，当点B在边ON上运动时，A随之在OM上运动，△ABC的形状始终保持不变，在运动的过程中，点C到点O的最小距离为〔   〕

A. 5                                         B. 7                                         C. 12                                         D. 
8.小华从二次函数y=ax2+bx+c的图象〔如图〕中观察得到了下面五条信息：
①abc＞0  ②2a﹣3b=0  ③b2﹣4ac＞0  ④a+b+c＞0  ⑤4b＜c
那么其中结论正确的个数是〔   〕

A. 2个                                       B. 3个                                       C. 4个                                       D. 5个
二、填空题
9.函数 自变量 的取值范围是________．

10.一组数据：3，5，x，7，9的平均数为6，那么x=________．
11.如图，AB是⊙O的直径，C是⊙O上的点，过点C作⊙O的切线交AB的延长线于点D．假设∠A=32°，那么∠D=________度．

12.AB∥CD，AD与BC相交于点O.假设 ＝ ，AD＝10，那么AO＝________.

13.如图，正方形ABCD的周长为28cm，那么矩形MNGC的周长是________.

14.假设直角三角形两边分别为6和8，那么它内切圆的半径为________．
15.把抛物线y=﹣x2向上平移2个单位，那么所得抛物线与x轴的两个交点之间的距离是________．
如以下列图的正方形方格纸中，每个小的四边形都是相同的正方形，A、B、C、D都是格点，AB与CD相交于M，那么AM：BM=________．

三、解答题
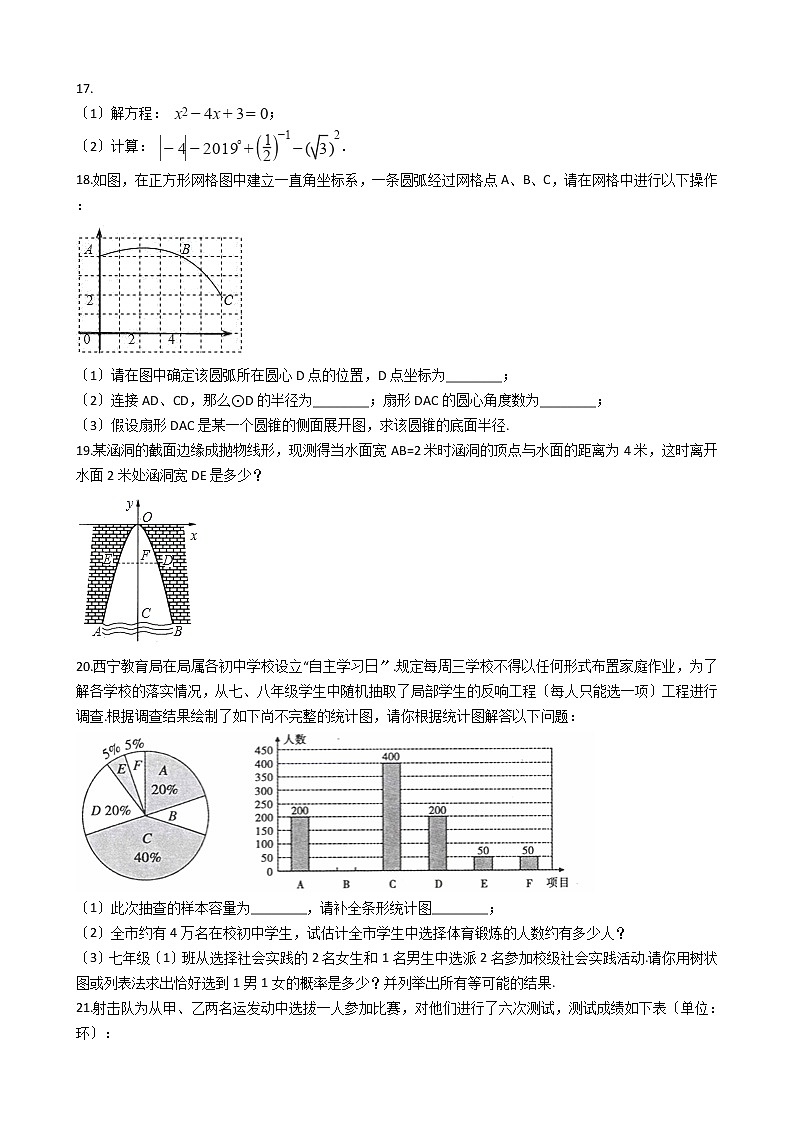
17.    
〔1〕解方程： ；
〔2〕计算： ．
18.如图，在正方形网格图中建立一直角坐标系，一条圆弧经过网格点A、B、C，请在网格中进行以下操作：

〔1〕请在图中确定该圆弧所在圆心D点的位置，D点坐标为________；
〔2〕连接AD、CD，那么⊙D的半径为________；扇形DAC的圆心角度数为________；
〔3〕假设扇形DAC是某一个圆锥的侧面展开图，求该圆锥的底面半径.
19.某涵洞的截面边缘成抛物线形，现测得当水面宽AB=2米时涵洞的顶点与水面的距离为4米，这时离开水面2米处涵洞宽DE是多少？

20.西宁教育局在局属各初中学校设立“自主学习日〞.规定每周三学校不得以任何形式布置家庭作业，为了解各学校的落实情况，从七、八年级学生中随机抽取了局部学生的反响工程〔每人只能选一项〕工程进行调查.根据调查结果绘制了如下尚不完整的统计图，请你根据统计图解答以下问题：

〔1〕此次抽查的样本容量为________，请补全条形统计图________；
〔2〕全市约有4万名在校初中学生，试估计全市学生中选择体育锻炼的人数约有多少人？
〔3〕七年级〔1〕班从选择社会实践的2名女生和1名男生中选派2名参加校级社会实践活动.请你用树状图或列表法求出恰好选到1男1女的概率是多少？并列举出所有等可能的结果.
21.射击队为从甲、乙两名运发动中选拔一人参加比赛，对他们进行了六次测试，测试成绩如下表〔单位：环〕：

〔1〕完成表中填空①________；②________；
〔2〕请计算甲六次测试成绩的方差；
〔3〕假设乙六次测试成绩方差为 ，你认为推荐谁参加比赛更适宜，请说明理由．
22.如图，抛物线 的对称轴为直线 ，且经 、 两点．

〔1〕求抛物线的解析式；
〔2〕在抛物线的对称轴 上，是否存在点 ，使它到点 的距离与到点 的距离之和最小，如果存在求出点 的坐标，如果不存在请说明理由．
23.如图，在等腰三角形ABC中，∠BAC=120°，AB=AC=2，点D是BC边上的一个动点〔不与B、C重合〕，在AC上取一点E，使∠ADE=30°．

〔1〕求证：△ABD∽△DCE；
〔2〕设BD=x，AE=y，求y关于x的函数关系式并写出自变量x的取值范围．
24.如图，AB是⊙O的直径，点C、D在⊙O上，点E在⊙O外，∠EAC=∠D=60°．

〔1〕求∠ABC的度数；
〔2〕求证：AE是⊙O的切线；
〔3〕当BC=4时，求劣弧AC的长．
25.如图，二次函数 的图象与坐标轴交于点A〔-1，0〕和点B〔0，-5〕．

〔1〕求该二次函数的解析式；
〔2〕该函数图象的对称轴上存在一点P，使得△ABP的周长最小，请求出点P的坐标；
〔3〕设二次函数 的图象与x轴的另一交点为点C，连接BC，点N是线段BC上一点，过点N作y轴的平行线交抛物线于点M，求当四边形OBMN为平行四边形时，点N的坐标．
本钱为 元 的水产品，假设按 元 销售，一个月可售出 ，售价毎涨 元，月销售量就减少 ．
〔1〕写出月销售利润 〔元〕与售价 〔元 〕之间的函数表达式；
〔2〕当售价定为多少元时，该商店月销售利润为 元？
〔3〕当售价定为多少元时会获得最大利润？求出最大利润．
27.如图，在Rt△ABC中，∠ACB=90°，AC=8，BC=6，CD⊥AB于点D．点P从点D 出发，沿线段DC向点C运动，点Q从点C出发，沿线段CA向点A运动，两点同时出发，速度都为每秒1个单位长度，当点P运动到C时，两点都停止．设运动时间为t秒．

〔1〕求线段CD的长；
〔2〕当t为何值时，△CPQ是直角三角形？
〔3〕是否存在某一时刻，使得PQ分△ACD的面积为1：11？假设存在，求出t的值，假设不存在，请说明理由．

答案解析局部
一、单项选择题
1.【解析】【解答】解：A． 2x=1﹣x 是一元一次方程；
B． ax2+bx+c=0 ，当a=0时，不是一元二次方程；
C． x2﹣2x﹣1，不是方程；
D．〔x﹣1〕〔x+2〕=1，是一元二次方程．
故答案为：D．

【分析】只含一个未知数，且未知数的最高次数是二次，这样的整式方程叫一元二次方程〔注意：二次项的系数不能为0〕.据此作出判断即可.
2.【解析】【解答】解：将数据重新排列为﹣1、0、2、2、3、3，那么这组数据的中位数为〔2+2〕÷2=2，故答案为：C．
【分析】把一组数据从小到大排列，处在最中间的一个或两个数的平均数叫这组数据的中位数，据此作出判断即可.
3.【解析】【解答】根据题意，得〔n﹣2〕•180＝1440，
解得：n＝10.
所以此多边形的边数为10，
故答案为：C.
【分析】n边形的内角和是〔n﹣2〕•180°，代入就得到一个关于n的方程，就可以解得边数n.
4.【解析】【解答】解：甲跑第一棒的概率为 ．故答案为：D．
【分析】甲抽签有4种可能结果．其中第一棒只有1种，根据概率公式计算即可.
5.【解析】【分析】根据相似图形的形状必须完全相同；相似图形的大小不一定相同进行分析即可．

【解答】A、两个平行四边形一定相似，说法错误；
B、两个菱形一定相似，说法错误；
C、两个矩形一定相似，说法错误；
D、两个等腰直角三角形一定相似，说法正确；
应选：D．
【点评】此题主要考查了相似图形，关键是掌握相似图形定义：把形状相同的图形称为相似形．
6.【解析】【解答】∵函数的解析式是 ，如图，

∴对称轴是 ，
∴点A关于对称轴的点A′是 ，
那么点A′、B、C都在对称轴的右边，而对称轴右边 随 的增大而减小，
∴于是 ，
故答案为：A.

【分析】由题意知，A、B、C三点不在抛物线对称轴的同一侧，根据抛物线的对称性找出点A的对称点A′，再利用二次函数的增减性即可作出判断.
7.【解析】【解答】如以以下列图，取AB的中点D,连接OD，OC,CD，那么OD=5=AD, 因为AC=BC=13，根据勾股定理得，CD=12，当C,O,D三点共线时，OC最小，为12-5=7.故答案为：B.


【分析】取AB的中点D,连接OD，OC，CD，由直角三角形斜边的中线等于斜边的一半可得OD=5，根据三角形的两边之和大于第三边可知，当C,O,D三点共线时，OC最小，根据等腰三角形的性质及勾股定理求出CD，即可可求出点C到点O的最小距离 .
8.【解析】【解答】①因为函数图象与y轴的交点在y轴的负半轴可知，c＜0，
由函数图象开口向上可知，a＞0，由①知，c＜0，
由函数的对称轴在x的正半轴上可知，x＝− ＞0，故b＜0，故abc＞0；故此选项正确；
②因为函数的对称轴为x＝− ＝ ，故2a＝−3b，即2a＋3b＝0；故此选项错误；
③因为图象和x轴有两个交点，所以b2−4ac＞0，故此选项正确；
④把x＝1代入y＝ax2＋bx＋c得：a＋b＋c＜0，故此选项错误；
⑤当x＝2时，y＝4a＋2b＋c＝2×〔−3b〕＋2b＋c＝c−4b，
而点〔2，c−4b〕在第一象限，
∴⑤c−4b＞0，故此选项正确；
其中正确信息的有①③⑤，
故答案为：B．
【分析】由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．
二、填空题
9.【解析】【解答】解：由题意得,
x-5≥0,
∴x≥5.
故答案为：x≥5.
【分析】根据二次根式被开方数为非负数得到 自变量 x 的取值范围
10.【解析】【解答】解：由题意知，〔3+5+x+7+9〕÷5=6，
解得：x=6．
故答案为6．
【分析】根据算术平均数的定义列式计算即可得解．
11.【解析】【解答】连接OC，

由圆周角定理得，∠COD=2∠A=64°，
∵CD为⊙O的切线，
∴OC⊥CD，
∴∠D=90°-∠COD=26°，
故答案为：26．
【分析】连接OC，根据圆周角定理得到∠COD=2∠A，根据切线的性质计算即可．
12.【解析】【解答】∵AB∥CD，
 
解得，AO=4，
故答案是：4．

【分析】根据平行线分线段成比例定理可得AO:OD=BO:OC=2:3，再由AD=10即可求出答案.
13.【解析】【解答】解：∵ABCD为正方形，MN⊥CD，NG⊥BC，∴△DMN和△BNG为等腰直角三角形，
∴MN=DM，NG=BG，∴ =MN+MC+CG+BG=DM+MC+GC+BG=DC+BC=14cm.

【分析】由题意易得△DMN和△BNG为等腰直角三角形，由等腰直角三角形的性质得MN=DM，NG=BG，那么根据矩形MNGC的周长=MN+MC+CG+BG=DM+MC+GC+BG=DC+BC可求解。
14.【解析】【解答】假设8是直角边，那么该三角形的斜边的长为： ，
∴内切圆的半径为： ；
假设8是斜边，那么该三角形的另一条直角边的长为： ，
∴内切圆的半径为： .
故答案为2或 -1.
【分析】根据题意，求第三边的长必须分类讨论，即8是斜边或直角边的两种情况，然后利用勾股定理求出另一边的长，再根据内切圆半径公式求解即可.
15.【解析】【解答】解：所得抛物线为y=﹣x2+2，当y=0时，﹣x2+2=0，解得x=± ，
∴两个交点之间的距离是|﹣ ﹣ |= ．
【分析】先由平移规律求出新抛物线的解析式，然后求出抛物线与x轴的两个交点横坐标，利用坐标轴上两点间距离公式即可求得距离．
16.【解析】【解答】解：作AE∥BC交DC于点E，交DF于点F，

设每个小正方形的边长为a，
那么△DEF∽△DCN，
∴ ＝ ＝ ，
∴EF= a，
∵AF=2a，
∴AE= a，
∵△AME∽△BMC，
∴ ＝ ＝ ＝ ，
故答案为：5：12．
【分析】根据题意作出适宜的辅助线，然后根据三角形相似即可解答此题．
三、解答题
17.【解析】【分析】〔1〕根据因式分解法即可求解一元二次方程；〔2〕根据实数的性质即可化简求解.
18.【解析】【解答】解：〔1〕如图，分别作AB、BC的垂直平分线，两线交于点D，

∴D点的坐标为(2，0).
〔 2 〕连接DA、DC，如图，

那么AD= ，
即⊙D的半径为 .
∵OD=CE，OA=DE=4，
∠AOD=∠CEO=90°，
∴△AOD≌△DEC，
∴∠OAD=∠CDE，
∴∠ADO+∠CDE=∠ADO+∠OAD=90°，
∴∠ADC=90°，
即扇形DAC的圆心角度数为90°.
【分析】〔1〕作AB、BC的垂直平分线，两垂直平分线的交代即为点D，再根据坐标轴上点的坐标特征可得到点D的坐标；〔2〕连接DA、DC，利用勾股定理求出AD的长，即⊙D的半径；再利用SAS证得△AOD≌△DEC，根据全等三角形的性质可得∠OAD=∠CDE，然后求出∠ADC的度数即可；〔3〕设出圆锥的底面半径，再根据圆锥的底面周长等于侧面展开图即扇形的弧长，即可求出该圆锥的底面半径.
19.【解析】【分析】根据点B的坐标利用待定系数法求得函数解析式，再求出离开水面2米处即y=﹣2时x的值，从而得出答案．
20.【解析】【解答】〔1〕总人数=200÷20%=1000，故答案为1000，
B组人数=1000﹣200﹣400﹣200﹣50﹣50=100人，
条形图如以下列图：

【分析】〔1〕根据 =百分比，计算即可；〔2〕用样本估计总体的思想，即可解决问题；〔3〕画出树状图，得到所有可能，以及一男一女的可能数，根据概率公式计算即可；
21.【解析】【解答】〔1〕甲的中位数是： (9+9)=9；乙的平均数是：(10+7+10+10+9+8)÷6=9；
故答案为：9，9；
【分析】〔1〕根据中位数的定义先把这组数据从小到大排列，再找出最中间两个数的平均数即可求出①；根据平均数的计算公式即可求出②；〔2〕根据方差的计算公式S2= [〔x1- 〕2+〔x2- 〕2+…+〔xn- 〕2]代值计算即可；〔3〕根据方差的意义：反映了一组数据的波动大小，方差越大，波动性越大，反之也成立，即可得出答案．
22.【解析】【分析】〔1〕利用待定系数法即可求得函数的解析式；〔2〕抛物线与x轴的除A外的另一个交点C就是A的对称点，那么BC与对称轴的交点就是M，首先求得C的坐标，然后求得BC的解析式，进而求得M的坐标．
23.【解析】【分析】〔1〕根据两角相等得到△ABD∽△DCE；〔2〕如图1，作高AF，根据直角三角形30°的性质求AF的长，根据勾股定理求BF的长，那么可得BC的长，根据〔1〕中的相似列比例式可得函数关系式，并确定取值．
24.【解析】【分析】〔1〕由圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，即可求得∠ABC的度数；〔2〕由AB是⊙O的直径，根据半圆〔或直径〕所对的圆周角是直角，即可得∠ACB=90°，又由∠BAC=30°，易求得∠BAE=90°，那么可得AE是⊙O的切线；〔3〕首先连接OC，易得△OBC是等边三角形，那么可得∠AOC=120°，由弧长公式，即可求得劣弧AC的长．
25.【解析】【分析】〔1〕将A、B的坐标代入抛物线的解析式中，即可求得待定系数的值；〔2〕设抛物线与x轴的另一交点为C，根据〔1〕所得的函数解析式即可求得A、B、C的坐标；在△ABP中，AB的长为定值，假设三角形的周长最小，那么AP＋BP的长最小；由于A、C关于抛物线的对称轴对称，假设连接BC，那么BC与对称轴的交点即为所求的P点，可先求出直线BC的解析式，然后联立抛物线的对称轴方程，即可求得P点的坐标；〔3〕根据OBMN为平行四边形，得到OB=NM=5且OB∥NM,设点N坐标为〔x,x-5〕，那么M点坐标为〔x, 〕得到NM=〔x-5〕-( ),令NM=5即可解出x,即可求解.
26.【解析】【分析】〔1〕根据月销售利润=每千克的利润×数量就可以表示出月销售利润y〔单位：元〕与售价x〔单位：元/千克〕之间的函数解析式；〔2〕当y=8000时，代入〔1〕的解析式求出结论即可，〔3〕将〔1〕的解析式化为顶点式就可以求出结论．
27.【解析】【分析】〔1〕先利用勾股定理求出AB＝10，进利用面积法求出CD；〔2〕先表示出CP，再判断出∠ACD＝∠B，进而分两种情况，利用相似三角形得出比例式建立方程求解，即可得出结论；〔3〕先判断出△CEQ∽△CDA，得出 ，进而表示出QE＝ t，再分当S△CPQ＝ S△ACD时，和当S△CPD＝ S△ACD时，利用面积建立方程求解即可得出结论．