2020-2021年浙江省嘉兴市八年级上学期数学第一次月考试卷

这是一份2020-2021年浙江省嘉兴市八年级上学期数学第一次月考试卷，共12页。

 八年级上学期数学第一次月考试卷
一、选择题〔此题有10小题，每题3分，共30分〕
1.在一些美术字中，有的汉字是轴对称图形．下面4个汉字中，可以看作是轴对称图形的是〔    〕
A.                          B.                          C.                          D. 
2.三角形的三边长分别为2，x，3，那么x可以是〔   〕
A. 1                                           B. 4                                           C. 5                                           D. 6
3.以下命题中，属于假命题的是〔   〕
A. 三角形三个内角的和等于180°                            B. 两直线平行，同位角相等
C. 全等三角形的对应边相等                                    D. 相等的两个角是对顶角
4.如图，△ABC≌△DEF，假设AB=DE，∠B=∠E，那么以下结论错误的选项是〔   〕

A. AC=DF                         B. ∠ACB=∠DFE                         C. BC=EF                         D. ∠BAC=∠EDF
以以下列图中，正确画出AC边上高的是(    )
A.                                             B. 
C.                                          D. 
6.等腰三角形的一个角为72°，那么其顶角为〔   〕
A. 36°                                 B. 72°                                 C. 72°或36°                                 D. 无法确定
7.如图，在△ABC中，AB=AC，AB=5，BC=3，以A，B两点为圆心，大于 AB的长为半径画弧，两弧相交于点M，N，连接MN与AC相交于点D，那么△BDC的周长为(    )

A. 8                                         B. 10                                         C. 11                                         D. 13
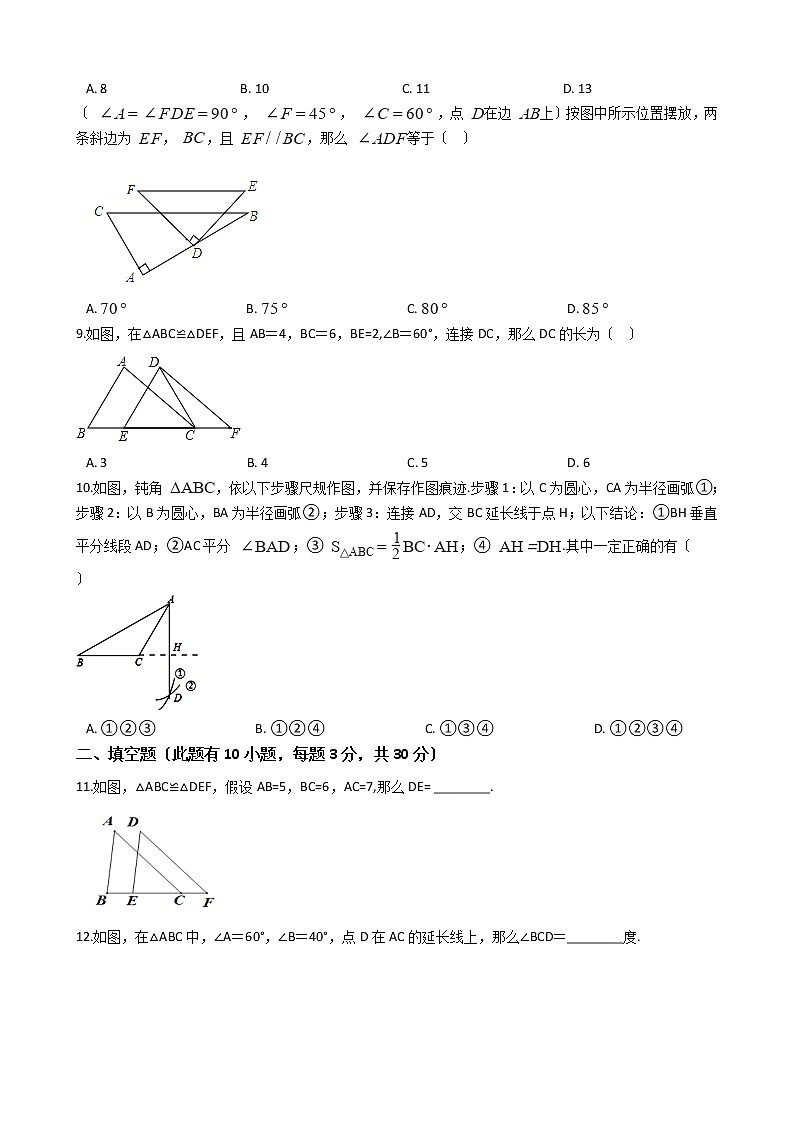
〔 ， ， ，点 在边 上〕按图中所示位置摆放，两条斜边为 ， ，且 ，那么 等于〔   〕

A.                                     B.                                     C.                                     D. 
9.如图，在△ABC≌△DEF，且AB＝4，BC＝6，BE=2,∠B＝60°，连接DC，那么DC的长为〔   〕 

A. 3                                           B. 4                                           C. 5                                           D. 6
10.如图，钝角 ，依以下步骤尺规作图，并保存作图痕迹.步骤1：以C为圆心，CA为半径画弧①；步骤2：以B为圆心，BA为半径画弧②；步骤3：连接AD，交BC延长线于点H；以下结论：①BH垂直平分线段AD；②AC平分 ；③ ；④ .其中一定正确的有〔   〕

A. ①②③                               B. ①②④                               C. ①③④                               D. ①②③④
二、填空题〔此题有10小题，每题3分，共30分〕
11.如图，△ABC≌△DEF，假设AB=5，BC=6，AC=7,那么DE= ________.

12.如图，在△ABC中，∠A＝60°，∠B＝40°，点D在AC的延长线上，那么∠BCD＝________度.

13.三角形的三边长都是整数，其中两边分别为5和1，那么这个三角形的第三边长为________.
14.如图，在等腰三角形ABC中，AB＝AC，DE垂直平分AB.∠ADE＝40°，那么∠DBC＝________度.

15.如图，AC＝BD，要使△ABC≌△DCB，只需增加的一个条件是________.

16.如图，在△ABC中，∠B、∠C的平分线交于O点，过O点作EF∥BC交AB、AC于点E、F.当EF=6，BE=2时，CF的长为________.

17.如图，CD是△ABC的中线，△ABC的面积为100cm2 ， 那么△ACD的面积为________cm2

18.如图，在△ABC中，∠A＝60°，假设剪去∠A得到四边形BCDE，那么∠1+∠2＝________度.

如以下列图的4×4正方形网格中，∠1＋∠2＋∠3＋∠4＋∠5＋∠6＋∠7＝________度.

20.如图，在△ABC中，AB＝AC，∠A＝108°，BD平分∠ABC交AC于点D.

〔1〕填空∠DBC=________度；
〔2〕写出BC、AB、CD三者数量关系________；
三、解答题〔此题有6小题；共40分〕
21.亲爱的同学们：请用没有刻度的直尺和圆规分别作出△ABC的角平分线AD和线段AB的中垂线MN.〔保存作图痕迹,不要求写出作法〕

22.：如图，AC＝AE，∠1＝∠2，AB＝AD.求证：△ABC≌△ADE.

23.： 如图，点B，F，E，C在同一直线上， ， ， .

求证：
〔1〕AF = DE；
〔2〕
24.如图，在△ABC中，AD是△ABC的高线，AE是△ABC的角平分线.∠BAC=80°，∠C=40°.求∠DAE的大小.

25.如图，点D，E分别在等边△ABC的两边AB，AC上，且AD=BE，线段BD，CE交于点P.

〔1〕判断线段BD，CE的数量关系，并证明你的判断；
〔2〕求∠DPC的度数.
26.如图，△ABC中，∠B=∠C，AB=8厘米，BC=6厘米，点D为AB的中点.如果点P在线段BC上以每秒2厘米的速度由B点向C点运动，同时，点Q在线段CA上以每秒a厘米的速度由C点向A点运动，设运动时间为t〔秒〕〔0≤t≤3〕.

〔1〕用含t的代数式表示PC的长度；
〔2〕假设点P、Q的运动速度相等，经过1秒后，△BPD与△CQP是否全等，请说明理由；
〔3〕假设点P、Q的运动速度不相等，当点Q的运动速度a为多少时，能够使△BPD与△CQP全等？

答案解析局部
一、选择题〔此题有10小题，每题3分，共30分〕
1.【解析】【解答】解：A、不是轴对称图形；
B、不是轴对称图形；
C、是轴对称图形；
D、不是轴对称图形；
故答案为：C．
【分析】根据轴对称图形的概念求解．
2.【解析】【解答】解：∵3-2 ∴1 故答案为：B.

【分析】根据三角形两边之和大于第三边，两边之差小于第三边，列不等式求出x的范围，即可得出结果.
3.【解析】【解答】解：A、 “三角形三个内角的和等于180° 〞是真命题；
B、“两直线平行，同位角相等〞是真命题；
C、“全等三角形的对应边相等〞是真命题；
D、 两直线平行，同位角相等，但同位角不是对顶角，故是假命题；
故答案为：D.

【分析】根据三角形的内角和定理对A作判断，根据平行线的性质定理对B作判断，根据全等三角形的性质对C进行判断，举一反例对D作否认.
4.【解析】【解答】解：A、∵∠B不是AB和AC的夹角，∠E不是DE和DF的夹角，不能证明△ABC≌△DEF， 故A错误；
B、∵在 △ABC≌△DEF中， ∴△ABC≌△DEF〔AAS〕， 故B正确；
C、∵在 △ABC≌△DEF中， ∴△ABC≌△DEF〔SAS〕， 故C正确；
D、∵在 △ABC≌△DEF中， ∴△ABC≌△DEF〔ASA〕， 故D正确；
综上，错误的选项是A.
故答案为：A.

【分析】三角形全等的判定定理有，SSS、SAS、AAS和ASA，其中两条边对应相等，一个角对应相等，那么这个角必须是这两条边的夹角。
5.【解析】【解答】解：AC边上的高是过B作直线AC的垂线，直角落在AC边上，只有C满足条件．故答案为：C．
【分析】根据三角形的高的意义可知，AC边上的高是过B作直线AC的垂线，垂足落在AC所在直线上.
6.【解析】【解答】解：当顶角=72°，底角=〔180°-72°〕÷2=54°，
当底角=72°，顶角=180°-72°×2=36°.
故答案为：C.

【分析】分两种情况求解，即当顶角为72°，或底角为72°，结合等腰三角形的性质和三角形内角和定理求解即可。
7.【解析】【解答】解：由题意可知DM垂直平分AB，
∴AD=BD，
∵△BDC的周长为BD+CD+BC=AD+CD+BC=AC+BC
∴△BCD的周长为5+3=8.
故答案为：A.
【分析】利用垂直平分线的性质可证得AD=BD，由此可证得△ACD的周长等于AC+BC，代入计算可求解。
8.【解析】【解答】解：如图，

∵ ，
∴∠1=∠F=45°，
又∵ ，
∴∠B=30°，
∴ ，
故答案为：B.
【分析】根据平行线的性质可得∠1=∠F=45°，再根据三角形内角与外角的关系可得∠1的度数.
9.【解析】【解答】解： ∵△ABC≌△DEF，
∴∠DEC=∠B=60°，DE=AB=4，
∴BC-BE=6-2=4，
∴DE=BC，
∴△DEC为等边三角形,
∴DC=EC=4.
故答案为：B.

【分析】由全等三角形的性质可得相关角相等，边相等，推出DE=BC，结合∠DEC=60°，可得△DEC为等边三角形, 从而求出DC的长.
10.【解析】【解答】解：如图，连接BD，

① 由作图可知，BA=BD，CA=CD，∴B和C在AD的垂直平分线上，即BH是AD的垂直平分线，故 ① ④ 正确；
② 无法判断AC平分  ，故② 错误；
③ ∵BH是AD的垂直平分线，∴AH⊥BC，∴   ，故 ③ 正确；
综上，正确的选项是 ①③④.
故答案为： C

【分析】由同圆的半径相等可得BA=BD，CA=CD，那么知B和C在AD的垂直平分线上，由于两点决定一条直线，可得BH是AD的垂直平分线，由于AH⊥BC，那么△ABC的面积为.
二、填空题〔此题有10小题，每题3分，共30分〕
11.【解析】【解答】解： ∵△ABC≌△DEF，
∴DE=AB=5.

【分析】由全等三角形的对应边相等可得DE和AB相等，那么知DE的长度.
12.【解析】【解答】解：∠BCD=∠A+∠B=60°+40°=100°.
故答案为：100.

【分析】利用三角形外角和定理即可直接求出∠BCD的大小.
13.【解析】【解答】解：设第三边长为x，
∵5-1 ∴4 ∵x为整数，
∴x=5.
故答案为：5.

【分析】根据三角形两边之和大于第三边，两边之差小于第三边，求出x的范围，结合第三边长为整数即可得出结果.
14.【解析】【解答】解：∵DE垂直平分AB，
∴AD=BD，∠A=90°-∠ADE=50°，
∴∠ABD=∠A=50°，
∵AB=AC，
∴∠C=〔180°-∠A〕÷2=〔180°-50〕÷2=65°，
∴∠DBC=∠ABC-∠ABD=65°-50°=15°.
故答案为：15.

【分析】利用垂直平分线的性质求出∠A和∠ABD的大小，再结合△ABC为等腰三角形，利用三角形内角和定理求出∠ABC的大小，那么∠DBE的度数可求.
15.【解析】【解答】解：假设∠ACB=∠DBC，
∵，
∴△ABC≌△DCB〔SAS〕；
假设AB=CD，
∵
∴△ABC≌△DCB〔SSS〕；
故答案为： ∠ACB=∠DBC或AB=CD .

【分析】现知两条边相等，根据边角边证明全等，可添此两条边的夹角相等；根据边边边证明全等可再添两条边相等.
16.【解析】【解答】解：∵EF∥BC，
∴∠BOE=∠CBO，
∵∠OBE=∠CBO，
∴∠BOE=∠OBE，
∴OE=BE=2，
同理OF=FC，
∴OF=EF-EO=6-2=4，
∴CF=OF=4.
故答案为：4.

【分析】根据平行线的性质定理，结合角平分线的定义求得OE=BE，OF=FC，那么OF的长度可求，从而求得FC的长.
17.【解析】【解答】解：如图，作CH⊥AB于H，

S△ACD：S△ABC=AD×CH：AB×CH=AD：AB=1:2，
∵S△ABC=100，
∴S△ACD=50.
故答案为：50.

【分析】由于△ABC和△ACD高都为CH，推得面积比等于底边之比，代入数据即可求值.
18.【解析】【解答】解：解：∠1+∠2=360°-〔∠B+∠C〕
=360°-〔180°-∠A〕
=360°-〔180°-60°〕
=240°.
故答案为：240.

【分析】利用四边形的内角和，再结合三角形的内角和把∠1+∠2转化为用含∠A的代数式表示，再代入∠A的值即可求得结果.
19.【解析】【解答】解：如图，取∠8,

∵正方形关于对角线对称，
∴∠1=∠8，
∵∠8+∠7=90°，
∴∠1+∠7=90°，
同理∠2+∠6=90°，∠3+∠5=90°，
∵∠4=45°，
∴ ∠1＋∠2＋∠3＋∠4＋∠5＋∠6＋∠7＝ 90°×3+45°=315°.
故答案为：315.

【分析】正方形是关于对角线对称的， 利用轴对称的性质推得∠1+∠7=90°，∠2+∠6=90°，∠3+∠5=90°，∠3+∠5=90°，结合∠4=45°，从而求得结果.
20.【解析】【解答】解： (1)、 ∵AB=AC，
∴∠ABC=∠C，
∴∠ABC=〔180°-108°〕÷2=36°，
∵BD平分∠ABC，
∴∠DBC=180°；
(2)、 在BC上截取BE=AB，

在△ABD和△EBD中，
∵
∴△ABD≌△EBD〔SAS〕，
∴∠BED=∠BAD=108°，∠BDE=∠ADB=180°-∠A-∠ABD=180°-108°-18°=54°，
∴∠CED=180°-∠BED=180°-108°=72°，∠CDE=180°-∠ADB-∠BDE=180°-54°-54°=72°，
∴∠CED=∠CDE，
∴CE=CD，
∴BC=BE+EC=AB+CD，
即BC-CD=AB或BC-AB=CD .
故答案为： BC=AB+CD或BC-CD=AB或BC-AB=CD .

【分析】〔1〕利用三角形内角和定理，结合等腰三角形的性质，先求得∠ABC的度数，再根据角平分线的定义即可求解；
〔2〕在BC上截取BE=AB，利用边角边定理证明△ABD≌△EBD，然后根据全等三角形对应角相等求出∠CED=∠CDE，那么可得出CE=CD，最后由线段之间的关系即可推出结果.
三、解答题〔此题有6小题；共40分〕
21.【解析】【分析】根据角平分线的作法作出AD即可；根据垂直平分线的作法作出MN即可.
22.【解析】【分析】先由∠1=∠2推得 ∠ CAB=∠ EAD ，然后利用边角边定理即可证明 △ABC≌△ADE .
23.【解析】【分析】〔1〕由平行线的性质可得 ∠B=∠C， 再由BE=CF，推得BF=CE，然后利用边角边定理证明 △ABF≌△DCE，那么对应边AF=DE；
〔2〕 由〔1〕知△ABF≌△DCE， 那么对应角 ∠AFB=∠DEC， 然后由邻补角的性质可得 ∠AFE=∠DEF， 那么由内错角相等判定AF∥DE.
24.【解析】【分析】由角平分线的定义求得 ∠EAC的度数，在直角△ADC中，由三角形内角和定理求得∠DAC的度数，那么由角的关系可求∠DAE的度数.
25.【解析】【分析】〔1〕由等边三角形的性质可得AB=BC，∠A=∠CBE，然后利用边角边定理可证△ABD≌△BCE，那么对应边BD=CE；
〔2〕由三角形外角的性质，结合全等三角形对应角相等，把∠DPC转化为 ∠ABD+∠PBC，那么可得出∠DPC为60°.
26.【解析】【分析】〔1〕由速度公式可得BP=2t, 那么可得出PC= 6﹣2t ；
〔2〕利用速度公式求得BP和CP的长度，结合D为AB的中点，推得BD=PC，BP=CQ，然后利用边角边定理证明△BPD和△CQP全等即可；
〔3〕 由于点P、Q的运动速度不相等，可得BP≠CQ，要使 △BPD≌△CPQ， 结合 ∠B=∠C，可得 BP和PC是对应边，CQ和BD是对应边， 那么BP和CQ的长度可求，再根据速度公式求速度即可.