2020-2021年浙江省嘉兴市九年级上学期数学第一次月考试卷及答案

这是一份2020-2021年浙江省嘉兴市九年级上学期数学第一次月考试卷及答案，共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

 九年级上学期数学第一次月考试卷
一、选择题
1.以下函数中，是二次函数的是(    )
A.                          B.                          C.                          D. 
A、 两种套餐，甲乙两人同去该食堂打饭，那么甲乙两人选择同款套餐的概率为〔　〕
A.                                          B.                                          C.                                          D. 
3.如图，点 、 、 在 上，假设 ，那么 的度数是〔    〕

A. 18°                                      B. 36°                                      C. 54°                                      D. 72° 
4.如图，在⊙O中，直径AB与弦MN相交于点P，∠NPB＝45°，假设AP＝2，BP＝6，那么MN的长为〔   〕

A.                                      B. 2                                      C. 2                                      D. 8
5.将抛物线 向上平移2个单位长度，再向右平移3个单位长度后，得到的抛物线解析式为〔   〕
A.               B.               C.               D. 
6.⊙O以原点为圆心，5为半径，点P的坐标为(4，2)，那么点P与⊙O的位置关系是(    )
A. 点P在⊙O内                B. 点P在⊙O上                C. 点P在⊙O外                D. 点P在⊙O上或⊙O外
7.如果关于二次函数 与x轴有公共点，那么m的取值范围是(   )
A.                                   B.                                   C.                                   D. 
8. 0≤x≤， 那么函数 的最大值为(    )
A. 0                                          B.                                           C. 1                                          D. 
9.同一坐标系中，抛物线y＝(x－a)2与直线y＝a＋ax的图象可能是(　　)
A.                                        B. 
C.                                           D. 
10.如图是二次函数 的图象的一局部，对称轴是直线 。

以下四个判断：① ；② ；③不等式 的解集是 ；④假设〔 ，y1〕，〔5，y2〕是抛物线上的两点，那么y1＜y2。其中正确的选项是〔    〕
A. ①②                                    B. ①④                                    C. ①③                                    D. ②③④
二、填空题
11.从装有a个球的暗袋中随机的摸出一个球，袋中有 个红球，通过大量重复的实验发现，摸到红球的频率稳定在 左右，可以估计a约为________．
12.二次函数 图像的对称轴是直线________。
13.一抛物线的形状，开口方向与 相同，顶点在(-2，3)，那么此抛物线的解析式为________．
14.如图，经过原点的⊙P与x、y轴分别交于A、B两点，点C是劣弧OB上一点，那么∠ACB度数为________.

15.定义：给定关于 的函数 ，对于函数图象上的任意两点( ， )，( ， )，当 时，都有 ，那么称该函数为减函数．根据以上定义，以下函数为减函数的有________．(只需填写序号)
① ；② ；③ ；④
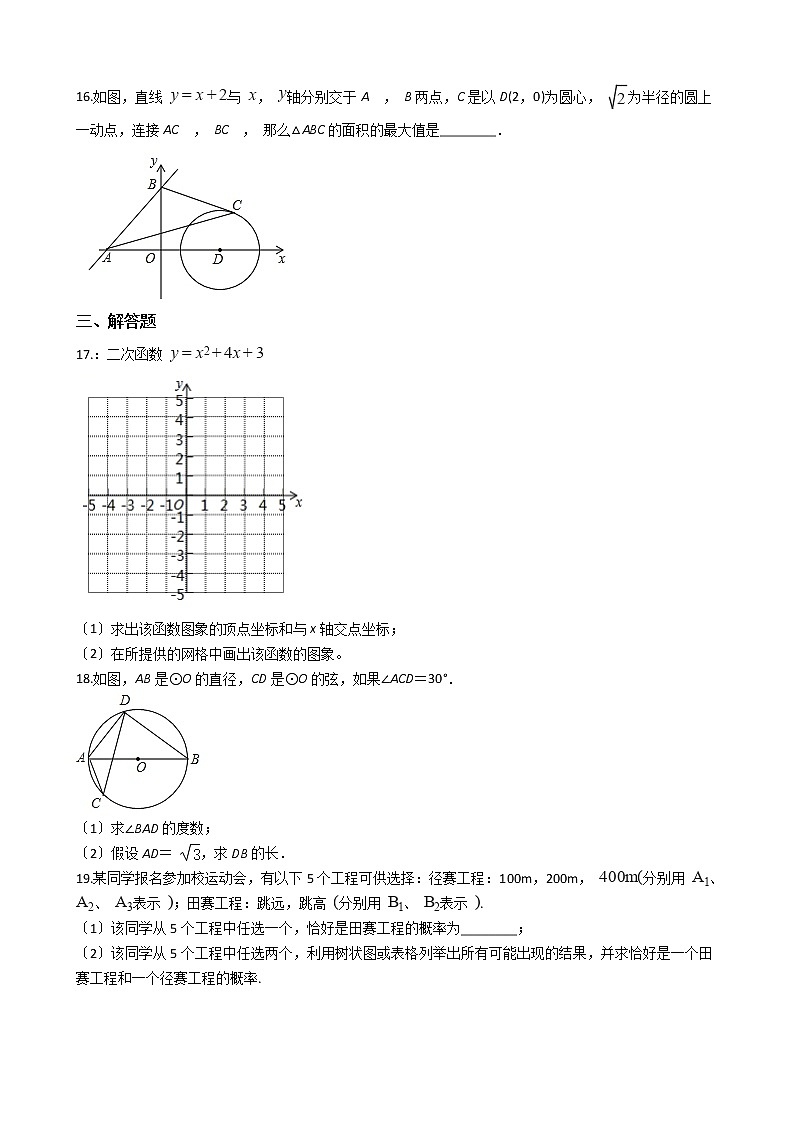
16.如图，直线 与 ， 轴分别交于A ， B两点，C是以D(2，0)为圆心， 为半径的圆上一动点，连接AC ， BC ， 那么△ABC的面积的最大值是________．

三、解答题
17.：二次函数

〔1〕求出该函数图象的顶点坐标和与x轴交点坐标；
〔2〕在所提供的网格中画出该函数的图象。
18.如图，AB是⊙O的直径，CD是⊙O的弦，如果∠ACD＝30°．

〔1〕求∠BAD的度数；
〔2〕假设AD＝ ，求DB的长．
19.某同学报名参加校运动会，有以下5个工程可供选择：径赛工程：100m，200m， 分别用 、 、 表示 ；田赛工程：跳远，跳高 分别用 、 表示 .
〔1〕该同学从5个工程中任选一个，恰好是田赛工程的概率为________；
〔2〕该同学从5个工程中任选两个，利用树状图或表格列举出所有可能出现的结果，并求恰好是一个田赛工程和一个径赛工程的概率.
20.在一次篮球比赛中，如图，队员甲正在投篮．球出手时离地面 m，与篮圈中心的水平距离为7m，球出手后水平距离为4m时到达最大高度4m，设篮球运行轨迹为抛物线，篮圈距地面3m.
 
〔1〕建立如以下列图的平面直角坐标系，问此球能否准确投中？
〔2〕此时，对方队员乙在甲面前1m处跳起盖帽拦截，乙的最大摸高为3.1m，那么他能否获得成功？
21.如图，△ABC是⊙O的内接三角形，点C是优弧AB上一点〔点C不与点A ， B重合〕，设∠OAB=α ， ∠C=β ．

〔1〕当α=40°时，求β的度数；
〔2〕猜想α与β之间的关系，并给予证明．
22.为了落实国务院的指示精神，某地方政府出台了一系列“三农〞优惠政策，使农民收入大幅度增加.某农户生产经销一种农产品，这种产品的本钱价为每千克20元，市场调查发现，该产品每天的销售量y〔千克〕与销售价x〔元/千克〕有如下关系：
y＝-2x+80．设这种产品每天的销售利润为w元．
〔1〕该产品销售价定为每千克多少元时，每天的销售利润最大？最大利润是多少元？
〔2〕如果物价部门规定这种产品的销售价不高于每千克28元，该农户想要每天获得150元的销售利润，销售价应定为每千克多少元？
23.好山好水好嘉兴，石拱桥在嘉兴处处可见，小明要帮助船夫计算一艘货船是否能够平安通过一座圆弧形的拱桥，现测得桥下水面AB宽度16m时，拱顶高出水平面4m，货船宽12m，船舱顶部为矩形并高出水面3m。 

〔1〕请你帮助小明求此圆弧形拱桥的半径；
〔2〕小明在解决这个问题时遇到困难，请你判断一下，此货船能顺利通过这座拱桥吗？说说你的理由.
24.如图，直线 与抛物线 交于点A ， B ， 点A在 轴上，点B在 轴上．

〔1〕求该抛物线的解析式．
〔2〕点P是直线AB上方的抛物线上的一动点，假设S△AOB∶S△PAB＝8∶3，求此时点P的坐标．
〔3〕点E是抛物线对称轴上的动点，点F是抛物线上的点，判断有几个位置能够使得点E ， F ， B ， O为顶点的四边形是平行四边形，直接写出相应的点F的坐标．

答案解析局部
一、选择题
1.【解析】【解答】解：A、不是二次函数，故A不符合题意；
B、y=2x2-x-1是二次函数，故B符合题意；
C、是反比例函数不是二次函数，故C不符合题意；
D、y=x+2是一次函数，不是二次函数，故D不符合题意；
故答案为：B.
【分析】形如y=ax2+bx+c〔a，b，c是常数，a≠0〕的函数是二次函数，再对各选项逐一判断。
2.【解析】【解答】解：树状图如下

一共有4种结果，甲乙两人选择同款套餐的有2种情况，
∴P〔甲乙两人选择同款套餐〕=.
故答案为：A.
【分析】由题意可知此事件是抽取放回，列出树状图，根据树状图可得到所有等可能的结果数及甲乙两人选择同款套餐的情况数，然后利用概率公式可求解。
3.【解析】【解答】解：∵
∴∠BAC=∠BOC=×72°=36°
故答案为：B.
【分析】利用一条弧所对的圆周角等于它所对的圆心角的一半，就可求出∠BAC的度数。
4.【解析】【解答】解：过点O作OD⊥MN于点D，连接ON，那么MN＝2DN，

∵AB是⊙O的直径，AP＝2，BP＝6，
∴⊙O的半径＝ 〔2+6〕＝4，
∴OP＝4﹣AP＝4﹣2＝2，
∵∠NPB＝45゜，
∴△OPD是等腰直角三角形，
∴OD＝ ，
在Rt△ODN中，
DN＝ ，
∴MN＝2DN＝2 ．
故答案为：C．
【分析】过点O作OD⊥MN于点D，连接ON，根据垂径定理得出MN＝2DN，然后根据线段的和差算出OP的长，根据等腰直角三角形的性质求出OD的长，在Rt△ODN中，根据勾股定理算出DN的长，从而即可得出答案。
5.【解析】【解答】将 化为顶点式，得 .将抛物线 向上平移2个单位长度，再向右平移3个单位长度后，得到的抛物线的解析式为 ，
故答案为：B.

【分析】由题意先将抛物线的解析式根据公式y=a(x+)2+配成顶点式，再根据平移规律“左加右减、上加下减〞可求解。
6.【解析】【解答】解：OP=， ∵， ， ∴点P在⊙O内，
故答案为A。
【分析】首先利用勾股定理算出点P到圆心的距离，再比较这个距离与该圆的半径的大小即可得出结论。
7.【解析】【解答】解：∵ 关于二次函数 与x轴有公共点
∴b2-4ac≥0即.
解之：m≤5.
故答案为：D.
【分析】由二次函数与x轴有公共点，可得b2-4ac≥0，由此建立关于m的不等式，解不等式即可。
8.【解析】【解答】解：y=-〔x-2〕2+1
∵a=-1＜0
∴当x＜2时y随x的增大而增大，
∵0≤x≤
∴当x=时，y有最大值为.
故答案为：B.
【分析】将函数解析式转化为顶点式，利用二次函数的性质可知当x＜2时y随x的增大而增大，再根据x的取值范围可知当x=时，y有最大值，然后代入计算可求出最值。
9.【解析】【解答】解：当a＞0时，二次函数y=〔x-a〕2的顶点坐标在x轴的正半轴；y=a+ax的图像经过第一，二，三象限，
故答案为：D.
【分析】分情况讨论：当a＞0和a＜0，二次函数的顶点坐标所在的位置及一次函数图像经过的象限，即可得出答案。
10.【解析】【解答】解：∵抛物线与x轴有两个交点，
∴b2-4ac＞0，即b2＞4ac，故①正确；
∵抛物线的对称轴为直线x=0，抛物线与x轴的一个交点横坐标大于2，
∴当x=2时，4a-2b+c＞0，故②错误；
设抛物线与x轴的两交点的横坐标为m，n〔m＜n〕
当x＜m或x＞n时，ax2+bx+c＞0，故③错误；
∵假设〔 ，y1〕，〔5，y2〕是抛物线上的两点，
∵a＞0，当x＞1时，y随x的增大而增大
当x=-1和x=3时函数值相等，
∴3＜5
∴y1＜y2 ， 故④正确；
正确的有①④.
故答案为：B.
【分析】根据抛物线与x轴的交点个数可对①作出判断；利用抛物线的对称轴为直线x=0，抛物线与x轴的一个交点横坐标大于2，可对②作出判断；观察x轴上方的图像，可得到x的取值范围，可对③作出判断；观察图像，可知当x=-1和x=3时函数值相等，可对④作出判断，综上所述可得到正确结论的个数。
二、填空题
11.【解析】【解答】解：由题意得

解之：a=20.
故答案为：20.
【分析】利用频率=频数÷总数，列方程求解即可。
12.【解析】【解答】解：y=x2+2x+3=〔x+1〕2+2，
∴此二次函数的对称轴为直线x=1.
故答案为：x=1.
【分析】利用配方法将函数解析式转化为顶点式，就可得到此二次函数的对称轴。
13.【解析】【解答】解：∵ 一抛物线的形状，开口方向与 相同， 顶点在(-2，3)
∴此函数解析式为 .
故答案为：.

【分析】由题意可知所求抛物线的顶点坐标及a的值，即可得到此函数解析式。
14.【解析】【解答】解：∵
∴∠AOB=∠ACB=90°.
故答案为：90°.

【分析】利用同弧所对的圆周角相等，就可求出∠ACB的度数。
15.【解析】【解答】解：①y＝−2x＋1，k＝−2＜0，y随x的增大而减小，故①正确；
②y＝3x，k＝3＞0，y随x的增大而增大，故②错误；
③y＝， y随x的增大而减小，
当x1＜0，x2＞0时，y1＜y2 ， 故③错误；
④y＝5x2 ， a＝5＞0开口向上，x＜0时，y随x的增大而减小，故④正确；
故答案为：①④．
【分析】利用一次函数的增减性可对①②作出判断；利用反比例函数的性质，可对③作出判断；再利用二次函数的性质，可对④作出判断，由此可得答案。
16.【解析】【解答】解：过点D作DH⊥AB于点H，延长HD交圆于点C1.

∵△ABC的边BAB时定值，当△ABC的AB边上的高最长时，此时△ACB的面积最大
当x=0时y=2；当y=0时x=-2,
∴点A〔-2，0〕，点B〔0，2〕
∴OA=OB=2
∴
∴∠BAO=45°
∴△AHD是等腰直角三角形，
∵点D〔2，0〕
∴AD=|-2-2|=4
∴DH=ADsin45°=；
∵圆的半径为
∴C1H=
∴.
故答案为：6.
【分析】过点D作DH⊥AB于点H，延长HD交圆于点C1 ， △ABC的边BAB时定值，当△ABC的AB边上的高最长时即C1H的值最大，此时△ACB的面积最大；利用函数解析式求出点A，B的坐标，由此可求出OA，OB的长，再利用勾股定理求出AB的长，同时可证得△AHD是等腰直角三角形，利用解直角三角形求出DH的长；然后利用三角形的面积公式可求出△ABC的最大面积。
三、解答题
17.【解析】【分析】〔1〕将函数解析式转化为顶点式，可得到抛物线的顶点坐标；再由y=0建立关于x的方程，解方程求出x的值，可得到抛物线与x轴的交点坐标。
〔2〕利用顶点坐标，图像与x轴的交点坐标及与y轴的交点坐标，先描点，再用圆滑的曲线连接即可。
18.【解析】【分析】连接OD，利用圆周角定理求出∠AOD的度数，再根据有一个角是60°的等腰三角形是等边三角形，可证得△AOD是等边三角形，利用等边三角形的性质可求出∠BAD的度数。
〔2〕利用等边三角形的性质可求出AB的长，再利用圆周角定理可证得△ABD是直角三角形，然后利用解直角三角形求出BD的长。
19.【解析】解：〔1〕∵5个工程中田赛工程有2个，∴该同学从5个工程中任选一个，恰好是田赛工程的概率为： .
故答案为： ；

【分析】〔1〕根据简单概率的公式即可求解；
〔2〕由题意先画出树状图，由树状图的信息可知， 共有20种等可能的结果，恰好是一个田赛工程和一个径赛工程的有12种情况，那么恰好是一个田赛工程和一个径赛工程的概率可求解。
20.【解析】【分析】〔1〕由可得到抛物线的顶点坐标及经过 (0，) ，利用待定系数法求出此函数解析式，再将x=7代入函数解析式求出对应的函数值，即可做出判断。
〔2〕比较大小，可作出判断。
21.【解析】【分析】〔1〕连接OB，利用等腰三角形的性质及三角形内角和定理求出∠AOB的度数，然后利用一条弧所对的圆周角等于圆心角的一半，就可求出∠C的度数。
〔2〕利用三角形的内角和定理用含α的代数式表示出∠AOB；再利用圆周角定理可得到α与β之间的关系。
22.【解析】【分析】〔1〕利用销售利润W=每千克的利润×销售量，列出W与x之间的函数解析式，再将函数解析式转化为顶点式，利用二次函数的性质可求出最大利润。
〔2〕由W=150建立关于x的方程，解方程求出x的值，再根据规定这种产品的销售价不高于每千克28元，可得到此销售价格。
23.【解析】【分析】〔1〕连接OA，利用垂径定理求出AD的长，设OA=r，那么OD=r-4，利用勾股定理建立关于r的方程，解方程求出r的值。
〔2〕利用垂径定理求出FG的长，利用勾股定理求出OG的长，从而可得到OD的长，然后求出DG的长，再与3比较大小，可作出判断。
24.【解析】【解答】解：〔3〕抛物线 的对称轴为
根据平行四边形的定义，分以下两种情况： 
①当OB为平行四边形的一条边时
此时，有以下两种情况，如图2所示：


那么点 的横坐标为 ，将其代入抛物线的解析式得：
即点 的坐标为
点 的横坐标为 ，将其代入抛物线的解析式得：
即点 的坐标为
②当OB为平行四边形的一条对角线时，如图3所示：

为平行四边形


过点 分别作x轴的平行线，分别交y轴和y轴的平行线与点M、N
，即
又


那么点 的横坐标为 ，将其代入抛物线的解析式得：
即点 的坐标为
综上，点F的坐标为 或 或 ．     

【分析】〔1〕利用一次函数解析式求出点A，B的坐标，再利用待定系数法求出二次函数解析式。
〔2〕利用点A，B的坐标，可求出△AOB的面积，结合条件求出△PBA的面积； 如图1，过点P作 轴，交AB于点C，利用函数解析式设点P，C的坐标，利用含a的代数式表示出PC的长，再利用△PAB的面积建立关于a的方程，解方程求出a的值；再分别求出当a=1和当a=3时的y的值，即可得到点P的坐标。
〔3〕利用函数解析式求出抛物线的对称轴，根据平行四边形的定义，分情况讨论：①当OB为平行四边形的一条边时，利用求出点F1 ， F2的横坐标及纵坐标，就可的点F1 ， F2的坐标，；②当OB为平行四边形的一条对角线时，利用平行四边形的性质及全等三角形的性质求出F3的坐标，综上所述可得到符合题意的点F的坐标。