2020-2021学年天津市武清区英华国际中学七上期末数学试卷

这是一份2020-2021学年天津市武清区英华国际中学七上期末数学试卷，共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共12小题；共60分）
1. 如果升降机下降 10 米记作 −10 米，那么上升 15 米记作 米．
A. −15B. +15C. +10D. −10

2. 绝对值大于 1 而小于 4 的整数有 个．
A. 1B. 2C. 3D. 4

3. 下列判断正确的是
A. x2y2 的次数是 2B. 0 不是单项式
C. 23πa2b 的系数是 23D. 3x4+2x2−6 是四次三项式

4. 将一副直角三角尺按如图所示的不同方式摆放，则图中锐角 ∠α 与 ∠β 相等的是
A. B.
C. D.

5. 《算法统宗》是我国古代数学著作，其中记载了一道数学问题大意如下：若将绳子三折后测井深则多 4 尺；若将绳子四折去测井深则多 1 尺．问绳长和井深各多少尺?设井深为 x 尺，则可列方程为
A. 3x+4=4x+1B. 3x+4=4x+1
C. 3x−4=4x−1D. x3−4=x4−1

6. 已知 ∠α=27ʹ，∠β=0.45∘，则 ∠α 与 ∠β 的大小关系是
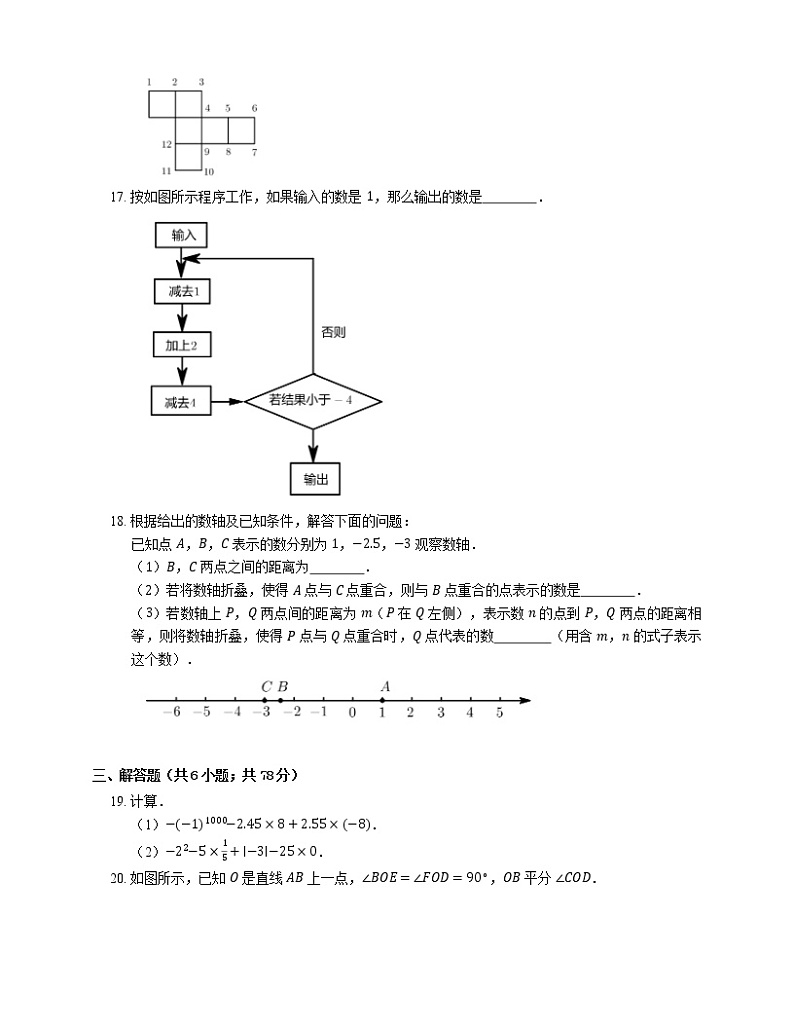
A. ∠α=∠βB. ∠α>∠βC. ∠α<∠βD. 无法确定

7. 如图所示，射线 OC 的端点 O 在直线 AB 上，∠AOC 的度数比 ∠BOC 的 2 倍多 10∘．设 ∠AOC 和 ∠BOC 的度数分别为 x∘，y∘，则可列方程组为
A. x+y=180,x=y−10B. x+y=180,x=2y+10C. x+y=180,x=10−2yD. x+y=90,x=2y−10

8. 如图，B，C 两点把线段 MN 分成三部分，其比为 MB:BC:CN=2:3:4，点 P 是 MN 的中点，PC=2 cm，则 MN 的长为
A. 30 cmB. 36 cmC. 40 cmD. 48 cm

9. 钟表上 8 点 30 分时，时针与分针的夹角为
A. 15∘B. 30∘C. 75∘D. 60∘

10. 如图，直线 AB 与 CD 相交于点 O，∠DOE=α，∠DOF:∠AOD=2:3，射线 OE 平分 ∠BOF，则 ∠BOC=
A. 540∘−5αB. 540∘−6αC. 30∘D. 40∘

11. 若 ab≠0，那么 ∣a∣a+∣b∣b 的取值不可能是
A. −2B. 0C. 1D. 2

12. 线段 AB，点 P 是直线 AB 上一点，直线上共有 3 条线段：AB，PA 和 PB，若其中有一条线段的长度是另一条线段长度的两倍，则称点 P 是线段 AB 的“巧分点”，线段 AB 的“巧分点”的个数是
A. 6B. 8C. 9D. 10

二、填空题（共6小题；共30分）
13. 据有关报道，2020 年某市斥资约 5800000 元改造老旧小区，数据 5800000 用科学记数法表示为 ．

14. 设 a，b 互为相反数，c，d 互为倒数，则 2021a+b−2020cd 的值是 ．

15. 直线 AB，BC，CA 的位置关系如图所示，则下列语句：①点 B 在直线 BC 上；②直线 AB 经过点 C；③直线 AB，BC，CA 两两相交；④点 B 是直线 AB，BC 的交点，以上语句正确的有 （只填写序号）．

16. 如图是一个正方体纸盒的展开图，当折成纸盒时，与数 11 重合的数是 ．

17. 按如图所示程序工作，如果输入的数是 1，那么输出的数是 ．

18. 根据给出的数轴及已知条件，解答下面的问题：
已知点 A，B，C 表示的数分别为 1，−2.5，−3 观察数轴．
（1）B，C 两点之间的距离为 ．
（2）若将数轴折叠，使得 A 点与 C 点重合，则与 B 点重合的点表示的数是 ．
（3）若数轴上 P，Q 两点间的距离为 m（P 在 Q 左侧），表示数 n 的点到 P，Q 两点的距离相等，则将数轴折叠，使得 P 点与 Q 点重合时，Q 点代表的数 （用含 m，n 的式子表示这个数）．

三、解答题（共6小题；共78分）
19. 计算．
（1）−−11000−2.45×8+2.55×−8．
（2）−22−5×15+∣−3∣−25×0．

20. 如图所示，已知 O 是直线 AB 上一点，∠BOE=∠FOD=90∘，OB 平分 ∠COD．
（1）图中有与 ∠DOE 相等角 ．
（2）图中与 ∠DOE 互余的角有 ．
（3）图中与 ∠DOE 互补的角有 ．

21. 先化简，再求值：2a2b−ab2−3a2b−1+2ab2+1，其中 a=2，b=14．

22. 解方程或方程组．
（1）解方程 210−0.5y=−1.5y+2．
（2）解方程组 2x−y3−x+y4=−1,6x+y−42x−y=16.

23. 整理一批图书，由一个人做要 40 小时完成，现计划由一部分人先做 4 小时，再增加 2 人和他们一起做 8 小时，完成这项工作．假设这些人的工作效率相同，具体应先安排多少人工作?

24. 已知点 C 在线段 AB 上，AC=2BC，点 D，E 在直线 AB 上，点 D 在点 E 的左侧．若 AB=18，DE=8，线段 DE 在线段 AB 上移动．
（1）如图 1，当 E 为 BC 中点时，求 AD 的长．
（2）点 F（异于 A，B，C 点）在线段 AB 上，AF=3AD，CE+EF=3，求 AD 的长．
答案
第一部分
1. B
2. D【解析】绝对值大于 1 而小于 4 的整数有：±2，±3，共有 4 个．
3. D【解析】A选项：x2y2 的次数是 4，不是 2，故A选项错误；
B选项：由于单独的数是单项式，因此 0 是单项式，故B选项错误；
C选项：23πa2b 的系数为 23π，不是 23，故C选项错误；
D选项：3x4+2x2−6 是四次三项式，故D选项正确．
4. B【解析】A，由图形得：α+β=90∘，不合题意；
B，由图形得：β+γ=α+γ=90∘，
可得 β=α，符合题意；
C，由图形可得：α=β=180∘−45∘=135∘，不是锐角，不符合题意；
D，由图形得：α+45∘=90∘，β+30∘=90∘，可得 α=45∘，β=60∘，不合题意，故选B．
5. A
【解析】根据题意可得等量关系：3井深+4=4井深+1，
根据等量关系列出方程即可．
设井深为 x 尺，由题意得：3x+4=4x+1．
6. A【解析】方法一：27÷60=0.45，故 27ʹ=0.45∘．
∴∠α=∠β．
方法二：∠α=27ʹ，
∠β=0.45∘=27ʹ．
故 ∠α=∠β．
7. B
8. B【解析】由 MB:BC:CN=2:3:4，
设 MB 为 2xx>0，BC 为 3x，CN 为 4x，
则 MN=MB+BC+CN=9x，
因为 P 是 MN 的中点，
所以 PN=12MN，
所以 PC=PN−CN=12MN−CN，
即 12×9x−4x=2，
解得 x=4，
所以 MN=9x=36，
故 MN 的长为 36 cm．
9. C【解析】∵8 点 30 分，时针在 8 和 9 正中间，分针指向 6，
中间相差两个半大格，而钟表 12 个数字，每相邻两个数字之间的夹角为 30∘，
∴8 点 30 分时，时针与分针的夹角的度数为：30∘×2.5=75∘．
10. B
【解析】设 ∠DOF=2x，∠AOD=3x，
∵∠DOE=α，
∴∠FOE=α−2x，
∵ 射线 OE 平分 ∠BOF，
∴∠BOE=∠EOF=α−2x，
则：3x+α+α−2x=180∘，
解得：x=180∘−2α，
∴∠AOD=3×180∘−2α=540∘−6α，
∴∠BOC=540∘−6α．
11. C【解析】方法一：当 a，b 两个都为正数，∣a∣a+∣b∣b=1+1=2，
当 a，b 中有一个正数一个负数时，∣a∣a+∣b∣b=1+−1=0，
当 a，b 两个都为负数，∣a∣a+∣b∣b=−1+−1=−2，
都不可能为 1．
方法二：
∵ab≠0，
∴a≠0 且 b≠0，
①当 a>0，b>0 时，
∣a∣a+∣b∣b=aa+bb=1+1=2，故D项正确；
②当 a>0，b<0 时，
∣a∣a+∣b∣b=aa+−bb=1+−1=1−1=0，故B项正确；
③当 a<0，b>0 时，
∣a∣a+∣b∣b=−aa+bb=−1+1=0，故B项正确；
④当 a<0，b<0 时，
∣a∣a+∣b∣b=−aa+−bb=−1+−1=−2，故A项不正确．
12. C【解析】根据巧分点的定义进行分类讨论：
当点 P 在直线 AB 上且在点 A 的左侧时可以有：PA=2AB，PB=2PA（或 PB=2AB），AB=2PA；
当点 P 在线段 AB 上时可以有 PA=2PB，PB=2PA，AB=2PA（或 AB=2PB）；
当点 P 在直线 AB 上且在点 B 的右侧时可以有：PB=2AB，PA=2AB（或 PA=2AB），AB=2PB；
综上所述，共有 9 个巧分点．
第二部分
13. 5.8×106
【解析】数据 5800000 用科学记数法表示为：5.8×106．
14. −2020
【解析】∵a，b 互为相反数，cd 互为倒数，
∴a+b=0，cd=1，
∴2021a+b−2020cd=0−2020=−2020．
15. ①③④
【解析】由题中所给图，知点 B 在直线 BC 上，故①正确；
AB 并不过点 C，故②错误；
AB 与 BC 交于点 B，AB 与 CA 交于点 A，BC 与 CA 交于点 C，故③④正确．
16. 1，7
【解析】通过折叠正方体的折叠图发现，折成纸盒时，数字 1，7 以及 11 会重合在同一点上．
17. −5
【解析】把 x=1 代入计算程序中得：1−1+2−4=−2>−4，
把 x=−2 代入计算程序中得：−2−1+2−4=−5<−4，
则输出结果为 −5．
18. 0.5，0.5，m2+n
【解析】（1）BC=−2.5−−3=0.5．
（2）∵A 点和 C 点重合，
∴ 中点为 −1．
故 B 点对应点：−2−−2.5=0.5．
（3）设 P，Q 对应的分别为 x，y，
由题意知：x+y2=n,y−x=m,
解得 x=n−m2,y=m2+n.
第三部分
19. （1） 原式=−1−8×2.45+2.55=−1−8×5=−1−40=−41.
（2） 原式=−4−1+3−0=−5+3=−2.
20. （1） ∠AOF
【解析】
∵∠BOE=90∘，
∴∠BOE=∠3+∠4=90∘，
∵∠FOD=90∘，
∴∠FOD=∠2+∠3=90∘，
∴∠2+∠3=∠3+∠4=90∘，
∴∠2=∠4，即 ∠EOF=∠BOD，
∵∠BOE=90∘，
∴∠AOE=180∘−∠BOE=90∘，
∴∠1+∠2=∠AOE=90∘=∠2+∠3，
∴∠1=∠3，即 ∠DOE=∠AOF．
（2） ∠EOF，∠BOD，∠BOC
【解析】由（1）可知，∠2+∠3+∠4=90∘，
∵OB 平分 ∠COD，
∴∠4=∠5，
∴∠3+∠5=90∘（等角的余角相等），
即 ∠3 和 ∠2，∠4，∠5 互余，
即与 ∠DOE 互余的角有 ∠EOF，∠BOD，∠BOC．
（3） ∠BOF
【解析】由（1）可知，∠3=∠1，
又 ∵∠3+∠BOF=∠1+∠BOF=180∘（AB 是直线），
∴∠DOE 和 ∠BOF 互补．（等角的补角相等）
21. 原式=2a2b−2ab2−3a2b+3+2ab2+1=−a2b+4,
将 a=2，b=14 代入 原式=−22×14+4=3．
22. （1）
210−0.5y=−1.5y+2.
去括号，得：
20−y=−1.5y−2.
移项，得：
−y+1.5y=−2−20.
合并，得：
0.5y=−22.
解得：
y=−44.
（2）
2x−y3−x+y4=−1,6x+y−42x−y=16.
8x−y−3x+y=−12,6x+y−42x−y=16.
5x−11y=−12, ⋯⋯①−2x+10y=16. ⋯⋯②
① ×2+ ② ×5 得
28y=56.y=2.
把 y=2 代入②得
x=2.
所以 x=2,y=2.
23. 设应先安排 x 人工作，
4x40+8x+240=1,
解得：
x=2,
答：应先安排 2 人工作．
24. （1） ∵AB=18，AC=2BC，
∴AC=12，BC=6，
又 ∵E 为 BC 中点，
∴CE=12BC=3，
∵DE=8，
∴CD=DE−CE=8−3=5，
∴AD=AC−CD=12−5=7．
（2） ①如图 3，
∵AF=3AD，DF=2AD，
当 E 在线段 AC 上时，DE=8，AC=12，此时 F 在线段 DE 上，
设 AD=x，则 DF=2x，EF=DE−DF=8−2x，CE=4−x，
∴8−2x+4−x=3，
则 x=3，
∴AD=3；
②如图 4，
设 AD=x，则 DF=2x，EF=2x−8，CE=x−4，
∴3x−12=3，
则 x=5，
∴AD=5，
∴ 综上所述，AD=3或5．