2020年北京市平谷区中考一模数学试题

这是一份2020年北京市平谷区中考一模数学试题，共16页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共8小题；共40分）
1. 面对突如其来的疫情，全国广大医务工作者以白衣为战袍，义无反顾的冲在抗疫战争的一线，用生命捍卫人民的安全．据统计，全国共有 346 支医疗队，将近 42600 名医护工作者加入到支援湖北武汉的抗疫队伍，将 42600 用科学计数法表示为
A. 0.426×105B. 4.26×104C. 42.6×103D. 426×102

2. 剪纸是我们国家特别悠久的民间艺术形式之一，它是人们用祥和的图案企望吉祥、幸福的一种寄托．下列剪纸图形中，既是轴对称图形又是中心对称图形的是
A. B.
C. D.

3. n 边形的内角和为 1800∘，则该 n 边形的边数为
A. 12B. 10C. 8D. 6

4. 若已知实数 a，b 满足 ab<0，且 a+b>0，则 a，b 在数轴上的位置正确的是
A. B.
C. D.

5. 已知锐角 ∠AOB．如图，
（1）在射线 OA 上取一点 C，以点 O 为圆心，OC 长为半径作弧 DE，交射线 OB 于点 F，连接 CF；
（2）以点 F 为圆心，CF 长为半径作弧，交弧 DE 于点 G；
（3）连接 FG，CG．作射线 OG．
根据以上作图过程及所作图形，下列结论中错误的是
A. ∠BOG=∠AOBB. 若 CG=OC，则 ∠AOB=30∘
C. OF 垂直平分 CGD. CG=2FG

6. 如果 m−n−3=0，那么代数式 m2n−n⋅nm+n 的值为
A. 3B. 2C. −3D. −2

7. 如图是 6×6 的正方形网格，点 A，B 均在格点上．如果点 C 也在此正方形网格的格点上，且 ∠ACB=90∘，则满足条件的点 C 共有
A. 3 个B. 4 个C. 6 个D. 8 个

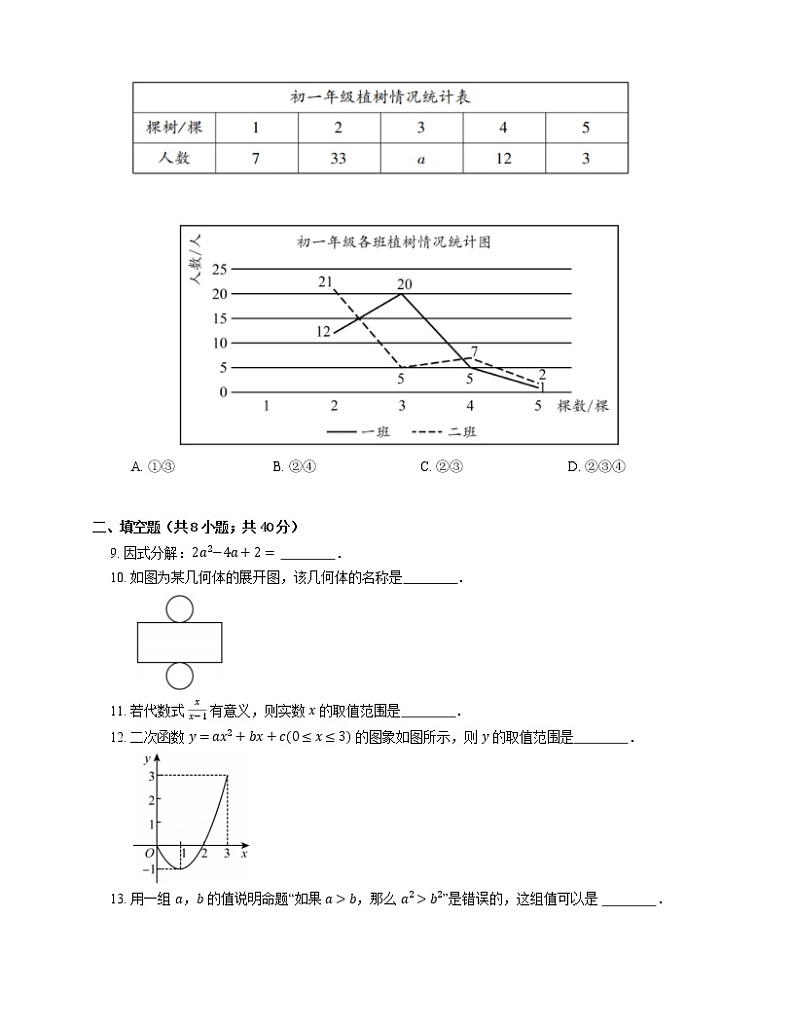
8. 某校在“爱护地球，绿化祖国”的活动中，组织同学开展植树造林活动，为了了解同学的植树情况，学校抽查了初一年级所有同学的植树情况（初一年级共有两个班），并将调查数据整理绘制成如下所示的部分数据尚不完整的统计图表．下面有四个推断：
① a 的值为 20；
②初一年级共有 80 人；
③一班植树棵树的众数是 3；
④二班植树棵树的是中位数 2．
其中合理的是
A. ①③B. ②④C. ②③D. ②③④

二、填空题（共8小题；共40分）
9. 因式分解：2a2−4a+2= ．

10. 如图为某几何体的展开图，该几何体的名称是 ．

11. 若代数式 xx−1 有意义，则实数 x 的取值范围是 ．

12. 二次函数 y=ax2+bx+c0≤x≤3 的图象如图所示，则 y 的取值范围是 ．

13. 用一组 a，b 的值说明命题“如果 a>b，那么 a2>b2”是错误的，这组值可以是 ．

14. 如图，矩形 ABCD 中，AB=3，BC=6，点 E，F 是 BC 的三等分点，连接 AF，DE，相交于点 M，则线段 ME 的长为 ．

15. 我国古代数学著作《孙子算经》中记载了这样一个有趣的数学问题“今有五等诸侯，共分橘子 60 颗，人别加三颗，问五人各得几何?”题目大意是：诸侯 5 人，共同分 60 个橘子，若后面的人总比前一个人多分 3 个，问每个人各分得多少个橘子?若设中间的那个人分得 x 个，依题意可列方程得 ．

16. 某公司计划招募 10 名技术人员，他们对 20 名面试合格人员进行了测试，测试包括理论知识和实践操作两部分，20 名应聘者的成绩排名情况如图所示．下面有 3 个推断：
①甲测试成绩非常优秀，入选的可能性很大；
②乙的理论知识排名比实践操作排名靠前；
③位于椭圆形区域内的应聘者应该加强该专业理论知识的学习．
其中合理的是 （写序号）．

三、解答题（共12小题；共156分）
17. 计算：3tan30∘−π−40+12−1+3−2．

18. 解不等式组：4x−1x.

19. 如图，OG 平分 ∠MON，点 A 是 OM 边上一点，过点 A 作 AB⊥OG 于点 B，C 为线段 OA 中点，连接 BC．求证：BC∥ON．

20. 关于 x 的一元二次方程 x2−2kx+k2+k−2=0 有两个不相等的实数根．
（1）求 k 的取值范围；
（2）若 k 为正整数，求 k 的值及此时方程的根

21. 如图，矩形 ABCD 的对角线 AC，BD 相交于点 O，过 B 点作 BF∥AC，过 C 点作 CF∥BD，BF 与 CF 相交于点 F．
（1）求证：四边形 BFCO 是菱形；
（2）连接 OF，DF，若 AB=2，tan∠OFD=23，求 AC 的长．

22. 如图，等边 △ABC，作它的外接圆 ⊙O，连接 AO 并延长交 ⊙O 于点 D，交 BC 于点 E，过点 D 作 DF∥BC，交 AC 的延长线于点 F．
（1）依题意补全图形并证明：DF 与 ⊙O 相切；
（2）若 AB=6，求 CF 的长．

23. 在平面直角坐标系中，反比例函数 y=kxx>0 的图象 G 与直线 l:y=2x−4 交于点 A3,a．
（1）求 k 的值；
（2）已知点 P0,nn>0，过点 P 作平行于 x 轴的直线，与图象 G 交于点 B，与直线 l 交于点 C．横、纵坐标都是整数的点叫做整点．记图象 G 在点 A，B 之间的部分与线段 AC，BC 围成的区域（不含边界）为 W．
①当 n=5 时，直接写出区域 W 内的整点个数；
②若区域 W 内的整点恰好为 3 个，结合函数图象，直接写出 n 的取值范围．

24. 2013 年 11 月，习近平同志到湖南湘西考察时，首次作出了“实事求是、因地制宜、分类指导、精准扶贫”的重要指示．精准扶贫一方面要为贫困把脉，找准原因．各省各地区分别对建档立卡的贫困人员进行摸底调查．如图 1 为某省 2013 年底随机抽取 40000 名建档立卡的贫困人员，对他们的致贫原因进行了抽样调查的问卷结果．另一方面，精准扶贫要对症下药，2013 至 2018 年，中央财政安排专项扶贫资金从 394 亿元增加到 1060 亿元，累计投入 3882 亿元；加大贫困地区基础设施建设，进一步完善医疗保险制度；鼓励贫困户自主创业为其优先提供贷款支持．党和人民的共同努力，扶贫工作取得了很大进展，如图 2，2013 年至 2016 年，我国现行标准下的农村贫困人口由 8249 万人减少至 4335 万人，2018 年底，全国贫困人口减至 1660 万人，贫困发生率从 2013 年的 10.2% 降至 1.7%．
（1）补全扇形统计图和条形统计图；
（2）贫困发生率指的是低于贫困线的人口占该地区全部人口的比例（贫困发生率 = 贫困人数 ÷ 统计全人数 ×100%）．贫困发生率是否低于 3%，是判断一个地区是否脱贫的一项重要指标．我国从 年开始达到了这个标准；
（3）结合 2013 年底的抽样调查结果，下列推断合理的是： ．
①生病是导致贫困的最主要原因，因此需要进一步完善医疗保险制度；
②全省约有 1800 人因贫穷面临辍学；
③通过各地捐款，可以有效缓解了生产资金短缺的困难；
④约有将近五分之一的贫困人口缺少劳动力和技术支持，我们可以通过实用技术培训，使有劳动能力的贫困人口和有意愿的残疾贫困人口掌握一技之长．

25. 如图，P 是 △ABC 外部的一定点，D 是线段 BC 上一动点，连接 PD 交 AC 于点 E．
小明根据学习函数的经验，对线段 PD，PE，CD 的长度之间的关系进行了探究．
下面是小明的探究过程，请补充完整．
（1）对于点 D 在 BC 上的不同位置，画图、测量，得到了线段 PD，PE，CD 的长度的几组值，如下表：
位置 1位置 2位置 3位置 4位置 5位置 6位置 7位置 8位置
在 PD，PE，CD 的长度这三个量中，确定 的长度是自变量， 的长度和 的长度都是这个自变量的函数；
（2）在同一平面直角坐标系 xOy 中，画出（1）中所确定的两个函数的图象；
（3）结合函数图象，解决问题：连接 CP，当 △PCD 为等腰三角形时，CD 的长度约为 cm（精确到 0.1）．

26. 在平面直角坐标系 xOy 中，二次函数 y=x2−2mx+1 图象与 y 轴的交点为 A，将点 A 向右平移 4 个单位长度得到点 B．
（1）直接写出点 A 与点 B 的坐标；
（2）求出抛物线的对称轴（用含 m 的式子表示）；
（3）若函数 y=x2−2mx+1 的图象与线段 AB 恰有一个公共点，求 m 的取值范围．

27. 在 △ABC 中，AB=BC，∠ABC=90∘，将线段 AB 绕点 A 逆时针旋转 α0∘<α<90∘ 得到线段 AD．作射线 BD，点 C 关于射线 BD 的对称点为点 E．连接 AE，CE．
（1）依题意补全图形；
（2）若 α=20∘，直接写出 ∠AEC 的度数；
（3）写出一个 α 的值，使 AE=2 时，线段 CE 的长为 3−1，并证明．

28. 在 △ABM 中，∠ABM=90∘，以 AB 为一边向 △ABM 的异侧作正方形 ABCD，以 A 为圆心，AM 为半径作 ⊙A，我们称正方形 ABCD 为 ⊙A 的“关于 △ABM 的友好正方形”，如果正方形 ABCD 恰好落在 ⊙A 的内部（或圆上），我们称正方形 ABCD 为 ⊙A 的“关于 △ABM 的绝对友好正方形”，
例如，图 1 中正方形 ABCD 是 ⊙A 的“关于 △ABM 的友好正方形”．
（1）如图 2，在 △ABM 中，BA=BM，∠ABM=90∘，在图中画出 ⊙A 的“关于 △ABM 的友好正方形 ABCD”；
（2）若点 A 在反比例函数 y=kx（k>0，x>0）上，它的横坐标是 2，过点 A 作 AB⊥y 轴于 B，若正方形 ABCD 为 ⊙A 的“关于 △ABO 的绝对友好正方形”求 k 的取值范围；
（3）若点 A 是直线 y=−x+2 上的一个动点，过点 A 作 AB⊥y 轴于 B，若正方形 ABCD 为 ⊙A 的“关于 △ABO 的绝对友好正方形”，求出点 A 的横坐标 m 的取值范围．
答案
第一部分
1. B
2. C
3. A
4. B
5. D
6. A
7. C
8. D
第二部分
9. 2a−12
10. 圆柱
11. x≠1
12. −1≤y≤3
13. 答案不唯一，如 a=0，b=−1
14. 54
15. x−6+x−3+x+x+3+x+6=60 或 5x=60
16. ②③
第三部分
17. 原式=3×33−1+2+2−3=3.
18.
4x−1x. ⋯⋯②
由 ① 得
4x−4由 ② 得
3x+1>2x.x>−1.
所以
−119. ∵OG 平分 ∠MON，
∴∠MOG=∠NOG，
∵AB⊥OG 于点 B，
∴∠ABO=90∘，
∵C 为线段 OA 中点，
∴BC=12AO=CO，
∴∠MOG=∠CBO，
∴∠NOG=∠CBO，
∴BC∥ON．
20. （1） Δ=−2k2−4k2+k−2=−4k+8，
∵ 有两个不相等的实数根，
∴−4k+8>0，
∴k<2．
（2） ∵k<2 且 k 为正整数，
∴k=1，
∴x2−2x=0，
解得 x1=0，x2=2．
21. （1） ∵BF∥AC，CF∥BD，
∴ 四边形 OBFC 是平行四边形．
∵ 矩形 ABCD，
∴AC=BD，BO=12BD，CO=12AC．
∴OB=OC．
∴ 四边形 OBFC 是菱形．
（2） 连接 FO 并延长交 AD 于 H，交 BC 于 K．
∵ 菱形 OBFC，
∴∠BKO=90∘．
∵ 矩形 ABCD，
∴∠DAB=∠ABC=90∘，OA=OD．
∴ 四边形 ABKH 是矩形．
∴∠DHF=90∘，HK=AB=2．
∴H 是 AD 中点．
∵O 是 BD 中点，
∴OH=12AB=1．
∴FK=OK=OH=1．
∴HF=3．
∵tan∠AFD=23，
∴HD=AH=2．
∴BC=AD=4．
由勾股定理：AC=AB2+BC2=25．
22. （1） 依题意补全图形．
证明：
∵ 等边 △ABC，
∴AB=AC，
∴AB=AC，
∵AD 过圆心 O，
由垂径定理，∠AEC=90∘，
∵DF∥BC，
∴∠ADF=90∘，
∴DF 与 ⊙O 相切．
（2） 连接 DC，
∵ 等边 △ABC，
∴AB=AC=BC=6，∠BAC=60∘，
∵AD⊥BC，
∴∠DAC=30∘，
∵AD 是直径，
∴∠ACD=90∘，
∴DC=23，
∵∠DCF=90∘，∠F=60∘，
∴CF=2．
23. （1） A3,2，k=6．
（2） ① 3；
② 424. （1） 扇形统计图补充完整 47.1%；
条形统计图补充完整 4335．
（2） 2018
（3） ①④
25. （1） CD；PD；PE
（2）
（3） 2.6，1.9，3.5
26. （1） A0,1，B4,1．
（2） x=−b2a=m．
（3） m≤0 或 m>2．
27. （1） 补全图形．
（2） 135∘．
（3） a=30∘．
证明：过 A 作 AG⊥CE 于 G，连接 AC．
由题意，BC=BE=BA，
∴∠BCE=∠2，∠BAE=∠1，
∵∠BCE+∠2+∠BAE+∠1+∠ABC=360∘，
∵∠ABC=90∘，
∴2∠2+∠1=270∘，
∴∠2+∠1=135∘，
∴∠AEG=45∘，
∵AE=2，
∴AG=GE=1，
当 α=30∘ 时，
∴∠EBC=30∘，
∵BC=BE，
∴∠BCG=75∘，
∵∠BCA=45∘，
∴∠ACG=30∘，
∴CG=3，
∴CE=3−1．
28. （1） 补全图形．
（2） 设 A2,a，
当 a=2 时，正方形 ABCD 的顶点 C 恰好落在 ⊙A 上；
当 a>2 时，正方形 ABCD 的顶点均落在 ⊙A 内部；
当 a<2 时，正方形 ABCD 的顶点 C 落在 ⊙A 外部；
∵ 反比例函数 y=kx（k>0，x>0）过点 A2,a，
∴ 当 a≥2 时，k≥4．
（3） 当 m=1 时，正方形 ABCD 的顶点 C 恰好落在 ⊙A 上；
当 0当 m=0 时，△ABO 不存在；
当 m<0 时，正方形 ABCD 均落在 ⊙A 内部；
当 m>1 时，正方形 ABCD 的顶点 C 落在 ⊙A 外部（当 m=2 时 △ABO 不存在）；
所以，0