2021年上海市嘉定区中考一模数学试卷（期末）

这是一份2021年上海市嘉定区中考一模数学试卷（期末），共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共6小题；共30分）
1. 如果实数 a，b，c，d 满足 ab=cd，下列四个选项中，正确的是
A. a+bb=c+ddB. aa+b=cc+dC. a+cb+d=cdD. a2b=c2d

2. 在平面直角坐标系 xOy 中，已知点 P1,3，点 P 与原点 O 的连线与 x 轴的正半轴的夹角为 α（0∘<α<90∘），那么 tanα 的值是
A. 1010B. 13C. 31010D. 3

3. 抛物线 y=2x2−3 的顶点坐标是
A. 2,−3B. 2,3C. 0,−3D. 0,3

4. 已知单位向量 e 与非零向量 a，b，下列四个选项中，正确的是
A. ∣a∣e=aB. ∣e∣b=bC. 1∣a∣a=eD. 1∣a∣a=1∣b∣b

5. 在 Rt△ABC 中，∠ACB=90∘，∠A=30∘，CD⊥AB，垂足为 D．下列四个选项中，不正确的是
A. ACAB=32B. BCCD=32C. BDCD=33D. BCAC=33

6. 二次函数 y=ax+m2+k 的图象如图所示，下列四个选项中，正确的是
A. m<0，k<0B. m<0，k>0C. m>0，k<0D. m>0，k>0

二、填空题（共12小题；共60分）
7. 正方形的边长与它的对角线的长度的比值为 ．

8. 如果点 P 是线段 AB 的黄金分割点，且 AP>PB，那么 BPAP 的比值是 ．

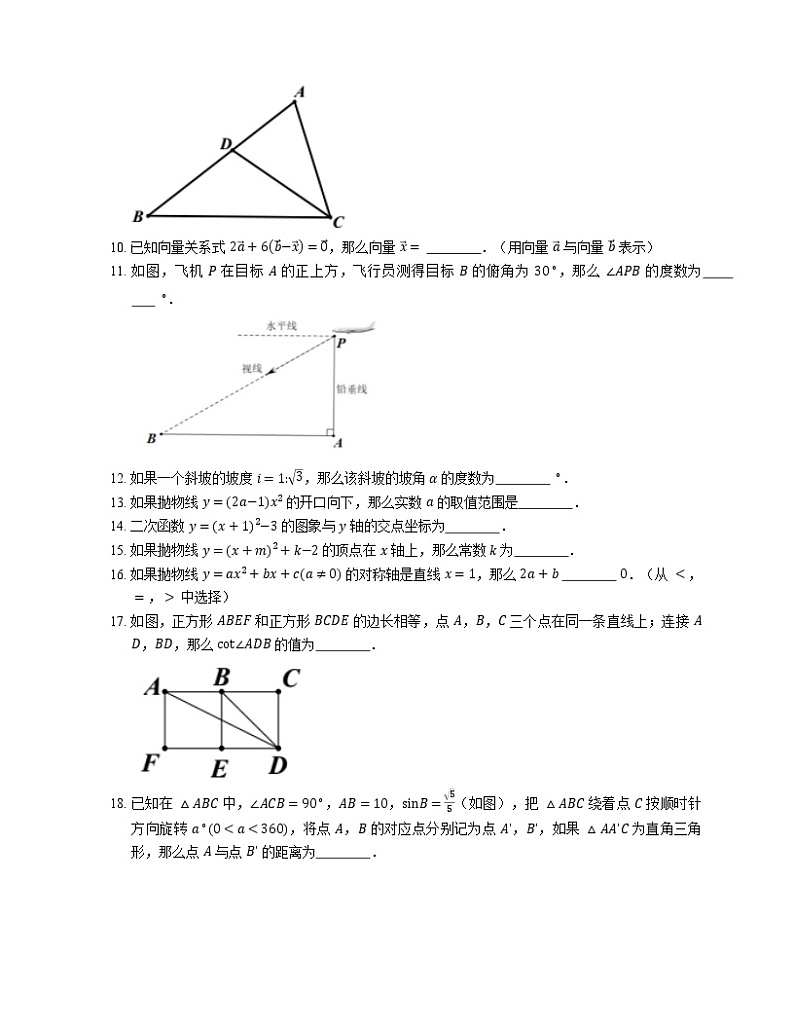
9. 如图，点 D 在 △ABC 的 AB 边上，当 ADAC= 时，△ACD 与 △ABC 相似．

10. 已知向量关系式 2a+6b−x=0，那么向量 x= ．（用向量 a 与向量 b 表示）

11. 如图，飞机 P 在目标 A 的正上方，飞行员测得目标 B 的俯角为 30∘，那么 ∠APB 的度数为 ∘．

12. 如果一个斜坡的坡度 i=1:3，那么该斜坡的坡角 α 的度数为 ∘．

13. 如果抛物线 y=2a−1x2 的开口向下，那么实数 a 的取值范围是 ．

14. 二次函数 y=x+12−3 的图象与 y 轴的交点坐标为 ．

15. 如果抛物线 y=x+m2+k−2 的顶点在 x 轴上，那么常数 k 为 ．

16. 如果抛物线 y=ax2+bx+ca≠0 的对称轴是直线 x=1，那么 2a+b 0．（从 <，=，> 中选择）

17. 如图，正方形 ABEF 和正方形 BCDE 的边长相等，点 A，B，C 三个点在同一条直线上；连接 AD，BD，那么 ct∠ADB 的值为 ．

18. 已知在 △ABC 中，∠ACB=90∘，AB=10，sinB=55（如图），把 △ABC 绕着点 C 按顺时针方向旋转 a∘0
三、解答题（共7小题；共91分）
19. 计算：2sin45∘+2sin60∘−tan60∘⋅tan45∘．

20. 我们已经知道二次函数 y=ax2+bx+ca≠0 的图象是一条抛物线．研究二次函数的图象与性质，我们主要关注抛物线的对称轴、抛物线的开口方向、抛物线的最高点（或最低点）的坐标、抛物线与坐标轴的交点坐标、抛物线的上升或下降情况（沿 x 轴的正方向看）．
已知一个二次函数 y=ax2+bx+ca≠0 的大致图象如图所示．
（1）你可以获得该二次函数的哪些信息?（写出四条信息即可）
（2）依据目前的信息，你可以求出这个二次函数的解析式吗?
如果可以，请求出这个二次函数的解析式；如果不可以，请补充一个条件，并求出这个二次函数的解析式．

21. 如图，已知 AC 与 BD 相交于点 O，连接 AB．
（1）如果 AD∥BC，S△AOD=4，S△BOC=9，求：S△ABO．
（2）分别将 △AOD，△AOB，△BOC 的面积记为 S1，S2，S3，如果 S2 是 S1 与 S3 的比例中项，求证：AD∥BC．

22. 如图，在 △ABC 中，AB=AC=10，sinB=45．
（1）求边 BC 的长度；
（2）求 csA 的值．

23. 如图，已知矩形 DEFG 的边 DE 在 △ABC 的边 BC 上，顶点 G，F 分别在边 AB，AC 上．△ABC 的高 AH 交 GF 于点 I．
（1）求证：BD⋅EH=DH⋅CE；
（2）设 DE=n⋅EF（n 为正实数），求证：nBC+1AH=1EF．

24. 在平面直角坐标系 xOy 中（如图），已知点 A−1,2，点 B1,6，点 C1,4．如果抛物线 y=ax2+bx+3a≠0 恰好经过这三个点之中的两个点．
（1）试推断抛物线 y=ax2+bx+3 经过点 A，B，C 之中的哪两个点?简述理由；
（2）求常数 a 与 b 的值；
（3）将抛物线 y=ax2+bx+3 先沿与 y 轴平行的方向向下平移 2 个单位长度，再沿与 x 轴平行的方向，向右平移 tt>0 个单位长度，如果所得到的新抛物线经过点 C1,4．设这个新抛物线的顶点是 D，试探究 △ABD 的形状（写出简要的计算与推理过程）．

25. 在矩形 ABCD 中，AB=6，AD=8，点 E 在 CD 边上，tan∠DAE=12．点 F 是线段 AE 上一点，连接 BF，CF．
（1）如图 1，如果 tan∠CBF=34，求线段 AF 的长．
（2）如图 2，如果 CF=12BC，
①求证：∠CFE=∠DAE；
②求线段 EF 的长．
答案
第一部分
1. A
2. D
3. C
4. B
5. B
6. A
第二部分
7. 22
8. 5−12
9. ACAB
10. x=13a+b
11. 60；
12. 30
13. a<12
14. 0,−2
15. 2
16. =
17. 3
18. 25 或 65．
第三部分
19. 2sin45∘+2sin60∘−tan60∘⋅tan45∘=2×22+2×32−3×1=2+3−3=2.
20. （1） ①抛物线的开口向下（或者 a<0 ），②抛物线的顶点坐标为 2,7，③抛物线的对称轴为直线 x=2，④沿 x 轴的正方向看：直线 x=2 的左侧，图象是上升的（或 y 的值随着 x 的值的增大而增大）；在直线 x=2 的右侧，图象是下降的（或 y 的值随着 x 的值的增大而减小），⑤ b>0，⑥ c>0，⑦ a+b+c>0，⑧ a−b+c>0，⑨ 4a+b=0 等信息．
（2） 补充条件：C0,3，
由题意得，该抛物线的顶点坐标为 D2,7，
故而可设该抛物线的表达式为 y=ax−22+7
因为 C0,3 在该抛物线上，所以 3=a0−22+7，
解得 a=−1
故所求的二次函数的解析式为 y=−x−22+7 或 y=−x2+4x+3．
21. （1） ∵AD∥BC，
∴△AOD∽△COB．
∴S△AODS△COB=ODOB2．
又 ∵SAOD=4，S△BOC=9，
∴49=ODOB2．
∴ODOB=23．（负值已舍）
设点 A 到直线 BD 的距离为 h，易得 S△AOD=12OD⋅h，S△AOB=12OB⋅h，
∴S△AODS△AOB=ODOB．
将 ODOB=23，S△AOD=4 代入，得 4S△AOB=23，解得 S△AOB=6．
（2） 设点 A 到直线 BD 的距离为 h，易得 S△AOD=12OD⋅h，S△AOB=12OB⋅h，
∴S1S2=ODOB．
同理，S2S3=OAOC，
又 ∵S2 是 S1 与 S3 的比例中项，
∴S1S2=S2S3．
∴ODOB=OAOC．
∴AD∥BC．
22. （1） 过点 A 作 AD⊥BC，垂足为 D（如图所示），
在 △ABC 中，
∵AB=AC，AD⊥BC，
∴BD=CD=12BC．
在 Rt△ABD 中，
∵∠ADB=90∘，AB=10，sinB=45，
∴∴AD=AB⋅sinB=10×45=8．
∴BD=AB2−AD2=102−82=6．
∴BC=2BD=12．
（2） ∴cs∠BAC=AHAC=145÷10=725．
23. （1） ∵ 四边形 DEFG 是矩形，∴∠EDG=90∘．又 ∵∠AHC=90∘ ，
∴∠AHC=∠EDG．∴GD∥AH．
∴BDDH=BGAG．
同理可得 EF∥AH，CEEH=CFAF．
∵ 矩形 DEFG 的边 DE 在 △ABC 的边 BC 上，∴GF∥BC .
∴BGAG=CFAF．
∴BDDH=CEEH，即 BD⋅EH=DH⋅CE．
（2） 在 △ABC 中，∵GF∥BC，∴GFBC=AFAC, ⋯⋯①
在 △ACH 中，∵EF∥AH，∴EFAH=FCAC, ⋯⋯②
① + ②，GFBC+EFAH=AFAC+FCAC．
又 ∵AFAC+FCAC=AF+FCAC=ACAC=1，∴GFBC+EFAH=1．
∵GF=DE=n⋅EF，∴n⋅EFBC+EFAH=1．
∴nBC+1AH=1EF．
24. （1） 抛物线 y=ax2+bx+3 经过点 A 与点 B．
理由如下：
∵ 点 B1,6 与点 C1,4 的横坐标相同、纵坐标不同，
∴ 点 B 与点 C 不可能同时出现在函数 y=ax2+bx+3 的图象上．
∵ 当 x=0 时，y=ax2+bx+3=3，
∴ 点 0,3 在抛物线 y=ax2+bx+3 上．
设经过点 M0,3 与点 A−1,2 的直线表达式为 y=kx+b，
将 A−1,2，M0,3 代入 y=kx+b，
易得 b=3，k=1，进而得到 y=x+3．
∵ 当 x=1 时，y=x+3=4，
∴ 点 C1,4 在直线 y=x+3 上．
∴ 点 A−1,2，M0,3，C1,4 不可能同时出现在函数 y=ax2+bx+3 的图象上．
（2） 由抛物线 y=ax2+bx+3 经过点 A−1,2 与点 B1,6，
易得 a−b+3=2,a+b+3=6,
解这个方程组，得 a=1,b=2.
（3） 由第（2）小题可知，抛物线的表达式为 y=x2+2x+3．
即 y=x+12+2，顶点坐标为 −1,2．
将该抛物线向下平移 2 个单位长度，再向右平移 t 个单位长度，所得表达式为 y=x+1−t2．
∵ 点 C1,4 在抛物线 y=x+1−t2 上，
∴4=1+1−t2．
解得 t1=0（不合题意，舍去），t2=4．
得 y=x−32，
∴ 顶点 D 的坐标为 3,0．
易得 AD=25，AB=25，BD=210，AD2+AB2=BD2，
由 AD2+AB2=BD2 可得 ∠BAD=90∘，△ABD 是直角三角形；
由 AD=25=AB，可得 △ABD 是等腰三角形．
综上，△ABD 是等腰直角三角形．
25. （1） 过点 F 作 FH⊥AB，垂足为 H．
得 FH∥BC∥AD，∠BFH=∠CBF，∠AFH=∠DAE．
∵tan∠EAD=12，tan∠CBF=34，
∴tan∠AFH=12，tan∠BFH=34．
在 Rt△BFH 中，设 BH=3k，由 tan∠BFH=34 易得 FH=4k．
在 Rt△AFH 中，由 FH=4k，tan∠AFH=12 易得 AH=2k，AF=5k．
又 ∵AB=6，
∴2k+3k=6，解得 k=65．
∴AH=125，AF=1255．
（2） ①如图 2，延长 AE 交 BC 的延长线于 G．
易得 AD∥BG，∠DAE=∠G，ADCG=DECE，
在 Rt△ADE 中，
∵∠D=90∘，tan∠EAD=12，AD=8，
∴DE=AD⋅tan∠EAD=4，CE=CD−DE=6−4=2．
∴8CG=42．解得 CG=4．
又 ∵CF=12BC=4，
∴CG=CF，
∴∠CFG=∠G．
∴∠CFE=∠DAE．
②如图 3，连接 BD 交 AE 于 P，类似（1）可求 AP=1255．
∵AB∥CD，
∴DPBP=ABDE．
将 AB=6，DE=4 代入，得 DPBP=32．
又 ∵BD=10，
∴DP=DE=4．
∴∠DPE=∠DEP．
又 ∵∠APD=180∘−∠DPE，∠CEF=180∘−∠DEP，
∴∠APD=∠CEF．
又 ∵∠CFE=∠DAE，
∴△CEF∽△APD．
∴APEF=DPCE．
将 AP=1255，DP=4，CE=CD−DE=2 代入，得 EF=655．