2020-2021学年3.1.1 一元一次方程教学设计及反思

这是一份2020-2021学年3.1.1 一元一次方程教学设计及反思，共8页。教案主要包含了复习回顾，典型例题，课堂小结，思考等内容，欢迎下载使用。
课题
小结复习
教科书
书名：数学七年级上册
出版社：人民教育出版社 出版日期： 年 月
教学目标
教学目标：1. 复习一元一次方程全章的知识结构、复习一元一次方程的相关概念、等式的性质、一元一次方程的解法；
2.在复习的过程中，体会解方程的目标和化归思想；
3.通过知识结构图体会数学问题从产生到解决的过程以及数学知识体系建立的过程，增强数学应用的意识，提高学习数学的热情。
教学重点、难点：复习全章知识结构，体会化归数学思想。
教学过程
时间
教学环节
主要师生活动
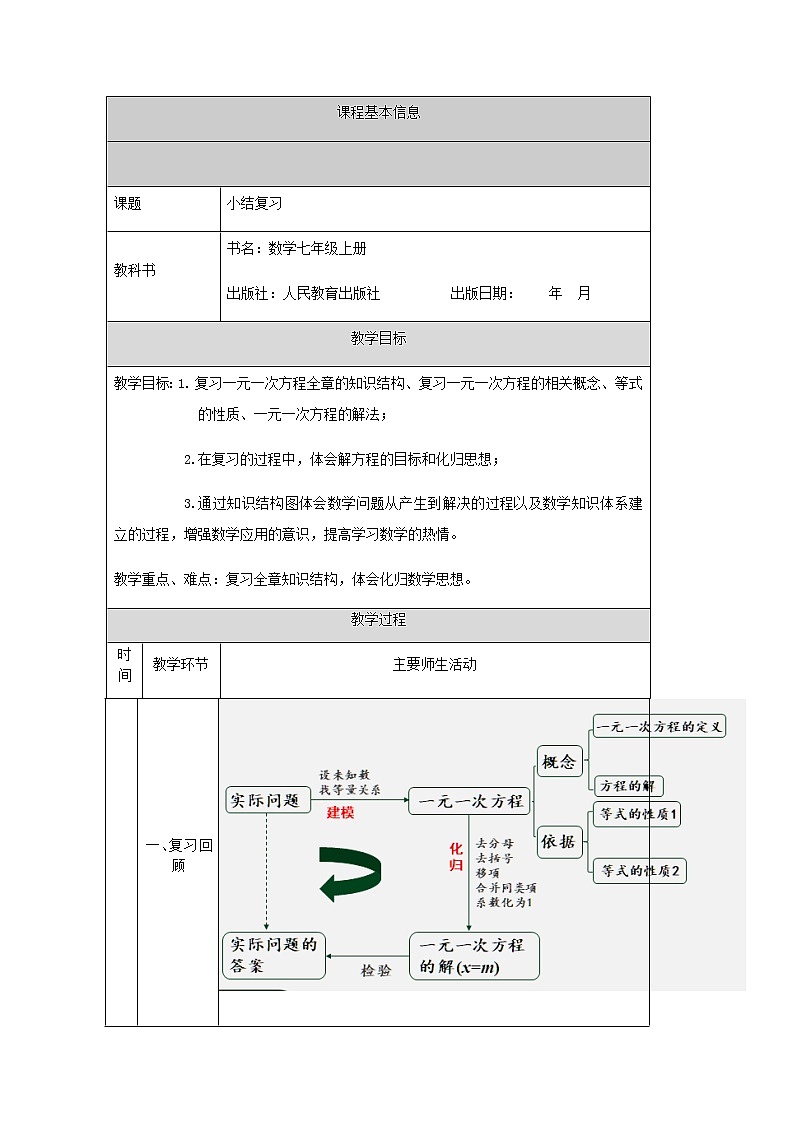
一、复习回顾
结合本章知识结构图复习本章的学习过程。
本节课主要复习一元一次方程的有关概念和解方程这两部分内容。
1. 一元一次方程只含有一个未知数，未知数的次数都是1，等号两边都是整式的方程叫做一元一次方程.
例如 方程 ；
2. 方程的解使方程中等号左右两边相等的未知数的值叫做这个方程的解.
例如 方程 2x+1=x+2,
当x=1时，左边=2x+1=3，右边=x+2=3，
则x=1是方程2x+1=x+2的解.
当x=2时，左边=2x+1=5，右边=x+2=4，
则x=2不是方程2x+1=x+2的解.
3. 等式的性质
等式的性质1 等式的两边同时加（或减）同一个数（或式子）， 结果仍相等。 如果 a=b，那么a ± c=b± c.
例如 等式 x+4=7,两边同时减4得x =3.
等式的性质2为等式的两边乘同一个数，或除以同一个不为0的数，结果仍相等.
用字母形式表示为，如果 a=b，那么a c=bc. 如果 a=b（c≠0），那么
例如等式-2x=4, 两边同时除以-2得 ,所以 x=-2.
等式的性质2 等式的两边乘同一个数，或除以同一个不为0的数，结果仍相等.
如果 a=b，那么a c=bc. 如果 a=b（c≠0），那么 .
12分
二、典型例题
例1 若m-1xm-2=0是关于x的一元一次方程，求m的值
解：由题意可知|m|=1 ，所以 m=1或-1.
又因为m-1 ≠ 0 ，所以 m ≠1.所以 m =-1.
例2（1） x=1是方程(k-1)x+9=0的解，则k=
（2）若关于x的方程2x+5a=3的解与方程2x+2=0的解相同，则a的值是
解：（1）将x=1代入方程(k-1)x+9=0可得k-1+9=0，则k=-8
（2）方程的2x+2=0解为x=-1,将x=-1代入方程2x+5a=3,得到2× (-1)x+5a=3,则a=1.
例3 判断
（1）-x+12=3，根据等式的性质2，在等式两边同时乘2，可以得到-x+1=6。（×）
（2）x-32-x3=1+x+34，根据等式的性质2，在等式两边同时乘12，可以得到6x-3-4x=1+3x+3 . （×）
例4解方程
（1）1+x3=3x+12+1
解：
21+x=33x+1+6
2+2x=9x+3+6
2x-9x=3+6-2
-7x=7
x=-1
检验：
x=-1时，方程的左边为1+（-1）3=0，方程的右边为3×-1+12+1=0
方程的左边和右边相等，所以x=-1是原方程的解
（2）119x+27=29x-57
解法一：
77x+18=14x-45
77x-14x=-18-4
63x=-63
x=-1
解法二：
x=-1
（3）
解法一
2(3x+5)+5(10x+2)=30
6x+10+50x+10=30
56x=10
解法二：
3~4分
三、课堂小结
本节课，我们主要复习了一元一次方程的有关概念和解一元一次方程。
这里等式的性质是解方程中部分步骤的依据。如，去分母，移项、系数化1等。
另外，在解一元一次方程时，一般要先观察方程的特点，根据方程的特点，采取灵活、合理的解方程的步骤。解方程的目的是将所给方程向着x=a（常数）的形式转化，是一种化归的思想。
6分
四、思考
1. 解关于x的方程 其中a、b是有理数
解：3(3x+a)=6-2(2x-b)
9x+3a=6-4x+2b
9x+4x=6+2b-3a
13x=6+2b-3a
2. 当k取什么整数时，关于x的方程2kx-6=(k+2)x有整数解？
解：原方程可化为2kx-6=kx+2x，合并同类项得(k-2)x =6,
k-2≠0时，方程的解为
因为x为整数，
所以k-2为6的约数，即k-2 =±1,±2,±3,±6.
则k可以取-4 、-1 、0 、1 、 3、4、5、8.
2分
布置作业
教材111页：2、3、4