2020版高考数学（天津专用）大一轮精准复习课件：6.1　数列的概念及其表示 【KS5U 高考】

这是一份2020版高考数学（天津专用）大一轮精准复习课件：6.1　数列的概念及其表示 【KS5U 高考】，共14页。

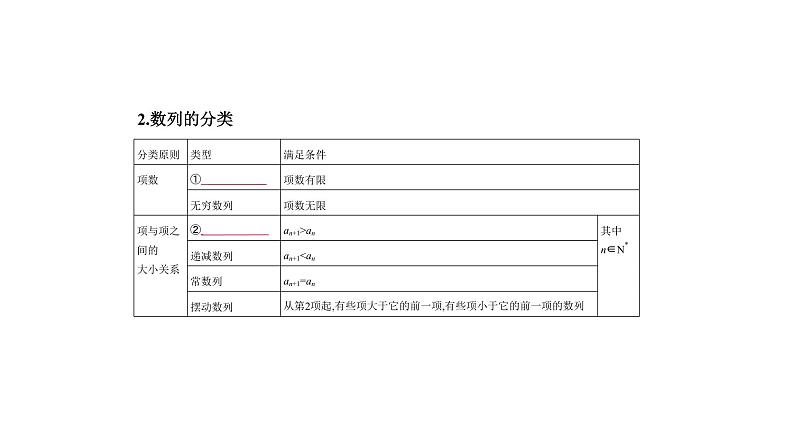
3.数列与函数的关系从函数观点看,数列可以看成以N*(或它的有限子集)为定义域的函数an= f(n),当自变量按照从小到大的顺序依次取值时,所对应的一列函数值.反 之,对于函数y=f(x),如果f(i)(i=1,2,3,…)有意义,那么我们可以得到一个数 列f(1),f(2),f(3),…,f(n),….4.通项公式如果数列{an}的第n项与序号n之间的关系可以用一个式子an=f(n)来表 示,那么这个式子叫做这个数列的③　通项公式    .
那么这个式子叫做数列{an}的④　递推公式    .6.数列的前n项和及其与通项的关系(1)Sn=a1+a2+…+an;(2)an= 
5.递推公式如果已知数列{an}的第一项(或前几项),且从第二项(或某一项)开始任 何一项an与它的前一项an-1(或前几项)间的关系可以用一个式子来表示,
考向一    求数列的通项公式
例1　若数列{an}满足a1+a2+a3+…+an=3n-2,那么这个数列的通项公式为  (　　)A.an=2×3n-1　    B.an=3× C.an=3n-2　    D.an= 
解析　∵数列{an}满足a1+a2+a3+…+an=3n-2①,∴当n=1时,a1=1;当n≥2时,a1+a2+a3+…+an-1=3n-1-2②,①-②得an=2×3n-1,∵2×31-1≠1=a1,故an= 故选D.
考向二    数列性质的应用
解析　∵数列{an}满足a1=1,an+1= (n∈N*),∴an>0, = +1,则 +1=2 .∴数列 是等比数列,且首项为 +1=2,公比为2.∴ +1=2n.∴bn+1=(n-2λ) =(n-2λ)·2n(n∈N*).∴bn=(n-1-2λ)·2n-1(n≥2).∵数列{bn}是单调递增数列,∴bn+1>bn.
∴(n-2λ)·2n>(n-1-2λ)·2n-1(n≥2).可得λ< (n≥2),∴λ< .又当n=1时,b2>b1,∴(1-2λ)·2>- λ.解得λ< .综上,λ的取值范围是λ< ,故选A.
方法1  利用an与Sn的关系求通项1.由Sn求an时,要分n=1和n>1两种情况讨论,然后验证两种情况可否用统 一的解析式表示,若不能,则用分段函数的形式表示为an=  2.利用an和Sn的关系,可以消去Sn得到关于an与an-1的关系,也可以消去an得 到Sn与Sn-1之间的关系,前者可直接求出an,后者可求出Sn,然后再利用Sn与 an的关系求an.
例1　已知数列{an}的前n项和Sn=3n(λ-n)-6,若数列{an}单调递减,则λ的取 值范围是 (　　)A.(-∞,2)　    B.(-∞,3)C.(-∞,4)　    D.(-∞,5)
解析　∵Sn=3n(λ-n)-6①,∴Sn-1=3n-1(λ-n+1)-6,n>1②,①-②,得an=3n-1(2λ-2n-1)(n>1,n∈N*),∵{an}为单调递减数列,∴an>an+1(n> 1,n∈N*),且a1>a2,∴3n-1(2λ-2n-1)>3n(2λ-2n-3),且31·(λ-1)-6>32-1·(2λ-4-1),化 为λ1,n∈N*),且λ<2,∴λ<2,∴λ的取值范围是(-∞,2).故选A.
方法2  利用递推关系求数列的通项1.形如an+1=an+f(n),常用累加法,即利用an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)(n ≥2,n∈N*)求解.2.形如an+1=an·f(n),常用累乘法,即利用an=a1· · ·…· (n≥2,n∈N*)求解.3.形如an+1=ban+d(b≠1),常用构造等比数列法.对an+1=ban+d变形得an+1+x=b(an+x) ,则{an+x}是公比为b的等比数列,利用它可求出an.4.形如an+1= ,将其变形为 = · + .
若p=r,则 是等差数列,且公差为 ,可用等差数列的通项公式求 ,进而求an;若p≠r,则采用3的方法来求 ,进而求an.5.形如an+2=pan+1+qan(p+q=1),常用构造等比数列法.将an+2=pan+1+qan变形为an+2-an+1=(-q)·(an+1-an),则{an-an-1}(n≥2,n∈N*)是等 比数列,且公比为-q,可以求得an-an-1=f(n)(n≥2,n∈N*),然后用累加法求an.