2020版高考数学(天津专用)大一轮精准复习精练:5.2 平面向量数量积与应用 Word版含解析【KS5U 高考】
展开5.2 平面向量数量积与应用
挖命题
【考情探究】
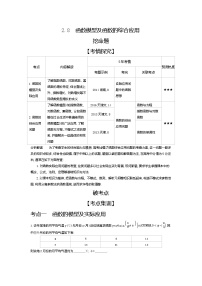
考点 | 内容解读 | 5年考情 | 预测热度 | ||
考题示例 | 考向 | 关联考点 | |||
1.平面向量的数量积 | 1.理解平面向量数量积的含义及其物理意义 2.了解平面向量的数量积与向量投影的关系 3.掌握数量积的坐标表达式,会进行平面向量数量积的运算 4.理解数量积的性质并能运用 | 2014天津,8 | 基底法线性表示向量 | 向量的共线表示 | ★★★ |
2.平面向量数量积的应用 | 1.能运用数量积解决两向量的夹角问题和长度问题 2.会用数量积判断两个向量的平行、垂直关系 3.会用向量方法解决某些简单的平面几何问题、力学问题以及一些实际问题 | 2015天津,14 | 向量方法解决平面几何问题 | 基本不等式 | ★★★ |
分析解读 在天津高考中,平面向量的数量积常以平面图形为载体,借助平行四边形法则和三角形法则来考查.当平面图形为特殊图形时,可以建立直角坐标系,通过坐标运算求数量积;遇到模的问题时,通常是进行平方,利用数量积的知识解决,主要从以下几个方面考查:1.理解数量积的定义、几何意义及其应用.2.掌握向量数量积的性质及运算律;掌握求向量长度的方法.3.会用向量数量积的运算求向量夹角,判断或证明向量垂直.4.利用数形结合的方法和函数的思想解决最值等综合问题.
破考点
【考点集训】
考点一 平面向量的数量积
1.已知A,B是单位圆O上的两点(O为圆心),∠AOB=120°,点C是线段AB上不与A、B重合的动点.MN是圆O的一条直径,则·的取值范围是( )
A. B.[-1,1) C. D.[-1,0)
答案 A
2.(2012北京,13,5分)已知正方形ABCD的边长为1,点E是AB边上的动点,则·的值为 ;·的最大值为 .
答案 1;1
考点二 平面向量数量积的应用
3.已知向量||=2,||=1,且|-2|=2,则向量和的夹角为( )
A.30° B.60° C.120° D.150°
答案 C
4.已知向量a=(cos θ,sin θ),向量b=(,-1),则|2a-b|的最大值,最小值分别是( )
A.4,0 B.4,4 C.4,0 D.16,0
答案 A
5.已知向量a是单位向量,向量b=(2,2),若a⊥(2a+b),则a,b的夹角为 .
答案
炼技法
【方法集训】
方法1 求平面向量的模的方法
1.已知平面向量,满足||=||=1,·=-,若||=1,则||的最大值为( )
A.-1 B.-1 C.+1 D.+1
答案 D
2.在△ABC中,∠BAC=60°,AB=5,AC=4,D是AB上一点,且·=5,则||等于( )
A.6 B.4 C.2 D.1
答案 C
3.已知向量a与向量b的夹角为,且|a|=|b|=2,若向量c=xa+yb(x∈R且x≠0,y∈R),则的最大值为( )
A. B. C. D.3
答案 A
方法2 求平面向量的夹角的方法
4.△ABC是边长为2的等边三角形,向量a,b满足=2a,=2a+b,则向量a,b的夹角为( )
A.30° B.60° C.120° D.150°
答案 C
5.若e1,e2是平面内夹角为60°的两个单位向量,则向量a=2e1+e2,b=-3e1+2e2的夹角为( )
A.30° B.60° C.90° D.120°
答案 D
6.已知|a|=,a·b=-,且(a-b)·(a+b)=-15,则向量a与b的夹角θ为( )
A. B. C. D.
答案 C
方法3 用向量法解决平面几何问题的方法
7.(2015湖南,9,5分)已知点A,B,C在圆x2+y2=1上运动,且AB⊥BC.若点P的坐标为(2,0),则|++|的最大值为( )
A.6 B.7 C.8 D.9
答案 B
8.已知向量,的夹角为60°,||=||=2,若=2+,则△ABC为( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形
答案 C
过专题
【五年高考】
A组 自主命题·天津卷题组
考点一 平面向量的数量积
1.(2016天津,7,5分)已知△ABC是边长为1的等边三角形,点D,E分别是边AB,BC的中点,连接DE并延长到点F,使得DE=2EF,则·的值为( )
A.- B. C. D.
答案 B
2.(2014天津,8,5分)已知菱形ABCD的边长为2,∠BAD=120°,点E,F分别在边BC,DC上,BE=λBC,DF=μDC.若·=1,·=-,则λ+μ=( )
A. B. C. D.
答案 C
考点二 平面向量数量积的应用
(2015天津,14,5分)在等腰梯形ABCD中,已知AB∥DC,AB=2,BC=1,∠ABC=60°.动点E和F分别在线段BC和DC上,且=λ,=,则·的最小值为 .
答案
B组 统一命题、省(区、市)卷题组
考点一 平面向量的数量积
1.(2018课标Ⅱ,4,5分)已知向量a,b满足|a|=1,a·b=-1,则a·(2a-b)=( )
A.4 B.3 C.2 D.0
答案 B
2.(2014课标Ⅱ,3,5分)设向量a,b满足|a+b|=,|a-b|=,则a·b=( )
A.1 B.2 C.3 D.5
答案 A
3.(2017课标Ⅰ,13,5分)已知向量a,b的夹角为60°,|a|=2,|b|=1,则|a+2b|= .
答案 2
4.(2016课标Ⅰ,13,5分)设向量a=(m,1),b=(1,2),且|a+b|2=|a|2+|b|2,则m= .
答案 -2
5.(2015湖北,11,5分)已知向量⊥,||=3,则·= .
答案 9
考点二 平面向量数量积的应用
1.(2018浙江,9,4分)已知a,b,e是平面向量,e是单位向量.若非零向量a与e的夹角为,向量b满足b2-4e·b+3=0,则|a-b|的最小值是( )
A.-1 B.+1 C.2 D.2-
答案 A
2.(2017课标Ⅱ,12,5分)已知△ABC是边长为2的等边三角形,P为平面ABC内一点,则·(+)的最小值是( )
A.-2 B.- C.- D.-1
答案 B
3.(2016课标Ⅲ,3,5分)已知向量=,=,则∠ABC=( )
A.30° B.45° C.60° D.120°
答案 A
4.(2016山东,8,5分)已知非零向量m,n满足4|m|=3|n|,cos<m,n>=.若n⊥(tm+n),则实数t的值为( )
A.4 B.-4 C. D.-
答案 B
5.(2014江西,14,5分)已知单位向量e1与e2的夹角为α,且cos α=,向量a=3e1-2e2与b=3e1-e2的夹角为β,则cos β= .
答案
C组 教师专用题组
1.(2015广东,9,5分)在平面直角坐标系xOy中,已知四边形ABCD是平行四边形,=(1,-2),=(2,1),则·=( )
A.5 B.4 C.3 D.2
答案 A
2.(2015福建,7,5分)设a=(1,2),b=(1,1),c=a+kb.若b⊥c,则实数k的值等于( )
A.- B.- C. D.
答案 A
3.(2014湖南,10,5分)在平面直角坐标系中,O为原点,A(-1,0),B(0,),C(3,0),动点D满足||=1,则|++|的取值范围是( )
A.[4,6] B.[-1,+1] C.[2,2] D.[-1,+1]
答案 D
4.(2018上海,8,5分)在平面直角坐标系中,已知点A(-1,0)、B(2,0),E、F是y轴上的两个动点,且||=2,则·的最小值为 .
答案 -3
5.(2015安徽文,15,5分)△ABC是边长为2的等边三角形,已知向量a,b满足=2a,=2a+b,则下列结论中正确的是 .(写出所有正确结论的编号)
①a为单位向量; ②b为单位向量; ③a⊥b;
④b∥; ⑤(4a+b)⊥.
答案 ①④⑤
6.(2014江苏,12,5分)如图,在平行四边形ABCD中,已知AB=8,AD=5,=3,·=2,则·的值是 .
答案 22
7.(2014重庆,12,5分)已知向量a与b的夹角为60°,且a=(-2,-6),|b|=,则a·b= .
答案 10
8.(2013课标Ⅰ,13,5分)已知两个单位向量a,b的夹角为60°,c=ta+(1-t)b.若b·c=0,则t= .
答案 2
9.(2013课标Ⅱ,13,5分)已知正方形ABCD的边长为2,E为CD的中点,则·= .
答案 2
解析 解法一:·=·(-)=-=22-×22=2.
解法二:以A为原点建立平面直角坐标系(如图),可得A(0,0),E(1,2),B(2,0),C(2,2),D(0,2),则=(1,2),=(-2,2),则·=(1,2)·(-2,2)=1×(-2)+2×2=2.
【三年模拟】
一、选择题(每小题5分,共40分)
1.(2018天津芦台一中模拟,7)在直角梯形ABCD中,AB∥CD,AB⊥AD,AB=2,CD=1,P为线段BC上的一点,设=,若·=,则||=( )
A.2 B. C. D.1
答案 A
2.(2018天津南开二模,8)设△ABC是边长为1的正三角形,M是△ABC所在平面上的一点,且+2λ+=,则当·取得最小值时,λ的值为( )
A. B. C.2 D.3
答案 A
3.(2019届天津新华中学期中,5)若非零向量a,b满足|a|=|b|,且(a-b)⊥(3a+2b),则a与b的夹角为( )
A. B. C.π D.π
答案 A
4.(2017天津南开一模,7)在△ABC中,AB=AC=1,=,=,·=-,则∠ABC=( )
A. B. C. D.
答案 C
5.(2017天津五校联考一模,7)在△ABC中,AC=2AB=2,∠BAC=120°,O是BC的中点,M是AO上的一点,且=3,则·的值是( )
A.- B.- C.- D.-
答案 A
6.(2019届天津南开中学第二次月考,7)在△ABC中,·=4,||=3,M,N分别是BC边上的三等分点,则·的值是( )
A.5 B. C.6 D.8
答案 C
7.(2017天津和平一模,7)如图,在平行四边形ABCD中,∠BAD=,AB=2,AD=1.若M、N分别是边AD、CD上的点,且满足==λ,其中λ∈[0,1],则·的取值范围是( )
A.[-3,1] B.[-3,-1] C.[-1,1] D.[1,3]
答案 B
8.(2018天津部分区县一模,7)已知点G是△ABC内的一点,且满足++=0,若∠BAC=,·=1,则||的最小值是( )
A. B. C. D.
答案 C
二、填空题(每小题5分,共45分)
9.(2018天津南开中学第三次月考,12)已知向量a与b的夹角为60°,若a=(0,2),|b|=1,则|a+2b|= .
答案 2
10.(2017天津南开三模,11)已知向量a,b满足|a|=,|b|=2,(a+b)⊥a,则向量a,b的夹角为 .
答案
11.(2017天津河西三模,12)已知等边△ABC的边长为2,平面内一点M满足=+,则·= .
答案 -2
12.(2017天津八校联考,13)如图,在矩形ABCD中,AB=,BC=2,点E为BC的中点,点F在边CD上,若·=,则·的值是 .
答案
13.(2018天津红桥二模,12)如图,在△ABC中,AD⊥AB,=,||=1,则·= .
答案
14.(2019届天津耀华中学第二次月考,13)已知向量、、满足=+,||=2,||=1,E、F分别是线段BC、CD的中点,若·=-,则向量与的夹角为 .
答案
15.(2018天津南开一模,13)在四边形ABCD中,AB=AC=AD=,AB⊥AD,则·的最小值为 .
答案 2-2
16.(2018天津十二区县一模,13)在等腰梯形中,AB∥CD,AB=2,AD=1,∠DAB=60°,若=3,=λ(λ∈R),且·=-1,则λ= .
答案
17.(2018天津北辰模拟,14)在梯形ABCD中,BC∥AD,∠BAD=60°,∠CDA=30°,AB=2,AD=6,CD=2,在边BC,DC上分别有动点E,F,使=λ,=μ,λ+μ=1,则·的最小值为 .
答案 6
2020版高考数学(天津专用)大一轮精准复习课件:2.8 函数模型及函数的综合应用 【KS5U 高考】: 这是一份2020版高考数学(天津专用)大一轮精准复习课件:2.8 函数模型及函数的综合应用 【KS5U 高考】,共12页。PPT课件主要包含了方法技巧等内容,欢迎下载使用。
2020版高考数学(天津专用)大一轮精准复习课件:6.4 数列的综合应用 【KS5U 高考】: 这是一份2020版高考数学(天津专用)大一轮精准复习课件:6.4 数列的综合应用 【KS5U 高考】,共16页。
2020版高考数学(天津专用)大一轮精准复习课件:5.2 平面向量数量积与应用 【KS5U 高考】: 这是一份2020版高考数学(天津专用)大一轮精准复习课件:5.2 平面向量数量积与应用 【KS5U 高考】,共16页。