2020版高考数学（天津专用）大一轮精准复习课件：9.7　圆锥曲线的综合问题【KS5U 高考】

展开

这是一份2020版高考数学（天津专用）大一轮精准复习课件：9.7　圆锥曲线的综合问题【KS5U 高考】，共18页。

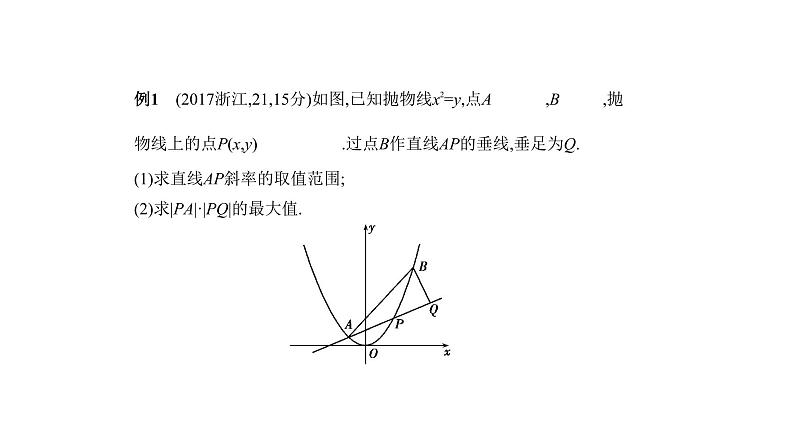
例1    (2017浙江,21,15分)如图,已知抛物线x2=y,点A ,B ,抛物线上的点P(x,y) .过点B作直线AP的垂线,垂足为Q.(1)求直线AP斜率的取值范围;(2)求|PA|·|PQ|的最大值.
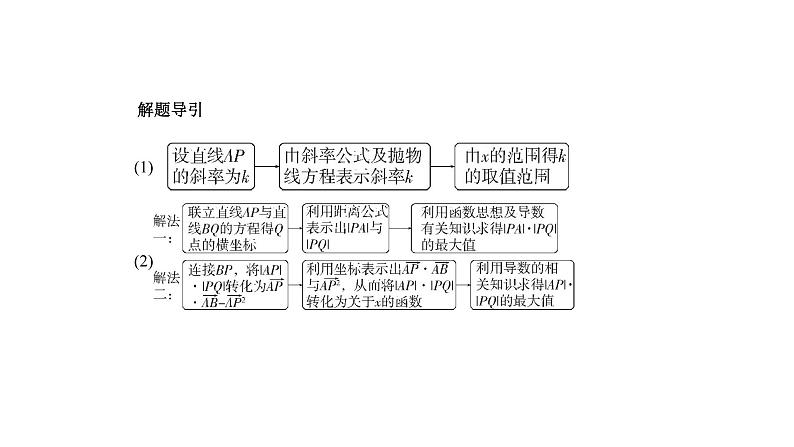
解析　(1)设直线AP的斜率为k,k= =x- ,因为- 所以|PA|·|PQ|=-(k-1)(k+1)3,令f(k)=-(k-1)(k+1)3.因为f '(k)=-(4k-2)(k+1)2,所以f(k)在区间上单调递增,在上单调递减,因此当k= 时,|PA|·|PQ|取得最大值 .解法二:如图,连接BP,|AP|·|PQ|=|AP|·|PB|·cs∠BPQ= · = ·( - )= · - .
易知P(x,x2) ,则 · =2x+1+2x2- =2x2+2x+ , = + =x2+x+ +x4- x2+ =x4+ x2+x+ .∴|AP|·|PQ|=-x4+ x2+x+ .
设f(x)=-x4+ x2+x+ ,则f '(x)=-4x3+3x+1=-(x-1)(2x+1)2,∴f(x)在上为增函数,在上为减函数,∴f(x)max=f(1)= .故|AP|·|PQ|的最大值为 .
方法2  圆锥曲线中的定值、定点问题的解题方法1.圆锥曲线中的定点、定值问题往往与圆锥曲线中的“常数”有关,如椭圆的长、短轴的长,双曲线的虚、实轴的长,抛物线的焦参数等,可通过直接计算求解,也可用“特殊位置法”和“相关曲线系数”求解.2.解决定点、定值问题常用的思想有两种:①从特殊入手,求含参变量的定点、定值,再证明这个定点、定值与变量无关;②直接推理计算,并在计算的过程中消去变量,从而得到定点、定值.
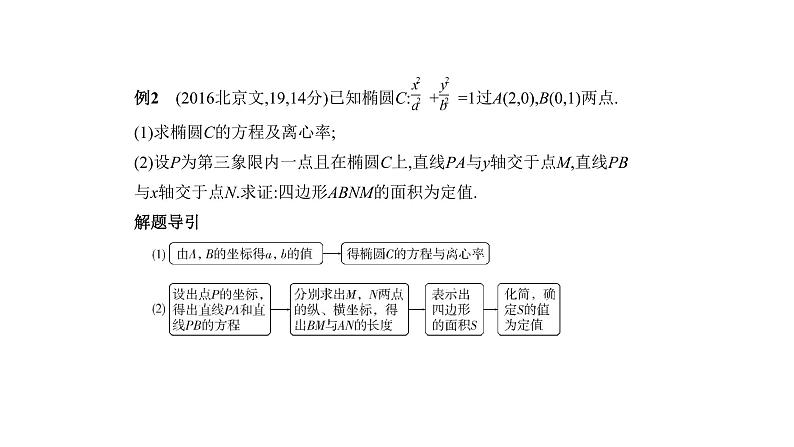
例2    (2016北京文,19,14分)已知椭圆C: + =1过A(2,0),B(0,1)两点.(1)求椭圆C的方程及离心率;(2)设P为第三象限内一点且在椭圆C上,直线PA与y轴交于点M,直线PB 与x轴交于点N.求证:四边形ABNM的面积为定值.解题导引
解析　(1)由题意得,a=2,b=1.所以椭圆C的方程为 +y2=1.又c= = ,所以离心率e= = .(2)证明:设P(x0,y0)(x0<0,y0<0),则 +4 =4.又A(2,0),B(0,1),所以,直线PA的方程为y= (x-2).令x=0,得yM=- ,从而|BM|=1-yM=1+ .直线PB的方程为y= x+1.
令y=0,得xN=- ,从而|AN|=2-xN=2+ .所以四边形ABNM的面积S= |AN|·|BM|= = = =2.从而四边形ABNM的面积为定值.
例3　已知椭圆C: +y2=1(a>0),过椭圆C的右顶点和上顶点的直线与圆x2+y2= 相切.(1)求椭圆C的方程;(2)设M是椭圆C的上顶点,过点M分别作直线MA,MB交椭圆C于A,B两点, 设这两条直线的斜率分别为k1,k2,且k1+k2=2,证明:直线AB过定点.解题导引
解析　(1)∵直线过点(a,0)和(0,1),∴直线的方程为x+ay-a=0,∵直线与圆x2+y2= 相切,∴ = ,解得a2=2,∴椭圆C的方程为 +y2=1.(2)证明:由题意得M(0,1).当直线AB的斜率不存在时,设A(x0,y0),则B(x0,-y 0),由k1+k2=2得 + =2,解得x0=-1.当直线AB的斜率存在时,设AB的方程为y=kx+m(m≠1),A(x1,y1),B(x2,y2),由 ⇒(1+2k2)x2+4kmx+2m2-2=0,得x1+x2= ,x1·x2= ,由k
1+k2=2⇒ + =2⇒ =2,即(2-2k)x1x2=(m-1)(x1+x2)⇒(2-2k)(2m2-2)=(m-1)(-4km),即(1-k)(m2-1)=-km (m-1),由m≠1,得(1-k)(m+1)=-km⇒k=m+1,所以y=kx+m=(m+1)x+m⇒m(x+1)=y-x,故直线AB过定点(-1,-1).综上,直线AB过定点(-1,-1).
方法3  存在性问题的解题策略1.此类问题一般分为探究条件、探究结论两种.若探究条件,则可先假设条件成立,再验证结论是否成立,成立则存在,否则不存在;若探究结论,则应先求出结论的表达式,再针对其表达式进行讨论,往往涉及对参数的讨论.2.反证法与验证法也是求解存在性问题的常用方法.
例4　如图,曲线C由上半椭圆C1: + =1(a>b>0,y≥0)和部分抛物线C2:y=-x2+1(y≤0)连接而成,C1与C2的公共点为A,B,其中C1的离心率为 .(1)求a,b的值;(2)过点B的直线l与C1,C2分别交于点P,Q(均异于点A,B),是否存在直线l, 使得以PQ为直径的圆恰好过点A?若存在,求出直线l的方程;若不存在, 请说明理由.
解析　(1)在C1,C2的方程中,令y=0,可得b=1,且A(-1,0),B(1,0)是上半椭圆C1的左、右顶点.由e= = 及a2-c2=b2=1可得a=2,∴a=2,b=1.(2)存在.由(1)知,上半椭圆C1的方程为 +x2=1(y≥0).由题易知,直线l与x轴不重合也不垂直,设其方程为y=k(x-1)(k≠0).代入C1的方程,整理得(k2+4)x2-2k2x+k2-4=0.(*)设点P的坐标为(xP,yP),∵直线l过点B,

相关课件更多