
初中苏科版第二章 轴对称图形2.5 等腰三角形的轴对称性背景图课件ppt
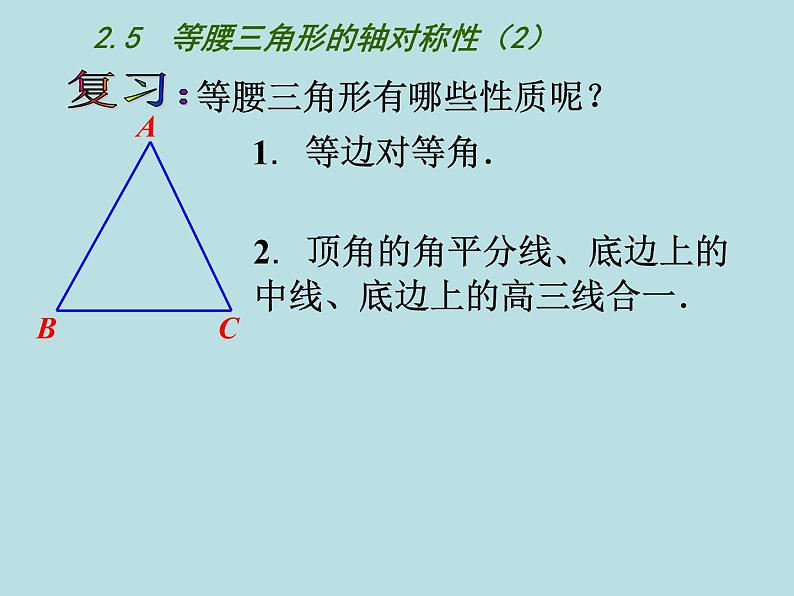
展开2.顶角的角平分线、底边上的中线、底边上的高三线合一.
2.5 等腰三角形的轴对称性(2)
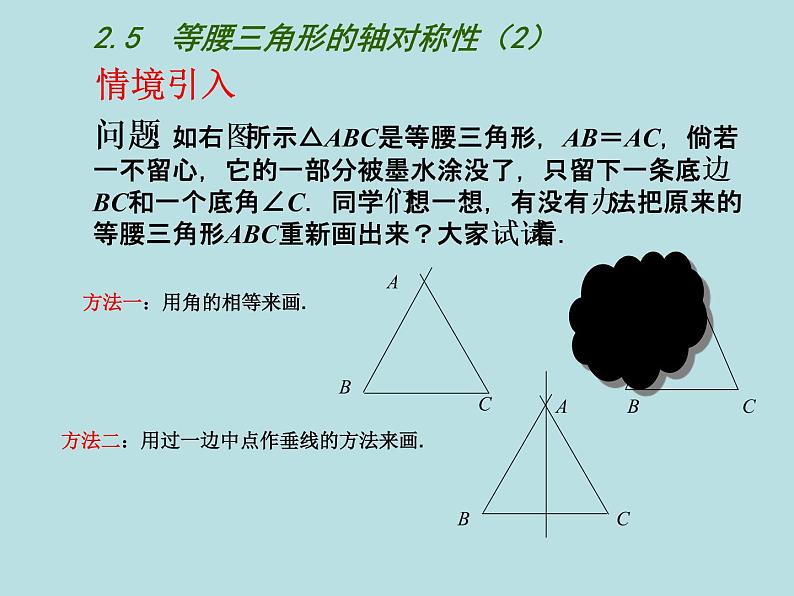
问题:如右图所示△ABC是等腰三角形,AB=AC,倘若一不留心,它的一部分被墨水涂没了,只留下一条底边BC和一个底角∠C.同学们想一想,有没有办法把原来的等腰三角形ABC重新画出来?大家试试看.
方法一:用角的相等来画.
方法二:用过一边中点作垂线的方法来画.
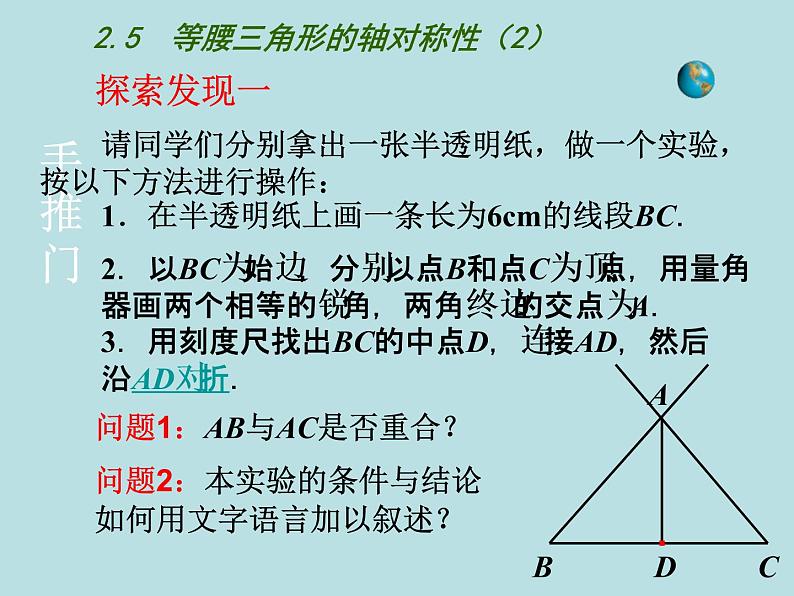
请同学们分别拿出一张半透明纸,做一个实验,按以下方法进行操作:
1.在半透明纸上画一条长为6cm的线段BC.
2.以BC为始边,分别以点B和点C为顶点,用量角器画两个相等的锐角,两角终边的交点为A.
3.用刻度尺找出BC的中点D,连接AD,然后沿AD对折.
问题1:AB与AC是否重合?
问题2:本实验的条件与结论如何用文字语言加以叙述?
在△BAT和△CAT中, ∠1=∠2(角平分线定义), ∠B=∠C(已知), AT=AT(公共边) , ∴△BAT≌△CAT(AAS),∴AB=AC(全等三角形对应边相等).
已知:在△ABC中,∠B=∠C 求证:AB=AC.
证明:(1)作∠A的平分线交BC于T.
(2)过A点作AD⊥BC,垂足为D.
∵AD⊥BC,∴∠ADB=∠ADC,在△ADB和△ADC中, ∠ADB=∠ADC, ∠B=∠C, AD=AD,∴△ADB≌△ADC,∴AB=AC.
思考:通过这题的证明你发现了什么结论?
如果一个三角形有两个角相等,那么这两个角所对的边也相等
( 简称“等角对等边”).
∵∠B=∠C∴AB=AC (等角对等边)
请思考: “等边对等角”与“等角对等边” 是否一样?它们的主要区别在哪里?
(它们的条件与结论正好调换了过来, 这也叫互逆命题).
思考3:一个三角形满足什么条件就是等边三角形?为什么?
思考1:什么是等边三角形?它与等腰三角形有什么区别与联系?
思考2:等边三角形的性质有哪些?请同学们说一说.
通过本节课的学习:(1)你有哪些收获?(2)你还有什么疑惑?
初中数学苏科版八年级上册2.5 等腰三角形的轴对称性课文配套ppt课件: 这是一份初中数学苏科版八年级上册<a href="/sx/tb_c17043_t3/?tag_id=26" target="_blank">2.5 等腰三角形的轴对称性课文配套ppt课件</a>,共15页。PPT课件主要包含了自主检测,自主展示,你还有其他发现吗,如何加以证明,符号语言,练一练,自主合作,巩固练习,例题讲解等内容,欢迎下载使用。
初中数学苏科版八年级上册2.5 等腰三角形的轴对称性优质课ppt课件: 这是一份初中数学苏科版八年级上册2.5 等腰三角形的轴对称性优质课ppt课件,共60页。PPT课件主要包含了5练习,数学活动等内容,欢迎下载使用。
2021学年2.5 等腰三角形的轴对称性评课课件ppt: 这是一份2021学年2.5 等腰三角形的轴对称性评课课件ppt,文件包含25等腰三角形的轴对称性1pptx、25等腰三角形的轴对称性2pptx、25等腰三角形的轴对称性3pptx、25等腰三角形的轴对称性2docx、25等腰三角形的轴对称性1docx、25等腰三角形的轴对称性3docx等6份课件配套教学资源,其中PPT共61页, 欢迎下载使用。