





高中人教B版 (2019)11.3.2 直线与平面平行教课课件ppt
展开直线与平面有几种位置关系?
其中平行是一种非常重要的关系,不仅应用较多,而且是学习平面和平面平行的基础.
有三种位置关系:在平面内,相交、平行.
反映直线和平面三种位置关系的依据是什么?公共点的个数没有公共点: 平行 仅有一个公共点:相交 无数个公共点:直线在平面内
这就是这节课我们要学的知识。——2.2.1直线与平面平行的判定
怎样判定直线与平面平行呢?
根据定义,判定直线与平面是否平行,只需判定直线与平面有没有公共点.但是,直线无限延长,平面无限延展,如何保证直线与平面没有公共点呢?
2.2.1直线与平面平行的判定
在生活中,注意到门扇的两边是平行的.当门扇绕着一边转动时,另一边始终与门框所在的平面没有公共点,此时门扇转动的一边与门框所在的平面给人以平行的印象.
将一本书平放在桌面上,翻动书的硬皮封面,封面边缘AB所在直线与桌面所在平面具有什么样的位置关系?
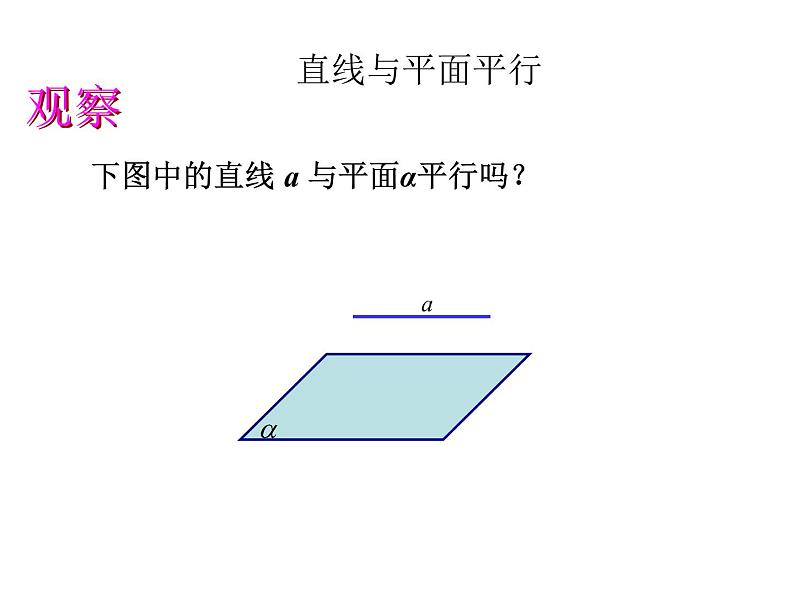
下图中的直线 a 与平面α平行吗?
(1)这两条直线共面吗?
平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.
证明直线与平面平行,三个条件必须具备,才能得到线面平行的结论.
直线与平面平行判定定理
(1)定义法:证明直线与平面无公共点;
(2)判定定理:证明平面外直线与平面内直线平行.
怎样判定直线与平面平行?
例1 求证:空间四边形相邻两边中点的连线平行于经过另外两边所在的平面.
已知:空间四边形ABCD中,E,F分别AB,AD的中点.
求证:EF//平面BCD.
因为 AE=EB,AF=FD,所以 EF//BD(三角形中位线的性质)
1.如图,长方体 中,
(1)与AB平行的平面是 ;
(2)与 平行的平面是 ;
(3)与AD平行的平面是 ;
例:两个全等的正方形ABCD和ABEF所在平面相交于AB,M∈AC,N∈BF,且AM=FN,求证:MN∥平面BCE.
高中数学人教B版 (2019)必修 第四册第十一章 立体几何初步11.3 空间中的平行关系11.3.2 直线与平面平行教学课件ppt: 这是一份高中数学人教B版 (2019)必修 第四册第十一章 立体几何初步11.3 空间中的平行关系11.3.2 直线与平面平行教学课件ppt,共16页。PPT课件主要包含了教学目标,重点难点,a∥α,练习2,主要利用中位线定理等内容,欢迎下载使用。
20.高一数学(人教B版)直线与平面平行的判定课件PPT: 这是一份20.高一数学(人教B版)直线与平面平行的判定课件PPT,共34页。
高中数学人教版新课标A必修22.1 空间点、直线、平面之间的位置关系教案配套ppt课件: 这是一份高中数学人教版新课标A必修22.1 空间点、直线、平面之间的位置关系教案配套ppt课件,共14页。PPT课件主要包含了线线平行线面平行,求证MN∥面SAD,SMMC=21,直线与平面平行的性质,线面平行的应用,线面平行线线平行,变式2,同理lb,高考题赏析等内容,欢迎下载使用。













