2020-2021学年17.1 勾股定理第2课时同步训练题

17.1 勾股定理

第2课时 勾股定理在求距离中应用

基础训练

知识点1 长度的计算

1.(2016·哈尔滨)如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在的位置B处与灯塔P之间的距离为(　　)

A.60海里    B.45海里

C.20海里 D.30海里

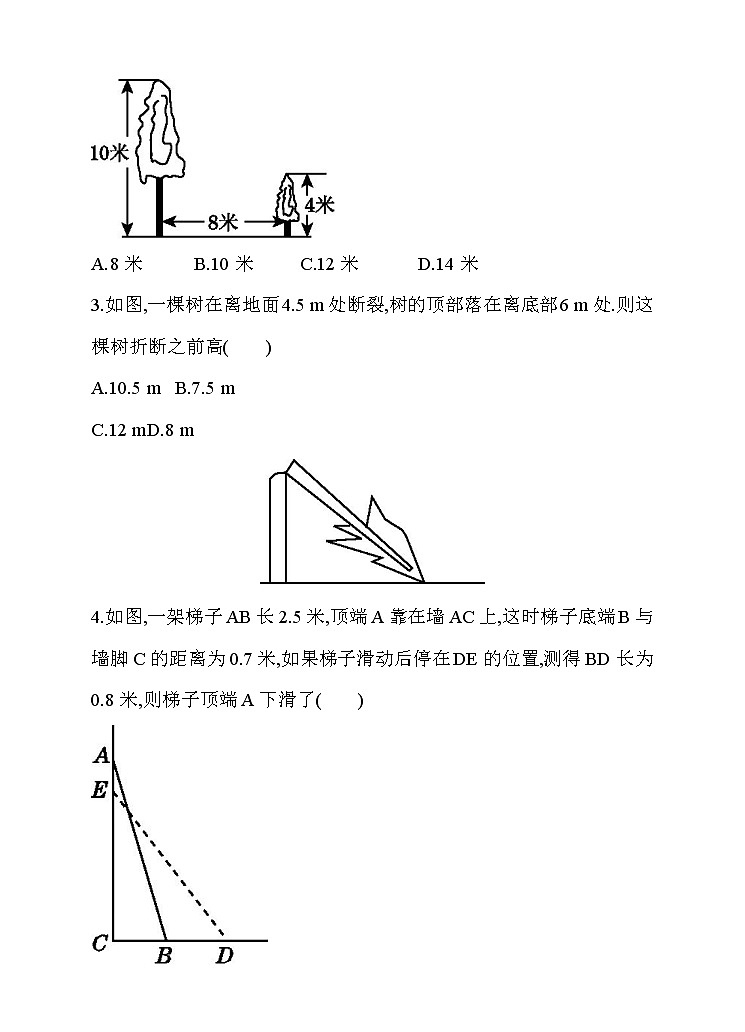
2.如图,有两棵树,一棵高10米,另一棵高4米,两树相距8米,一只小鸟从一棵树的树顶飞到另一棵树的树顶,小鸟至少飞行(　　)

A.8米      B.10米     C.12米      D.14米

3.如图,一棵树在离地面4.5 m处断裂,树的顶部落在离底部6 m处.则这棵树折断之前高(　　)

A.10.5 m B.7.5 m

C.12 m D.8 m

4.如图,一架梯子AB长2.5米,顶端A靠在墙AC上,这时梯子底端B与墙脚C的距离为0.7米,如果梯子滑动后停在DE的位置,测得BD长为0.8米,则梯子顶端A下滑了(　　)

A.0.4米 B.0.3米

C.0.5米 D.0.2米

知识点2 最短距离的计算

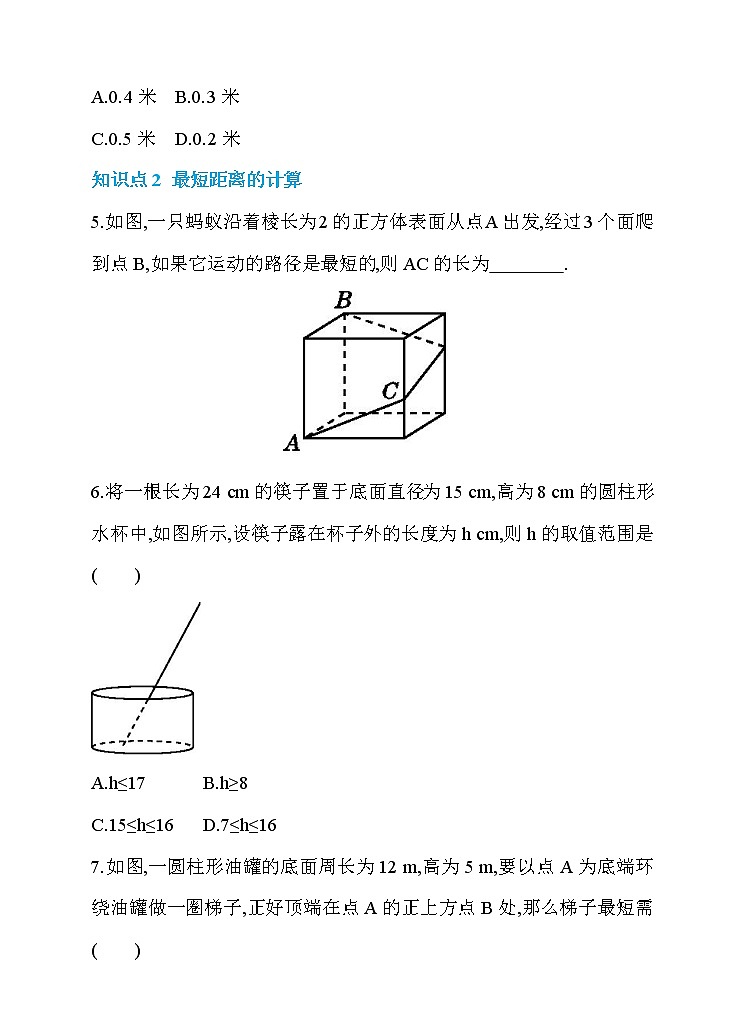
5.如图,一只蚂蚁沿着棱长为2的正方体表面从点A出发,经过3个面爬到点B,如果它运动的路径是最短的,则AC的长为　　　　. 

6.将一根长为24 cm的筷子置于底面直径为15 cm,高为8 cm的圆柱形水杯中,如图所示,设筷子露在杯子外的长度为h cm,则h的取值范围是(　　)

A.h≤17    B.h≥8

C.15≤h≤16 D.7≤h≤16

7.如图,一圆柱形油罐的底面周长为12 m,高为5 m,要以点A为底端环绕油罐做一圈梯子,正好顶端在点A的正上方点B处,那么梯子最短需(　　)

A.17 m B.7 m    C.13 m D.12 m

易错点 求最短路径时对立体图形展开情况考虑不全面导致错解

8.如图,正四棱柱的底面边长为5 cm,侧棱长为8 cm,一只蚂蚁欲从正四棱柱底面上的顶点A沿棱柱的表面爬到点C'处吃食物,那么它需要爬行的最短路程是多少?

提升训练

考查角度1 利用勾股定理借助水中物体变化情况求水深

9.在波平如镜的湖面上,有一朵盛开的美丽的红莲,它高出水面3尺(如图).突然一阵大风吹过,红莲被吹至一边,花朵刚好齐及水面,如果知道红莲移动的水平距离为6尺,请问水深多少?

考查角度2 利用勾股定理借助等距变化求树高(方程思想)

10.如图,在一棵树的10 m高的B处有两只猴子,其中一只猴子爬下树,走到离树20 m处的池塘A处,另一只猴子爬到树顶D后直接跃向池塘A处(假设它经过的路线为直线),如果两只猴子所经过的路程相等,求这棵树的高.

探究培优

拔尖角度1 利用勾股定理解答实际生活中综合应用问题

11.如图,公路MN和公路PQ在点P处交汇,且∠QPN=30°.点A处有一所中学,AP=160 m.假设一拖拉机在公路MN上沿PN方向行驶,周围100 m以内(包括100 m)会受到噪音的影响.

(1)该学校是否会受到噪音的影响?请说明理由.

(2)若受影响,已知拖拉机的速度为18 km/h,则学校受到影响的时间有多长?

拔尖角度2 利用勾股定理解最短距离问题(对称法)

12.如图,A,B两村在河边CD的同侧,两村到河边的距离分别为AC=1 km,BD=3 km,且CD=3 km.现要在河边CD上建一水厂向A,B两村输送自来水,铺设水管的工程费用为每千米2 000元.请你在CD上选择水厂位置O,使铺设水管的费用最省,并求出此时铺设水管的总费用.

参考答案

1.【答案】D　

解：由题意可得∠B=30°,AP=30海里,∠APB=90°,

故AB=2AP=60海里,

则此时轮船所在的位置B处与灯塔P之间的距离为BP==30海里.

故选D.

2.【答案】B　

解：=10(米),∴小鸟至少飞行10米.

3.【答案】C

4.A　

解：在Rt△ABC中,AC===2.4(米),在Rt△CDE中,CE====2(米),∴AE=AC-CE=2.4-2=0.4(米).

5.　解：沿过点A的侧棱将正方体的侧面展开,如图.AB==2,∴AC=.

6.【答案】D　

解：设筷子在杯子中的最大长度为a cm,则由a2=152+82=289=172,得a=17,易知筷子在杯子中的最短长度为8 cm,则筷子露在杯子外面的长度h cm的范围为24-17≤h≤24-8,即7≤h≤16,故选D.

7.【答案】C

8.解:(1)沿棱A'B'将上底面A'B'C'D'和侧面A'ABB'展开,如图①,连接AC'.

在Rt△ABC'中,AB=5,BC'=BB'+B'C'=8+5=13,由勾股定理,得

AC'2=AB2+BC'2=52+132=194,

∴AC'=.

 (2)沿侧棱BB'将侧面A'ABB'和侧面B'BCC'展开,如图②,连接AC'.

在Rt△ACC'中,AC=AB+BC=5+5=10,CC'=8,由勾股定理,得

AC'2=AC2+CC'2=102+82=164,

∴AC'==2.

∵>=2,

∴蚂蚁需要爬行的最短路程是2 cm.

解：在将空间图形中最短路程问题转化为平面图形来解决的同时,还必须全方位考虑各种可能情况,只有这样才能得到正确的答案.

9.解:设水深h尺.如图,在Rt△ABC中,AB=h尺,AC=(h+3)尺,BC=6尺.由勾股定理得AC2=AB2+BC2,即(h+3)2=h2+62.解得h=4.5.所以水深4.5尺.

10.解:设BD=x m,由题意知BC+AC=BD+AD,

∴AD=(30-x)m,

∴(10+x)2+202=(30-x)2,解得x=5,

∴x+10=15,即这棵树高15 m.

11.分析:如图,过点A作AB⊥PN于点B,根据垂线段最短可知若AB>100 m,则不受影响;若AB≤100 m,则受影响.若受影响,则首先需要找出受影响时拖拉机行驶的路段,再构建直角三角形并利用勾股定理求出该路段的长,进而可求出受影响的时间.

解:(1)如图,过点A作AB⊥PN,垂足为点B,则有∠ABP=90°.　

∵AP=160 m,∠QPN=30°,

∴AB=AP=×160=80(m).

∵80 m<100 m,

∴学校会受到噪音的影响.

(2)如图,以A为圆心,100 m为半径作弧,交PN于点C,D(C,D分别在BP,BN上),连接AC,AD.

即当拖拉机在公路MN上沿PN方向行驶到点C处时,学校开始受到噪音的影响,直到拖拉机行驶到点D以外时,学校才不受拖拉机噪音的影响.

在Rt△ABC中,由勾股定理,得

BC2=AC2-AB2=1002-802=3 600.　

∴BC==60(m).

同理BD=60 m.

∴CD=BC+BD=60+60=120(m).　

∴学校受噪音影响的时间为(120÷1 000)÷18=(h)=24(s).

12.分析:铺设水管的费用与水管的长有关,所以本题的关键是使点O到点A,

B的距离之和最小.此时可考虑作点A关于CD的对称点,根据“两点之间线段最短”先确定点O的位置,再利用勾股定理进行求解.

解:如图所示,作点A关于CD的对称点A',连接A'B交CD于点O,则点O即为水厂的位置.连接AO,过点A'作A'E⊥BD交BD的延长线于点E,则A'E=CD=3 km,DE=A'C=AC=1 km.

∴BE=BD+DE=3+1=4(km).　

在Rt△A'EB中,A'B===5(km).　

∴OA+OB=OA'+OB=A'B=5 km.

∴总费用为5×2 000=10 000(元).