北师大版七年级上册1.2 展开与折叠集体备课课件ppt

这是一份北师大版七年级上册1.2 展开与折叠集体备课课件ppt，共25页。PPT课件主要包含了答案显示，一一一相等，两一两相等，见习题，答案B，答案D，①②③等内容，欢迎下载使用。

1．圆柱的展开图是由______个圆和______个长方形组成的；直棱柱的展开图是由________个多边形和若干个长方形组成的，且长方形的个数与多边形的边数________．
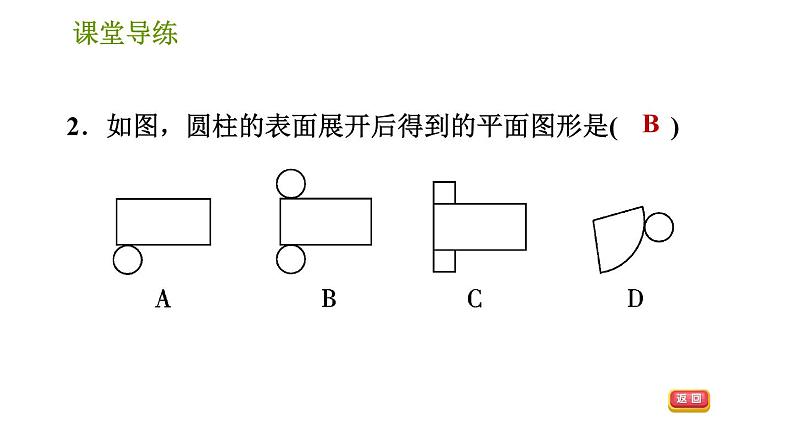
2．如图，圆柱的表面展开后得到的平面图形是(　　)
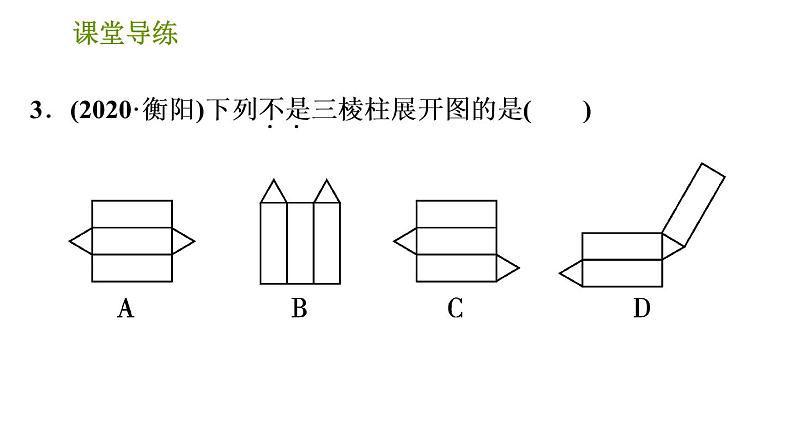
【点拨】A，C，D中三个长方形能围成三棱柱的侧面，两个三角形围成三棱柱的上、下两底面，故均能围成三棱柱，均是三棱柱的展开图．B围成三棱柱时，两个三角形重合为同一底面，而另一底面没有，故B不是三棱柱的展开图．
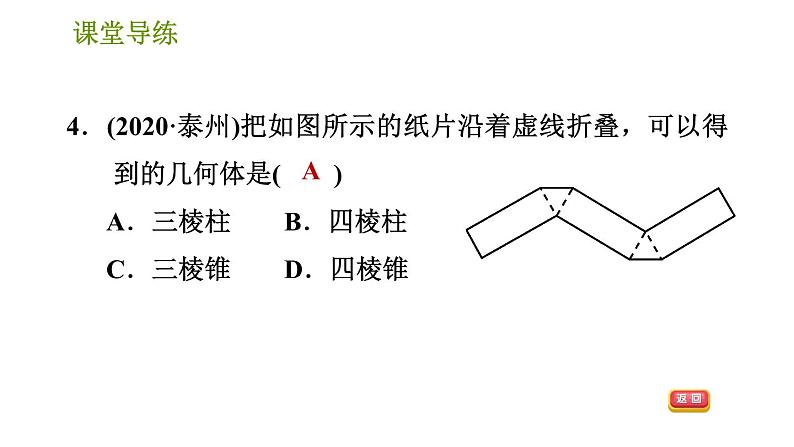
4．(2020·泰州)把如图所示的纸片沿着虚线折叠，可以得到的几何体是(　　) A．三棱柱 B．四棱柱 C．三棱锥 D．四棱锥
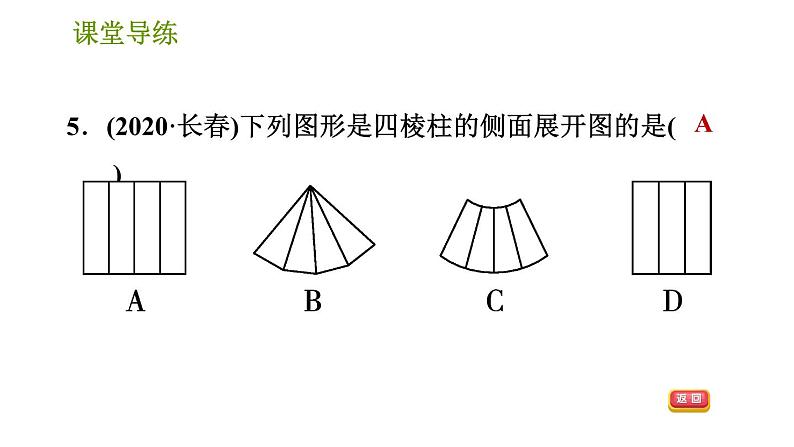
5．(2020·长春)下列图形是四棱柱的侧面展开图的是(　　)
6．(2021·南京金陵汇文学校月考)如图，在长方形ABCD中，AB＝1，BC＝2，把长方形ABCD绕AB所在直线旋转一周，所得圆柱的侧面积为(　　) A．10π B．4π C．2π D．2
【点拨】所得圆柱的底面半径为BC，高为AB，则S侧＝2π·BC·AB＝2π×2×1＝4π.
*7.如图为一直棱柱，其底面是三边长为5，12，13的直角三角形．若下列选项中的图形均由三个长方形与两个直角三角形组合而成，且其中一个为如图所示的直棱柱的展开图，
则根据图形中标示的边长与直角记号判断，此展开图为(　　)
【点拨】A选项中，下方的直角三角形的斜边长为12，不符合题意；B选项中，根据上、下两个直角三角形可知中间长方形水平方向的对边长应为12，不符合题意；C选项中，根据上方的直角三角形可知中间长方形水平方向的对边长为5，根据下方的直角三角形可知中间长方形水平方向的对边长为12，不符合题意；D选项能折叠成一个三棱柱，符合题意．
8．圆锥的展开图是由____个圆和____个扇形组成的；棱锥的展开图是由____个多边形和几个三角形组成的，且三角形的个数与多边形的边数________．
9．(中考·常州)下列图形中，哪一个是圆锥的侧面展开图(　　)
10．(2019·连云港)一个几何体的侧面展开图如图所示，则该几何体的底面是(　　)
*11.(2019·济宁)如图，一个几何体上半部为正四棱锥，下半部为立方体，且有一个面涂有颜色，该几何体的表面展开图是(　　)
【点拨】选项A和C折叠成几何体后涂颜色的面是底面；选项B折叠成几何体后与原几何体的形式相同；选项D不能折叠成封闭的几何体．
12．(1)如图所示的长方体，长、宽、高分别为4，3，6，若将它的表面沿某些棱剪开，展成一个平面图形，则下列图形中，可能是该长方体表面展开图的有__________(填序号)．
(2)图A，B分别是第(1)题中长方体的两种表面展开图，求得图A的周长为52，请你求出图B的周长．
解：图B的周长为6×4＋4×4＋3×6＝24＋16＋18＝58.
(3)第(1)题中长方体的表面展开图还有不少，聪明的你能画出一个周长最大的表面展开图吗？请画出这个表面展开图，并求它的周长．
【点拨】若周长最大，则长为6的棱都剪开．
解：能．如图所示．周长为6×8＋4×4＋3×2＝48＋16＋6＝70.
13．如图是一张铁皮．(1)计算该铁皮的面积．
解：该铁皮的面积为3×1×2＋3×2×2＋2×1×2＝22(dm2)．
(2)该铁皮能否做成一个长方体盒子(底面固定，如图)？若能，画出它的立体图形，并计算它的体积；若不能，请说明理由．
解：该铁皮能做成一个长方体盒子，画立体图形略．该长方体盒子的长为3 dm，宽为2 dm，高为1 dm，所以它的体积为3×2×1＝6(dm3)．
14．(原创题)有两张长9 cm、宽5 cm的长方形硬纸板A，B，如果在A的四个角上各截去一个边长为0.5 cm的正方形，如图①所示；在B的四个角上各截去一个边长为1 cm的正方形，如图②所示．然后把它们分别折叠成一个无盖的长方体小盒，请问哪个硬纸板折叠成的小盒容积较大？为什么？
【思路点拨】根据长方体体积公式计算容积，进行比较即可．注意长方体小盒的长和宽均为长方形硬纸板的长和宽减去2个小正方形的边长，高即为小正方形的边长．