


人教版新课标A选修2-12.2椭圆精品课件ppt
展开1.进一步熟练掌握椭圆的标准方程和几何性质.2.掌握直线和椭圆的位置关系的判断方法,能利用直线和椭圆的位置关系解决相关的弦长,中点弦等问题.
直线与圆的位置关系有相切、相离、相交.判断直线与圆的位置关系有两种方法:(1)几何法:利用圆心到直线的距离d与半径r的关系判断,当d=r时,直线与圆相切;当d>r时,直线与圆相离;当d
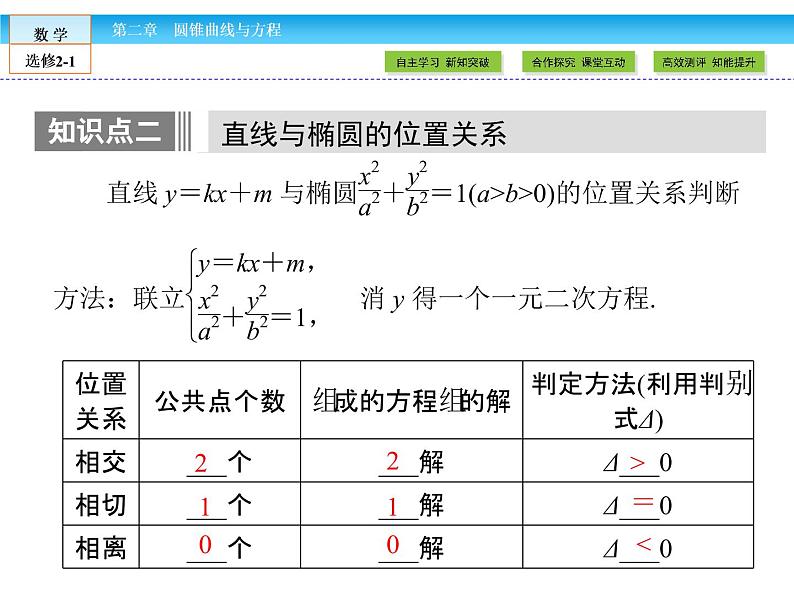
直线与椭圆位置关系及判定方法的理解(1)直线与椭圆有相交、相切和相离三种情况,其位置关系的几何特征分别是直线与椭圆有两个交点、有且只有一个交点、无公共点,并且二者互为充要条件.
(2)判断直线与椭圆的位置关系通常使用代数法而不使用几何法,即先将直线方程与椭圆的方程联立,消去一个未知数y(或x),得到关于x(或y)的一个一元二次方程,由于该一元二次方程有无实数解,有几个与方程组的解的个数相对应,故利用一元二次方程根的判别式Δ,根据Δ>0、Δ=0还是Δ<0即可作出判断.
解析: ∵点(2,3)在椭圆上,∴点(-2,3),(-2,-3),(2,-3)都在椭圆上.故选D.答案: D
当Δ<0,即m>5或m<-5时,直线和椭圆相离.综上所述,当m>5或m<-5时直线与椭圆相离;当m=±5时,直线与椭圆相切;当-5
思路点拨: 由于弦所在直线过定点P(2,1),所以可设出弦所在直线的方程为y-1=k(x-2),与椭圆方程联立,通过中点为P,得出k的值,也可以通过设而不求的思想求直线的斜率.
解析: 方法一:如图,设所求直线的方程为y-1=k(x-2),代入椭圆方程并整理,得(4k2+1)x2-8(2k2-k)x+4(2k-1)2-16=0, (*)设直线与椭圆的交点为A(x1,y1),B(x2,y2),则x1,x2是(*)方程的两个根,
关于中点弦问题,一般采用两种方法解决(1)联立方程组,消元,利用根与系数的关系进行设而不求,从而简化运算.
在解决直线和椭圆的有关问题时,一般是联立方程,消去x(或y)转化为关于y(或x)的一元二次方程.利用根与系数的关系去构造等式或函数关系式,这其中要注意利用根的判别式来确定参数的限制条件.
【错因】 本题错解中误认为当A,B分别为椭圆与x轴的交点时,∠ANB最大,这是错误的,必须通过严密的推导才能得出处于什么样的位置时∠ANB最大.
高中数学2.1曲线与方程优秀ppt课件: 这是一份高中数学2.1曲线与方程优秀ppt课件,共44页。PPT课件主要包含了1曲线与方程,自主学习新知突破,点的坐标,坐标的点,求曲线方程的一般步骤,合作探究课堂互动,曲线与方程的概念,由方程研究曲线的性质,求曲线的方程等内容,欢迎下载使用。
人教版新课标A选修2-12.2椭圆优秀ppt课件: 这是一份人教版新课标A选修2-12.2椭圆优秀ppt课件,共46页。PPT课件主要包含了自主学习新知突破,椭圆的简单几何性质,合作探究课堂互动,求椭圆的离心率等内容,欢迎下载使用。
高中数学人教版新课标A选修2-12.4抛物线一等奖ppt课件: 这是一份高中数学人教版新课标A选修2-12.4抛物线一等奖ppt课件,共37页。PPT课件主要包含了自主学习新知突破,抛物线的几何性质,x≥0y∈R,x≤0y∈R,y≥0x∈R,y≤0x∈R,原点00,合作探究课堂互动,求抛物线的标准方程,抛物线几何性质的应用等内容,欢迎下载使用。













